期中物理总结
一、数学知识
1.1 向量知识
1.2 积分知识
$In=\frac{n-1}{n}I{n-2}$ $I_1=1$ $I_0=\frac{\pi}{2}$
首先要把分界分页的标识符调出来,这样方便排版,方法是“文件—选项—显示—显示所有格式标记”。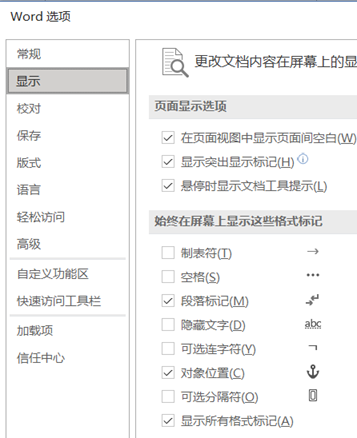
然后明晰一下分节和分页的概念,分节指的是一种文章逻辑上的分割,用这种分割方式分割出的部分,可以具有不同的页眉,页脚,尾注。而对于分页来讲,只是物理层面的分割,一般的应用于比如封面,摘要,目录,参考文献的分割。
分节一般有两种,下一节和连续,理论上来讲,下一节操作等价于连续分节符和分页符,但是在实际操作过程中,下一页分节符会造成空白页的出现,为了避免麻烦,还是用连续分节符为妙。在写冯如杯的论文的时候,分节操作应该在进行其他操作之前做,因为其他操作有可能依赖于分节操作,比如制作目录,参考文献,制作页码页眉等。在这种论文中,一般分为三节,第一节包括封面,中英文摘要,目录,主要原因是区分页码。第二节部分包括正文和参考文献,第三部分是致谢,主要原因是参考文献的尾注引用问题。
采用样式不是必须的,甚至在北航官方提供的文档中,都没有采用样式,而是对字体进行单独的设置。采用样式及一系列操作的原因其实代表着一种设计思想,即动态管理与自动化排版。采用这种思想可以使排版更加有效率,有条理,但是就我个人经验来说,因为冯如杯论文结构较为简单,而自动化排版学习较为复杂,要是时间紧,或者没师傅带,可以不学习这种知识,笔者自己就是因为学的半瓶子醋晃荡,导致了冯如杯差点没有参赛成功,而笔者的好朋友就采用了直接设置的方法,获得了一等奖好成绩。
这篇博文的本质不是一篇答案的汇总,HDLBits的题目组织形式是蕴含思想的(就像五三或者衡中的数学卷子),可以看到,虽然大部分前面的题目都谈不上难,但是如果一道一道的做下来,就会有体会,网站的搭建者是希望通过这组题目,来传递一种硬件设计思想。当然,更谦虚的说法是硬件设计思想基础。这篇博文的目的就是通过这些题目,来勉力阐述这种思想。
我写到了FSM章节的一半,其他的都写了,短期内应该是肝不动了,所以FSM的后面的答案就没有题解了,实在抱歉。
鸣谢名单在结尾放出。因为是无聊的刷题故事(不是为了写这篇文章,我打死都不会写这组题),所以鸣谢人员中只有很少在解决问题上为我提供帮助,但是倒是有很多人陪伴见证了这个无聊的故事,故一并鸣谢。
这篇文章还算成点的东西: