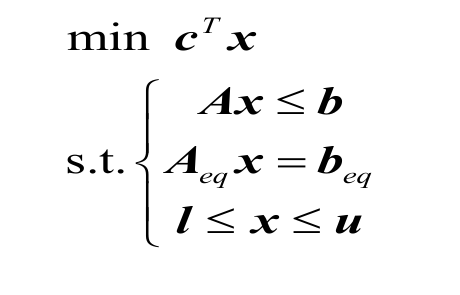钟鼓楼

一、总论

应当意识到，我没有办法依靠平时的积累写出一篇华美的文章。写作或者说表达是必须依靠模板。而 “模板” 的范围不应该只限于语法层面的 “开头，中间段，结尾”。它应当还包括 “语义” 层面，比如说 “意义应当从哪几个角度去答？需要引入事例还是单纯进行说理？” 这样的模板。

还是要感慨一下，英语六级其实和英语能力不太沾边。哪怕是沾边，我也没有办法将其他的英语能力换成成绩。反而言之，即使我的六级成绩不好，但是真的遇到需要英语的场合，也应当坦然积极的准备，而不是自怨自艾，自我否定。

你说这些，跟我有什么关系？

任何失去的东西，都会以另一种形式归来。

我选择的是第一个题目，我会调研 CSDN 问答区、StackOverflow、SegmentFault（思否）三款 IT 问答软件。

一、调研与评测

1.1 问答的意义

朝闻道，夕死足矣。

一、CDQ 分治

因为时间的关系，我也不确定我理解的这个套路是否是所谓的 “CDQ 分治”，还是只是一种具有二维偏序特征的模板。

在这种题目中，我们一般会对于一个二维结构体去排序，比如说

struct Node
{
	int x;
	int y;
};

而且排序一般会发生两次，第一次是在开始前先对某个维度进行一遍排序，然后在分治过程中，利用归并排序的思想，在二分的过程中对于另一个维度再次进行排序。也就是如下模板

一、BFS 模板

如下所示

set<Node> visited;

bool check(Node son);

int bfs(Node start)
{
    // init
    queue<Node> q;
    q.push(start);
    visited.insert(start);
    
    while (!q.empty())
    {
        Node front = q.front();
     	q.pop();
        
        for (son : q.neigbour)
        {
            // prune
            if (check(son))
            {
             	q.push(son);
                visited.insert(son);
                // son is the correct answer
                if (ac(son))
                {
                    return son.info();
                }
            }
        }
    }
    
    return -1;
}

int main()
{
    //...
    int ans = bfs();
    //...
    return 0;
}

其中有几部分需要一一强调，第一个是 check() 函数用于进行减枝，只有经过 check 的子节点会被加入队列。

bool check(Node son);

一、有序和单调

二分本质上是一种更加智能的搜索状态空间的方式，他需要状态空间的状态呈现一种 “有序的一维数组” 的形式，然后再进行搜索。所以一开始的排序是无法避免的。

因为二分的写法问题，所以应当怎样排序也是有一定讲究的，所以排序的时候就可以定义一定的比较方式。

如果更加细致的讨论的话，其实有序只是一个 “小条件”，比如说很多枚举、搜索类的题目的状态空间也是有序的，但是我们却没有用二分法，这是因为其核心是，适用于二分法的题目，它的状态和解之间的关系是单调的，如下所示

一、内积的形式

向量 $X$ 与向量 $Y$ 的内积为

$$X^TY$$

这个时候我们熟悉的转置（准确说是熟悉由陌生，因为转置的意义并不好理解）就出现了。

如果 $X, Y$ 仅仅是坐标，需要在基 $A$ 的作用下发挥作用，那么写出来的效果就更神奇了