大学物理-波粒二象性

所有教材都是按照时间顺序介绍的，但是这样真的是认识量子力学的好方式吗？我觉得不一定，比如说介绍普朗克常量的时候，介绍了一大堆关于热辐射和黑体的概念，其实跟最关键的概念普朗克常量没有很明显的联系。再比如先介绍了波尔的原子模型，但是波尔做的很多理论都是假设，那么这些假设其实都是可以基于薛定谔方程得到推导。所以或许教材组织知识的方式存在一定的问题。

本章最大的阅读问题，就是有很多与量子力学理论体系毫不相干的东西，也必须要学，比如热辐射、光电效应、氢原子光谱。

认为能开发出一套理论，使得所有的东西，包括微观粒子，光子，电磁波都适应，虽然之前我就是这么想波粒二象性的，但是这大概是一种狂妄的表现。所以这篇文章的思路是承认粒子和波有明显的界限，只是波粒二象性使其具有了彼此的一些性质。物质波与波的区别，就好像鲸鱼与鱼区别。

这章主要分为两条线，一条是光的粒子性，包括

热辐射现象，普朗克对黑体辐射的现象做出了自己的量子化解释，进而引入了普朗克常量。
光电效应，爱因斯坦提出光也具有粒子性，应用了普朗克常量
康普顿效应，爱因斯坦光子论的一个应用，至此，粒子性已经全部介绍完毕

另一条线是微观粒子的波动性

从德布罗意天才的构想开始，提出了物质具有波动性，并且给出了如何计算物质波的波长和频率
薛定谔方程利用了德布罗意的思想和公式，提出了奠基公式，薛定谔方程，这个方程可以解出一个波函数，这个波函数就是波动性的体现
不确定性原理，物质波具有了这个本应只在经典波中出现的现象
氢原子的电子：在德布罗意提出物质具有波动性之前，波尔就做出了启发性的假设，解释了氢原子光谱，但是相应的理论不是很完善，在引入薛定谔方程以后，可以得到很好的理论诠释

一、热辐射

1.1 热辐射现象的描述

平衡热辐射：物体辐射出的能量恰好等于同一时间吸收的能量，那么此时物体的温度保持不变，称为平衡热辐射。我们只研究这种情况，是因为这样温度不会对研究造成干扰。相当于研究稳态。

单色辐出度：单位时间内从物体表面单位面积波长为 $\lambda$ 的辐射能，用 $M(\lambda, T)$ 表示，注意，对面积积完分之后，得到的是一个类似于功率的值。

单色吸收比：物体吸收波长为 $\lambda $ 的辐射能与相应波长的入射电磁波能量之比，称为单色吸收比。这里需要明确概念，对于辐射能量，要经过入射 - 吸收 - 辐射的过程，所以我们说平衡热辐射，说的是吸收的能量与辐射的能量相等，而我们说吸收比，说的是入射与吸收的比值，平衡热辐射并没有要求这两者相等。

如果吸收比（应该对应的是所有波长）为1的话，那么我们就得到理想模型黑体，也就是说，黑体可以吸收所有入射的能量。在黑体中，结合平衡热辐射条件，有 入射 = 吸收 = 辐射 。黑体的单色辐出度用 $M_0(\lambda, T)$ 表示。

1.2 黑体辐射实验定律

我们研究的焦点就是绘制 $\lambda - M_0(\lambda, T)$ 图像，注意，在此时，$T$ 只是一个参数，我们的函数关系，是建立在 $\lambda $ 为自变量的基础上的。在这一节，我们会给出两个实验定律

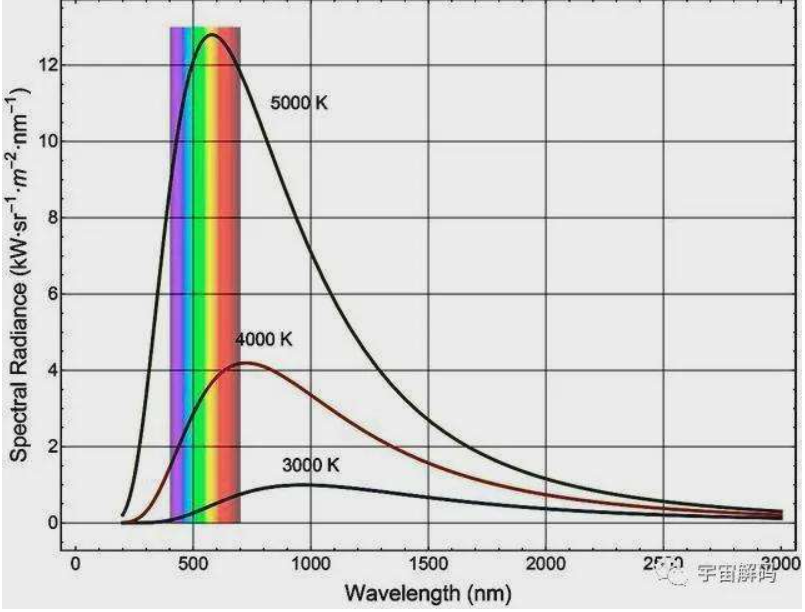
1.2.1 斯特藩-玻尔兹曼定律

每一条曲线下的面积等于黑体在一定温度下的总辐出度，这是一个很显然的事情

$M_0(T) = \int^{\infty}_0 M_0(\lambda, T)d\lambda$

可以看到，当温度升高的时候，曲线下面积明显增大，有

$M_0(T) = \sigma T^4$

这就是斯特藩-玻尔兹曼定律。$\sigma$ 被称为斯特藩常量。

1.2.2 维恩位移定律

每个曲线都都有一个极大值，对应此时的 $\lambda$ 称为 $\lambda_m$ 。

$\lambda_m = \frac b T$

$b$ 被称为维恩常量。

这两个定律反映出热辐射的功率随着温度的升高而迅速增加，而且热辐射的峰值波长，还随着温度的增加而向短波方向移动（没准是因为短波能量高）

1.3 推导 $\lambda - M_0(\lambda, T)$ 函数

前面两个公式只是对图像的性质给出了一些描述，最直接的方法是直接给出图像的函数关系（建立于科学理论，而不是单纯拟合），在经典理论下，有维恩公式和瑞利-金斯公式。但是都拟合的不太好

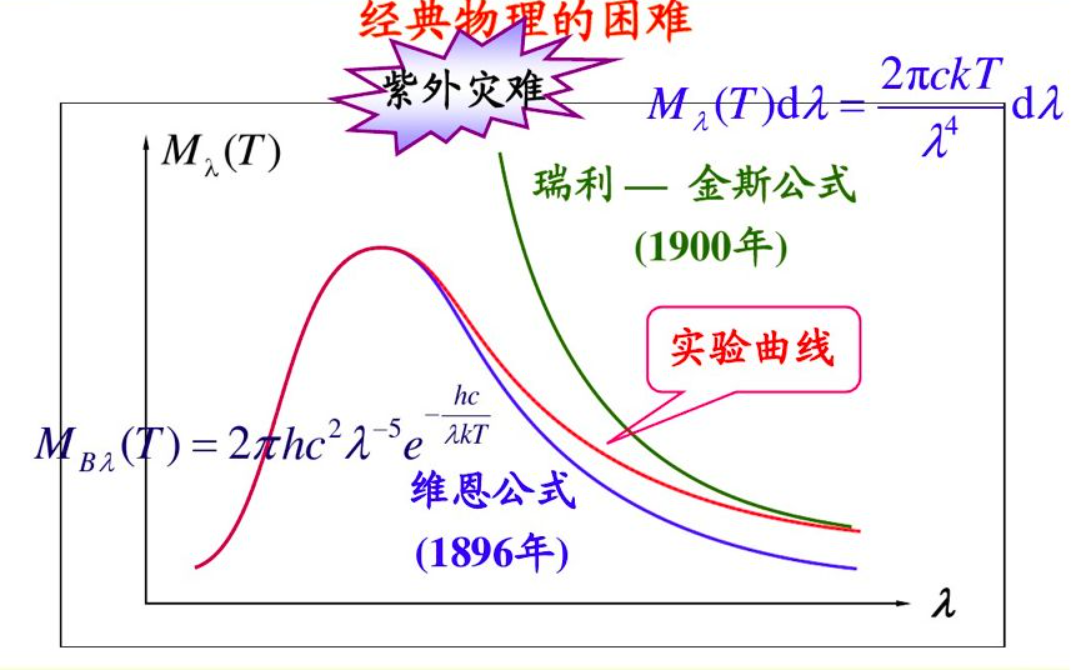
维恩公式长得有点像泊松分布，它模拟出了凸包的形状，但是在长波区衰减的太快。瑞利-金斯公式是一个负幂次函数，所以在短波区会趋于无穷，这被称为紫外灾难。

后来普朗克利用内插法将两个公式衔接了起来获得了正确的公式

$M_0(\lambda, T) = 2\pi c^2 \lambda^{-5} \frac{1}{e^{hc/\lambda kT}-1}$

可以看到形式还是很像维恩公式的，但是内插法不是理论，这个正确的函数关系需要理论的支持，也就是我们熟悉的

$\epsilon = h\nu$

从这个公式开始，我们的噩梦开始了。

二、光子论

2.1 光电效应

因为高中已经学的很熟练了，所以就不耽误时间写了，唯一有一点需要补充的就是计算光子的质量和动量

当计算质量的时候，有

$m_{\phi} = \frac{\epsilon}{c^2} = \frac{h\nu}{c^2}$

当计算动量的时候，有

$p = m_{\phi}c = \frac{h\nu}{c} = \frac{h}{\lambda}$

可以看到，在动量的推导中，用到了 $c = \lambda \nu$ 这个条件，但是在物质波中，这个条件没准是不成立的（就算成立，成立的也不太自然）。但是物质波中计算波长依然可以用这个式子。

2.2 康普顿效应

2.2.1 实验现象

就是说有一个摄谱仪在旋转，然后当旋转到特定的角度的是时候，会发现有一个波长对应的射线的强度特别大。

康普顿认为，是当 X 射线光子与原子外层电子发生碰撞的时候，由于外层电子与原子核束缚较弱，这些电子可以看为“自由电子”，当光子与这些电子碰撞时，自由电子吸收一个入射光子后发射一个波长较长的光子。注意，这里是吸收整个光子后再发射出一个波长较长的光子，此间是两个光子，没有违背光子不可分割的理论。

2.2.2 理论推导

可以看做遵循能量守恒和动量守恒定律。

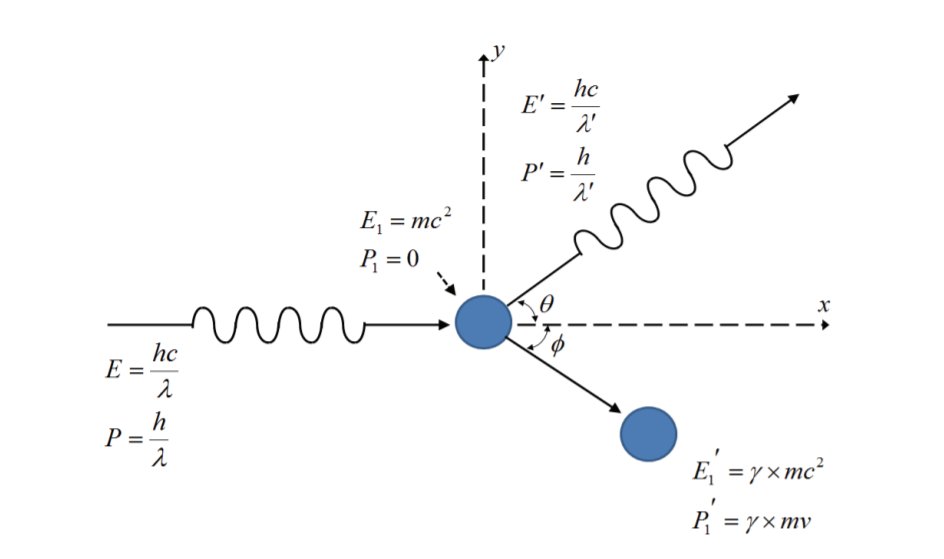
根据能量守恒，有

$h\nu_0 + m_0 c^2 = h\nu + mc^2$

其中 $m_0$ 是电子的静质量。

根据动量守恒，在 x 方向上有

$\frac{h\nu_0}{c} = \frac{h\nu}{c}\cos \phi + mv\cos\theta$

在 y 方向上有

$0 = \frac{h\nu}{c}\sin\phi - mv\sin\theta$

最终可以解得

$\Delta \lambda = \lambda - \lambda_0 = \frac{2h}{m_0c}\sin^2\frac{\phi}{2} = 2\lambda_C\sin^2\frac{\phi}{2}$

其中 $\lambda_C = \frac{h}{m_0c}$ 被称为康普顿波长，在这道题里面没有实际意义。在其他的问题中，认为是测量粒子位置的基本限制，这里不做详细说明。

三、物质波

3.1 总论

物质波说的是实物粒子表现出了波动性的现象，这种波动性最后被解释为了概率波，概率波说的是事物可以在空间的任何地方出现，只不过需要服从一定的概率分布，而这种概率分布恰好表现出波的特性，所以我们说它是波，严格的讲，鲸鱼不是鱼，物质波不是波，我觉得太过于统一波粒二象性没啥好处，波粒二象性不是我用来混淆波和粒子的工具。

正是因为物质波不是经典波，所以我们并不要求物质波具有波的一切特性，比如是说可以算波速（反正以我的学识，不觉得物质波如果加入波速以后体系还能自洽）。我们用的比较多的，就是干涉和不确定性原理（都不需要波速）。

如果反过来说，我是不是也把光的粒子性看得太重了，因为如果太重的话，会跟光的波动性矛盾，只是之前我没有想过这个问题（也是因为对波的认识不多，所以矛盾不突出），毕竟一个弥散在空间中的波，是怎样变成一个粒子的呢？是很让人头疼的事情。我记得我之前看过一个说法，是光只有在传递能量的时候表现出粒子性，这个说法无论对错，度很好。

3.2 波函数

微观粒子运动的图景是这样的：粒子会出现在任何地方，也就是说，出现在哪个位置是一个概率问题，而这个概率问题，刚好可以用一个余弦函数来描述，这就是波函数的意义。这是第一个有趣的事情，而另一个巧合的事情是，这个余弦函数的参数，比如说频率，波长，恰好可以用德布罗意的理论计算出来：

$\lambda = \frac{h}{p} ,\quad\quad\quad\quad\nu = \frac{E}{h}$

但是还是要再次强调，我们只是恰好这样的，而不是说物质就是波了。我们不能基于得到频率和波长，做出其他有效推断。

然后我们就会写出一个波函数，大概就是这个样子

$\Psi(x, t) = \Psi_0 e^{-i\frac{2\pi}{h}(Et - px)}$

其实这个式子就是个安慰剂，以后我们根本不会用到它，具体原因下一节解释。

关键是我们有了波函数的表示符号 $\Psi$ ，这个式子的作用理论支持是在某个时间某一地点出现的概率正比于波函数与其共轭复数的成绩。

$\mid\Psi\mid^2 = \Psi\Psi^*$

表示在某一时刻在某点处单位体积内粒子出现的概率，称为概率密度。也就是说，我们为了研究微观粒子的位置，就需要求解概率，而求解概率就需要求解波函数。当波函数给定的时候，我们对粒子已经有了很好的掌控。

3.3 薛定谔方程

上面已经总结出我们研究微观粒子的核心目的，就是求解波函数。其实我们已经给出了一种方法，那么就是给出粒子的动量和能量，然后根据德布罗意的两个方程，计算出波函数的频率和波长，波函数也就定下来了，但是我们并没有采用这种方法。这是因为实际上（我自己起码是这样理解的），我们没办法确定一个微观粒子的动量和能量（因为不确定性原理）。这就导致了一个很直接的后果，波函数对我们来说，就是一个参数没有任何物理意义的函数，我们必须开发其他方法来求解这个波函数。

这个方法就是薛定谔方程。写成这样，其中 $U$ 是势能，$\hbar = \frac{h}{2\pi}$ 是约化普朗克常量。

$-\frac{\hbar^2}{2m}\nabla^2\Psi + U\Psi = i\hbar\frac{\partial \Psi}{\partial t}$

首先需要强调的是，薛定谔方程的地位跟牛顿力学三大定律是相似的，它是不需要证明的，只有以它为原理推导其他公式。

其次分析一下这个方程的结构，有如下特征：

它求解出来是一组波函数，这个波函数是一个复函数
这是一个二阶偏微方程，我们是没有办法在只学了数分的基础上求解的，反正我不会解
在这个式子中，参数有粒子的质量和势能，这两个量都是相对较好获得的
这个式子其实给出了，只要个给定了环境和粒子，也就是情景，那么理论上就是可解的。这么看，除了结构复杂一些，其中的思路跟牛二给定了受力情况，就知道了一切的思路相仿。
解出的这组波函数，必须满足归一化、边界条件等多个约束，这是造成分立的原因

正如上面的第二个特征，这个方程我们是解不了的，所以我们需要弱化一下条件，让其变成我们可以求解的状态。我们不能求解的原因在于里面是偏微分的，我们对 $x,y,z,t$ 都做了微分，所以我们不会了，所以为了让其转成我们会的微分方程，必须将微分量从4个减少至1个，那么如果限制运动为1维运动，那么 $y,z$ 就可以去掉了，那么如果再把 $t$ 去掉，就变成我们可以求的样子了。

这时我们再对求解的情景加一个条件势能只是坐标的函数，那么经过繁复的数学推导，我们就可以得到定态薛定谔方程，写作

$-\frac{\hbar^2}{2m}\nabla^2\psi + (U-E)\psi = 0$

这个方程同样有很多特征：

$\Psi = \psi e^{-\frac{i}{\bar{h}}Et}$ ，其中 $\psi$ 只是位置的函数，我们方程求解的对象由 $\Psi$ 变成了 $\psi$， $\psi$ 被称为空间坐标函数
$E$ 只是一个我们设出来的参数，也就是说，我们解出来的空间坐标函数，里面会有 $E$ 这个参量。 $E$ 这个参量，我觉得，只是设出来的，虽然具有能量的量纲，但是是没有实际意义的，但是看上去后面的应用中，好像 $E$ 拥有了粒子能量的物理意义，所以就马马虎虎吧。此外，$E$ 也是会受到归一化、边界条件等多个约束，导致分立。
$E$ 的取值会确定对应的 $\psi$。换句话说，当我们解出了一个确定的 $\psi$，我们同时也用了一个确定的 $E$ 。再说的明确写，我们不仅解出了例子的位置概率，还解出了此时粒子的能量。我们解出来的东西多了。
计算概率的时候，有 $\mid\Psi\mid^2 = \Psi\Psi^{*} = \mid\psi\mid^2 e^{-\frac{i}{\hbar{}}Et} e^{+\frac{i}{\hbar{}}Et} = \mid\psi\mid^2$，所以计算概率的时候，直接使用 $\psi$ 就好了。
如果 $E - U$ 是正数，那么才能解出一个三角函数，不然解出来就应该是一个指数函数了。从这个角度看，好像把 $\Psi$ 叫做波函数有点局限性了，比如说在势垒，如果出现隧道效应，粒子在势垒中应该就不是三角函数。

如果我们只要将研究局限于一维定态，那么薛定谔方程对我们来说就是一个二阶常系数微分方程，就是可解的。

3.4 不确定性原理

不确定性原理并非是物质波的特有现象，而是说，所有的波都是具有这个特征的。我们强调的是，物质波原来像经典的波一样，是具有不确定性的。

对于经典波，其不确定性体现在频率和测量时间的不可得兼。这个可以由傅里叶变换很好的体现，因为我也不会，就放两张图吧：

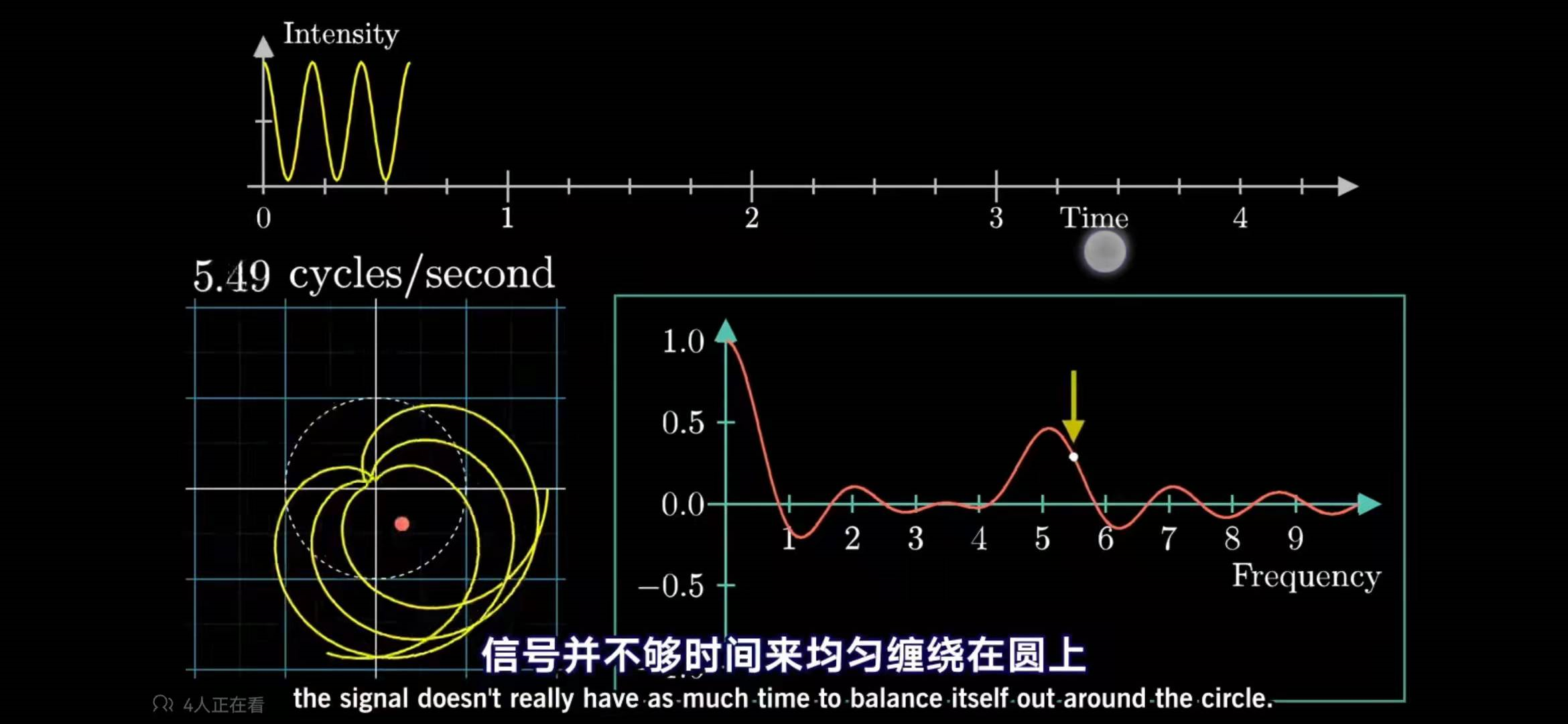
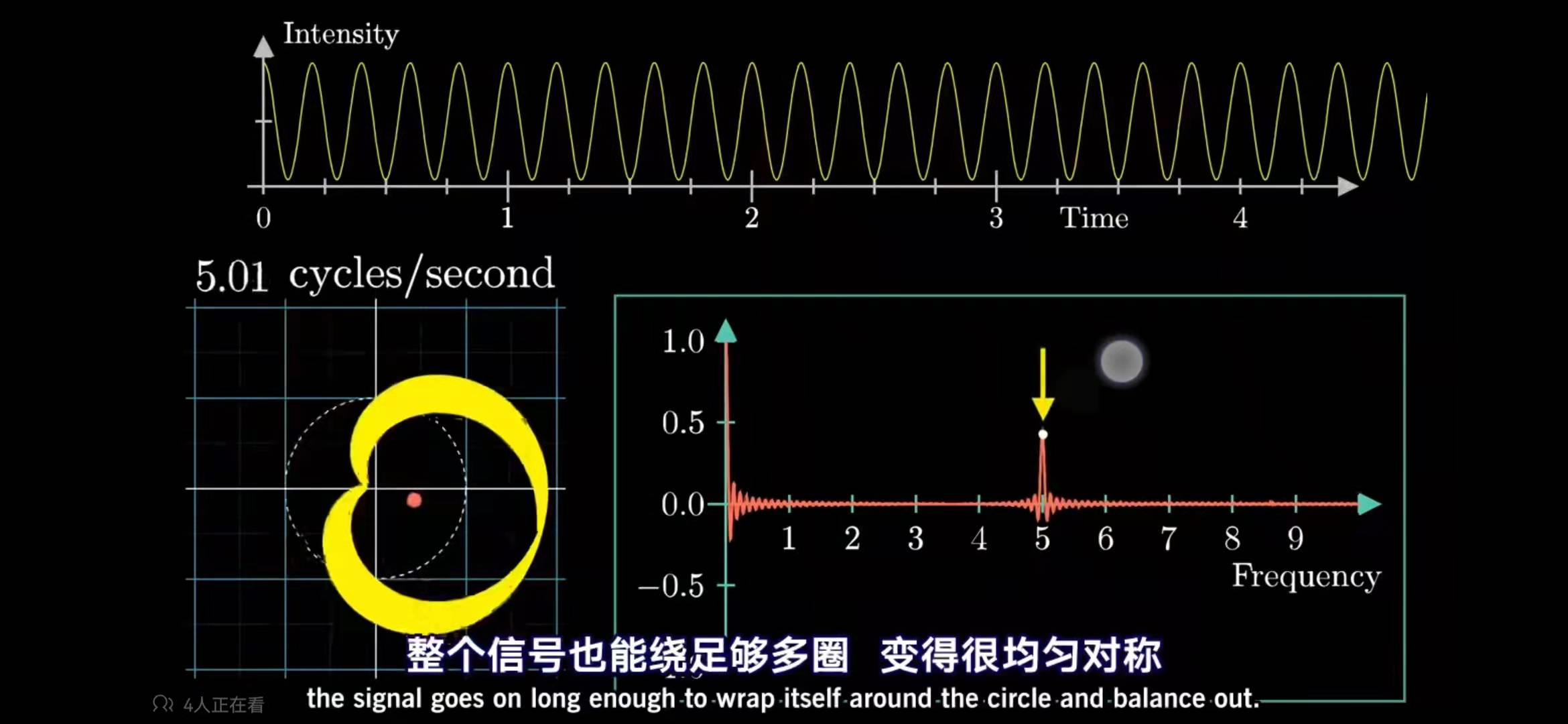
可以看到，当测量时间短的时候，那么频率对应的范围就会变大，换句话说，频率就测不准了，而当频率测得很准确的时候，测量时间就会变得很长。

众所周知，频率与能量对应，所以有一个不确定原理还挺好理解的

$\Delta E\Delta t\geq \frac{\hbar}{2}$

另一个不确定原理在视频中也给出了解释，应该是应用了相对论，所以我就放弃了，所以记录下来就好了

$\Delta x\Delta P_x \geq \frac{\hbar}{2}$

可以看到，一旦位置偏差大，那么相应的动量偏差就会减少，而动量偏差大的时候，位置就很确定。这种不确定关系并不是由测量造成的，而是物质本身的性质。

3.5 薛定谔方程应用

3.5.1 一维无限深势阱

都是一些无聊的数学推导，在这里摆上结论

$\Psi(x, t) = \sqrt{\frac{2}{a}}\sin(\frac{n\pi}{a}x)e^{-i\frac{E}{\hbar}t}$ $E_n = \frac{n^2\pi^2\hbar^2}{2m^2}$

其中 $a$ 是势阱的宽度。唯一需要强调的就是粒子的物质波在阱中形成驻波。

第一个式子很有意思，因为如果将其看为驻波的话，因为驻波的形式是

$y = 2A\cos(\frac{2\pi}{\lambda}x)\cos\frac{2\pi}{T}t$

可以看到空间角频率是 $\frac{n}{2a}$ 此时对应的波长满足 $a = n\frac{\lambda}2$ 。刚好是驻波的条件，而后面的 $\frac{E}{\hbar} = 2\pi\nu$ 刚好是角频率。

当然，还有一种更有意思而且更直观的理解，是这样的：一维无限深势阱中的粒子的波函数，在边界处为0，这种定态物质波相当于两端固定的弦中的驻波，因而势阱宽度 $a$ 必须等于德布罗意波半波长的整数倍，也就是说有如下等式成立

$p = \frac{h}{\lambda},\quad a = \frac{n\lambda}{2},\quad E_n = \frac{p_n^2}{2m}$

用这三个式子就可以解出来：

$E_n = \frac{n^2h^2}{8ma^2}$

3.5.2 一维势垒

这个连波函数都没有给出来，可能因为解出来就不是个三角函数吧（我不确定）。

在粒子总能量低于势垒壁高（$E<U_0$）的情况下，粒子有一定概率穿透势垒。粒子能穿透比其他动能更高的势垒的现象，称为隧道效应。通常用贯穿系数表示粒子贯穿势垒的概率

$T = Ce^{-a\frac{2}{\bar{h}}\sqrt{2m(U_0 -E)}}$

可以看出，粒子的质量越小，势垒越窄，粒子的能量与势垒的高度差越小，穿透概率越大。

3.5.3 氢原子问题

3.5.3.1 实验定律

里德伯方程

$\frac{1}{\lambda} = R(\frac{1}{k^2} - \frac{1}{n^2})$

其中的 $R$ 是里德伯常量。如果将 k 置 2 ，就得到了巴尔末公式。

3.5.3.2 薛定谔方程解氢原子问题

因为不再是一维问题，所以我们是没有能力求解的，所以只有结论，主旨就是原子内电子的状态由四个量子数确定。

能量量子化，其中 $n$ 被称为主量子数，其中 $n$ 的取值是从 1 开始的，这个公式太难背了，所以还是记住 $E_1 = -13.6eV$ 吧。
$E_n = -\frac{me^4}{8\varepsilon_0^2 h^2}\frac{1}{n^2}$
轨道角动量量子化，决定了电子云的形状，其中 $l$ 称为角量子数
$L = \sqrt{l(l+1)}\hbar$
其中 $l$ 的取值是从0到（n - 1），也就是说，一共有 n 个形状
轨道角动量空间量子化，决定了电子云的方向，其中 $m_l$ 称为磁量子数
$L_z = m_l\hbar$
其中 $m_l$ 的取值是 $0,\pm1,\cdots,\pm l$。也就是说，一个确定了角量子数的电子，最多有 $2l + 1$ 种取向。我觉得更直观的是求夹角，有
$\theta_z = \arccos(\frac{L_z}{L}) = \arccos(\frac{m_l}{\sqrt{l(l+1)}})$
空间取向量子化，自旋磁量子数 $m_s$ ，取值 $\pm\frac{1}{2}$，此外有公式
$S = \sqrt{\frac{3}{4}}\hbar,\quad S_z = \pm\frac12 \hbar$
其中 $S$ 是电子的自旋角动量，$S_z$ 是其在外磁场方向上的分量。

3.5.3.3 能量最小原理

这是偶尔看到的，高中的时候不知道，能级的高低以 $(n + 0.7l)$ 的值来取定，该值越大，那么能级越高。