应该说,我们去看随机过程的时候,具有两条线索,一条是纵向来看,即给定事件 $e_0$ ,获得的是样本函数;另一条是横向来看,即给定参数 $t_1$ ,获得是在 $t_1$ 时刻的一个随机变量。我觉得随机变量比较好理解。但是我同时也觉得,对于样本函数要是能有一个更加深入的理解,那么对随机过程的理解才能更上一层楼。
我觉得,样本函数也可以看做一个特殊的随机变量。随机变量的观测值本来应该是一个实数,但是我们的随机过程的观测结果是一个函数,也可以理解为一个过程。
我在做题的时候,还是横切应用的多一些,比方说分析数字特征的时候,自相关函数和自协方差函数都是选定了 $t_1,t_2$ 类似于选定了两个横切面研究性质。但是话还没说满,感觉还有进一步理解的可能,比如没有给定 $t_1,t_2$ 的值。
或许达到一种 “涵虚混太清” 的感觉才是正解。有言道:“随机过程随机过,实变函数学十遍,计组原理成组寄,汇编语言不会编。”
一、随机过程总论
1.1 直观理解
我找到一段话,用来从纵切的角度解释随机过程,我觉得非常有道理:
自然界中事物的变化过程可以大致分成为两类。一类是其 变化过程具有确定的形式,或者说具有必然的变化规律,用 数学语言来说,其变化过程可以用一个或几个时间t的确定函数来描述,这类过程称为确定性过程。例如,电容器通过电阻放电时,电容两端的电位差随时间的变化就是一个确定性函数。而另一类过程没有确定的变化形式,也就是说,每次对它的测量结果没有一个确定的变化规律,用数学语言来说, 这类事物变化的过程不可能用一个或几个时间t的确定函数来描述,这类过程称为随机过程。
下面它给出了一个例子:
设有n台性能完全相同的接收机。我们在相同的工作环境和测试条件下记录各台接收机的输出噪声波形(这也可以理解为对一台接收机在一段时间内持续地进行n次观测)。测试结果将表明,尽管设备和测试条件相同,记录的n条曲线中找不到两个完全相同的波形。这就是说,接收机输出的噪声电压随 时间的变化是不可预知的,因而它是一个随机过程。
我觉得上面的话很好的体现了纵切的特点,我们用图再加深一下理解:
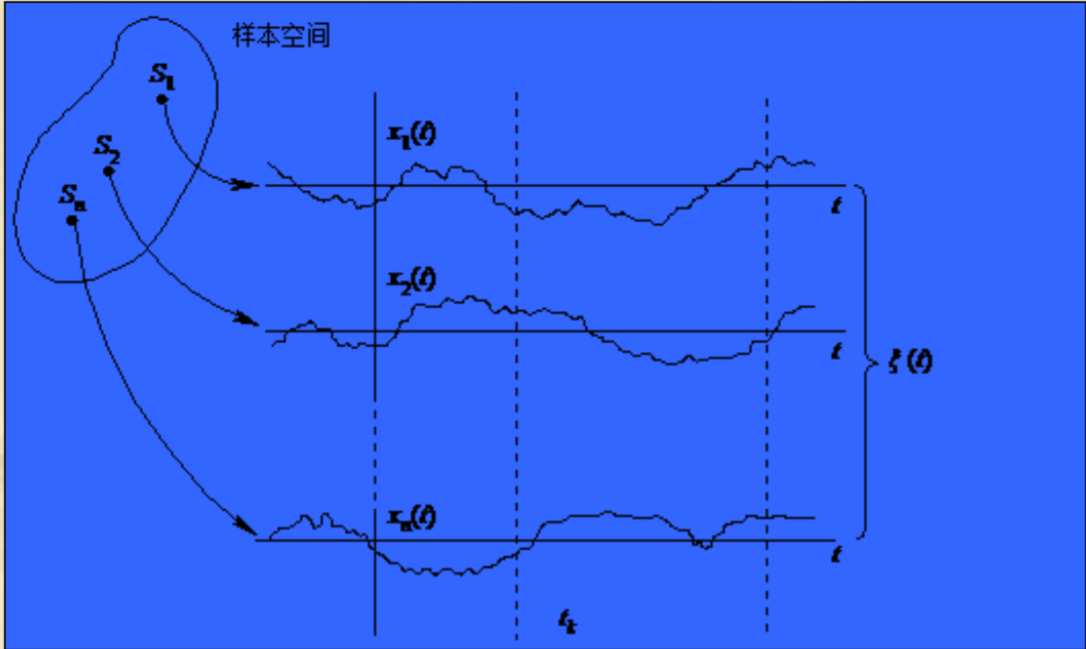
可以视为,每次取样,观测结果都是一个过程,而这个过程具有随机性。
1.2 基本概念
对于样本空间中的每个 $e_0$ ,$X(e_0,t)=x(t)$ 是仅依赖于 $t$ 的函数(注意这里是小写,说明是观测结果),称为随机过程的样本函数,它是随机过程的一次物理实现或对应 $e_0$ 的轨道。
对于任意给定的参数集中的 $t_1$ ,$X(e,t_1) = X(t_1)$ 是一个随机变量(注意这里是大写,说明依然是一个随机变量),称为随机过程在 $t = t_1$ 时的状态变量,简称状态。这个用的确实多,在后面马尔科夫链的讨论中,这个也是一个很基本的概念。
函数值集合 ${X(e, t) \mid e\in S, t\in T}$ 称为随机过程的状态空间,记作 $S$ 。可以看出,这个概念是基于上面状态的概念提出的。
我们对随机过程进行分类,可以按照随机过程的参数集和状态空间来分类。当 $T$ 是离散的时候,随机过程就是随机变量序列,简称随机序列。一般记为 $X(t_n) = X_n$。这里给出了从随机过程角度理解随机序列的定义。
1.3 概率分布
这个方面我没有理解的太好,所以只能记住了。
称为随机过程 $X(t)$ 的 n 维状态分布。当参数趋于无限的时候,可以完全确定随机过程的统计特征。但是我们显然不能取无数个值,所以我们如果想要完全了解一个随机过程,下面提出了一种独立过程的思路,马尔科夫链的关于状态转移的研究,应该也算一种超越。
如果对任何正整数 $n$ ,随机过程的任意 $n$ 个状态都是都是相互独立的,则称这个过程为独立过程,独立过程的 n 维分布有
对于独立过程,由过程的一维分布函数就能确定该过程的统计特征。
1.4 数字特征
数学期望
这个特别x有意思,是因为输出不再是一个常数,而变成了一个函数,其实挺有意思的,对随机过程取期望,得出的应该还是一个过程,直观地看,表示随机过程的 n 个样本函数曲线的摆动中心。
二阶原点矩
称为随机过程 $X(t)$ 的均方值函数,简称均方值。其实也可以看作在过程中的一个反映。
二阶中心距
称为随机过程 $X(t)$ 的均方差函数,简称均方差。它表示随机过程在时刻 t 对于均值 $\mu_X(t)$ 的偏离程度。 均值和方差都只与随机过程的一维概率密度函数有关,因而它们描述了随机过程在各个孤立时刻的特征。为了描述随机过程在两个不同时刻状态之间的联系,还需利用二维概率密度引入新的数字特征。
自相关函数
自协方差函数
二、平稳过程
关于这个部分,感觉虽然平稳这个词听起来很直观,但是确实这一章很不直观。所以大部分的知识都是记忆,题型感觉也都是利用判定定理去做判定。所以重点在于掌握和记忆各个判定定理,还有简单的性质。
所谓平稳随机过程,是指它的统计特性不随时间的推移而变化。
2.1 严平稳过程
对任意 $t_1,t_2, \cdots, t_n \in T$ ,任意实数 $\epsilon$ ,有 $t_1 + \epsilon,t_2 + \epsilon, \cdots t_n+\epsilon \in T$ ,对任意 n 维分布函数都成立:
则称 $X(t)$ 为严平稳过程。严平稳过程的含义是:过程的任何有限维概率分布与参数 t 的原点选取无关。
严平稳过程的一维分布函数与参数 t 无关,二维分布函数仅依赖于参数间距 $\tau = t_2 - t_1$,与参数本身无关。除此之外,严平稳过程还有如下性质:
- 严平稳过程的 $\mu_X,\Psi_X^2,\sigma_X^2$ 均为常数
- 严平稳过程的 $R_X,C_X$ 均为参数间距 $\tau = t_2 - t_1$ 的函数。
上述的这两条性质又被称为平稳性。但是需要强调的是,这些性质可以用于否定非严平稳过程。但是并不能作为判定定理判定一个随机过程是严平稳过程。能判定是严平稳过程只能用定义,但是定义里“任意”的字样,显然不太好实践,也就是说,我们很难判定一个过程是严平稳过程,所以我们放宽松了条件,以此产生了广义平稳过程的概念。
伯努利序列:独立重复地进行某项试验,每次试验成功的概率为 $p$ ,以 $X_n$ 表示第 $n$ 次实验成功的次数,则 ${X_n}$ 是严平稳过程。
2.2 广义平稳过程
我们判定广义平稳过程就简单的多,只有条件:
- $\Psi^2(t)$ 存在且有限
- $\mu_X$ 是一个常数
- 自相关函数 $R_X$ 仅依赖于 $\tau$
这里详细说一下为什么会有一个不太自然二阶矩存在且有限的条件,这个其实是一种条件的简化,他可以被翻译成“期望和方差都存在且有限”。这是因为我们有广义距离不等式(我自己起的名字)
所以如果二阶矩存在,那么一阶矩就存在,进而方差也存在。这是一个很巧妙的条件化简。
广义平稳过程简称平稳过程,有以下很良好的性质:
自相关函数 $R_X$ 仅依赖于 $\tau$(定义)
$\mu_X,\Psi_X^2,\sigma_X^2$ 均为常数,这是因为
$C_X(t, t+\tau) = R_X(\tau)-\mu_X^2 = C_X(\tau)$ 只与 $\tau$ 有关。
广义平稳过程的实例就很多了,比如说泊松过程、白噪声,通信系统的加密序列。
广义平稳过程不一定是严平稳过程,严平稳过程也不一定是广义平稳过程。存在二阶矩的严平稳过程才必定是广义平稳过程。
2.3 各态遍历性
首先对各态遍历性这个性质由一个直观的认识:它的数字特征(均为统计平均)完全可由随机过程中的任一实现的数字特征(均为时间平均)来替代。也就是说,通过一次试验获得的一个样本函数就可确定过程的数字特征。
尽管我们把遍历过程放在平稳过程这一章去讲,但是并不是所有的平稳过程都是遍历过程。遍历过程具有自己的判定条件,我们首先先介绍几个新的函数:
时间均值
当存在 $\bar{X(t)} = \mu_X$ 的时候,就说 $X(t)$ 的均值具有各态遍历性。
时间相关函数
当存在 $\bar{X(t)X(t + \tau)} = R_X(\tau)$ 的时候,则说 $X(t)$ 的自相关函数具有各态遍历性。
只有同时具有均值和自相关函数的各态遍历性的随机过程,我们才成为该平稳过程是遍历过程。