一、时间复杂度的估计
1.1 三种方法
估算分治问题的时间复杂度一共有三种普遍的方法:
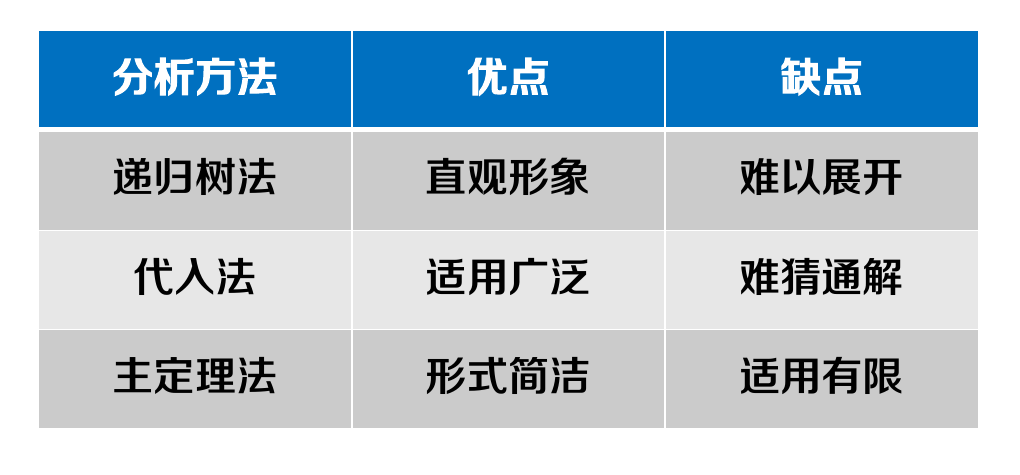
1.2 代入法
代入法需要结合第二数学归纳法使用,使用起来还是很简单的(难点在于猜测),比如估算
可以猜测其上界为 $ O(n\log n) $ 。那么需要检验一下基准情况,对于常数 $c$ ,有
然后进行归纳假设,设当 $k < n$ 时,有 $T(k) < c k \log k$ 。对于 $n$ 有
可以看到,只要稍微控制一下 $c$ ,就可以使得 $T(n) \leq n \log n$ 。归纳成立。
1.3 树方法和主定理
这两者本质是一种方法,其实都是通过计算一个树形结构来获得复杂度,这是因为分治问题本身就是一个树问题。这棵树大致如下
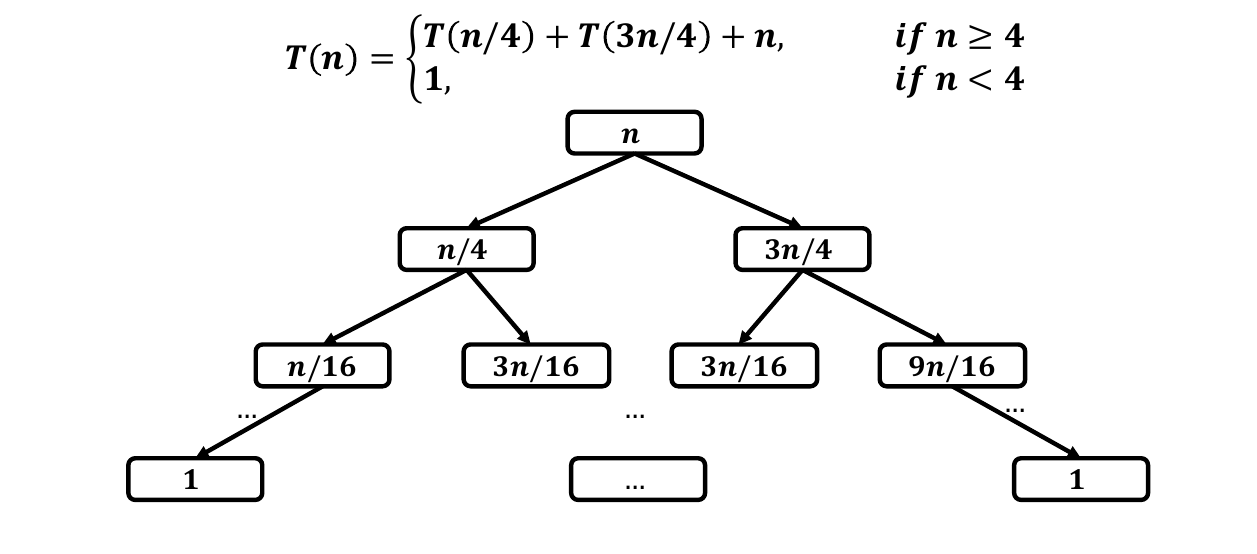
其中非叶子节点记录的是合并的代价(也就是非递归部分的复杂度),而前面的分治则决定了树的结构(一般我们需要的信息是树的高度)。叶子节点记录了基准情况。我们计算的复杂度就是把这棵树所有节点加起来。
主定理是这样的一棵树,它的子树是相同的,不会像上面一样出现不同高度的子树(同一层子树)。这无疑限制了求解的范围。但是给出了统一的数学思路,也就是
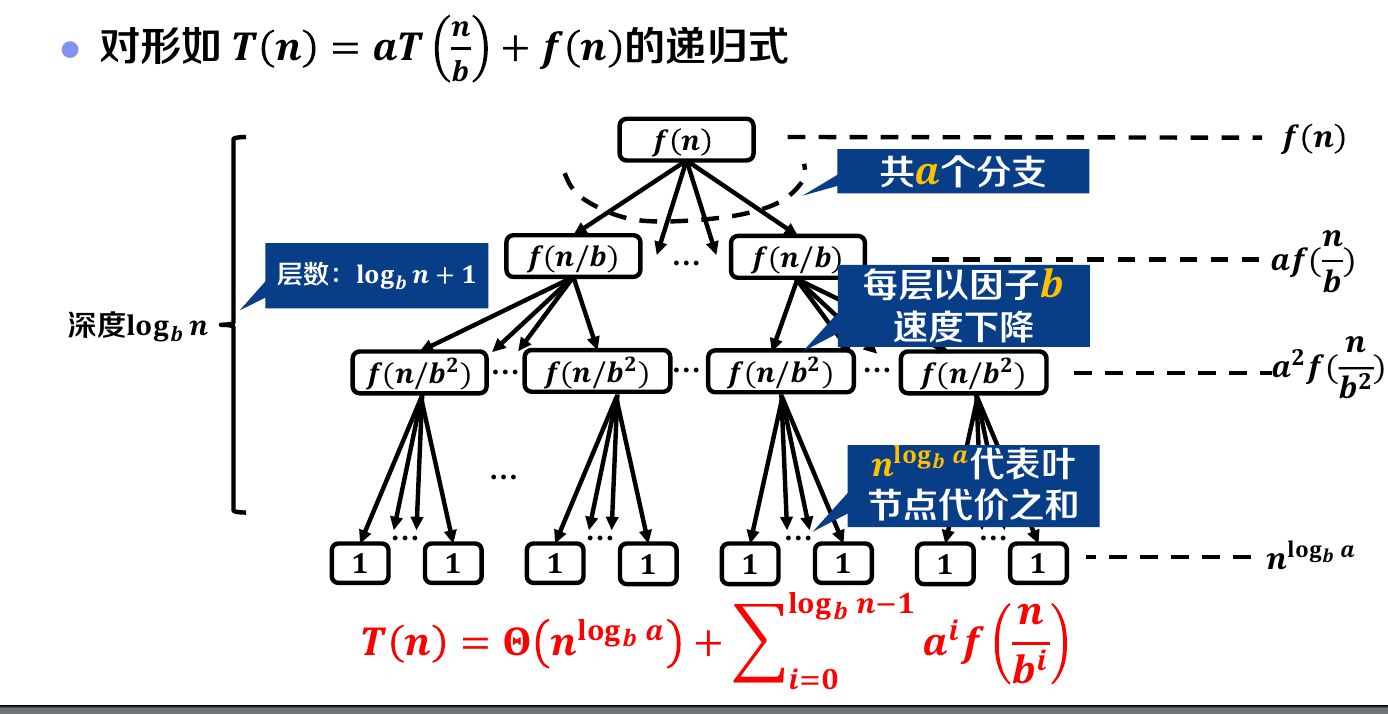
可以看到复杂度由两部分构成,第一部分是叶子节点的代价,第二部分是非叶子节点的代价。问题的难点是对于第二部分的处理。
其实第二部分中,如果 $f(n)$ 是一个幂函数,那么求和就是一个等比数列的求和,是很容易计算的,困难的是非幂函数的情况,我们和树方法一样,都需要面临一个不确定能不能的求和问题。
我们将比较容易求和的部分总结了一下,形成了主定理:
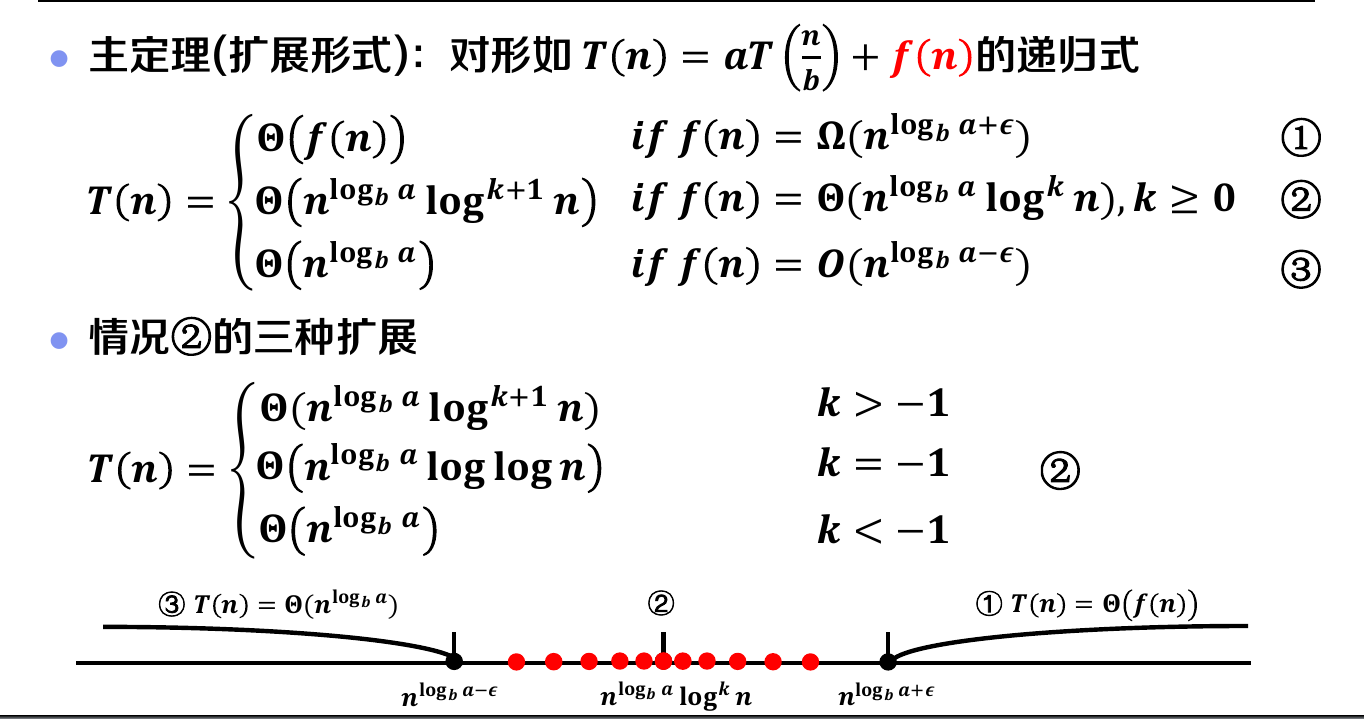
二、平面最近点对
2.1 题目描述
在第一象限有 $n$ 个点对(其实利用平移坐标轴,这个很容易扩展到四象限),求其中距离最近的两个点对。
2.2 分治算法
这道题如果暴力求解,是 $O(n^2)$ 的复杂度,所以如果有巧妙办法(必然有,不然我就不写了),那么应该是更小的时间复杂度。所以我们考虑用分治算法。
从需求出发,我们按照 $x$ 坐标将点分为两组,一半的 $x$ 比较大,另一半比较小。假设我们已经获得了这两个部分的结果,也就是我们知道 $A_1, A_2$ 的解是 $h_1, h_2$ ,那么考虑如何依靠他们来获得最终的答案(即归并过程)。

我们说,最终的结果只可能为 $h_1, h_2$ ,或者是 $A_1, A_2$ 交界处分居两个子区域的点,现在考虑交界处的点。应当意识到,交界处不会太大,这是因为当其宽度超过 $2h$ 的时候(其中有 $h = min(h_1, h_2)$)。多出来的点必然不会是距离最小的点,因为平行线间垂线段最短。所以我们就将分界曲的范围现在在了宽度为 $2h$ 即如图所示
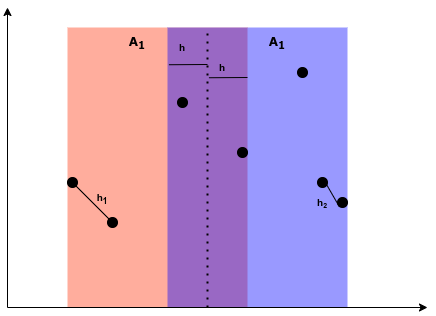
那么这样的分界区需要考虑的点是多少,由主定理可知 $T(n) = 2T(\frac{n}{2}) + f(n)$ 。如果 $f(n)$ 为 $\Omega(n^2)$,那么优化就失败了。而第一反应其实就是 $\Omega(n^2)$。因为我们要枚举分界区的点,分界区的点的个数是 $O(n)$ 。两两枚举就会导致 $\Omega(n^2)$。
但是我们证明这种情况不会发生,如图所示:
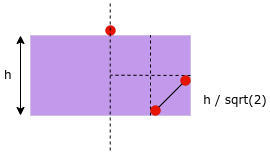
我们知道对于中上方的点,需要考虑的点就在下方的紫色区域(我们每次只考虑下方的点),会发现两个点不能在一个小格子里,这是因为如果真的存在,那么这两个点的距离小于 $\frac{h}{\sqrt2}$ ,显然也小于 $h$ 。然后就会发现了错误,这是因为图中的点属于 $A_2$ 区,所以他们的距离一定大于等于 $h$ 。也就是说,每个格子最多一个点,所以八个格子,最多 $8 - 1 = 7$ 个点(要去掉这个点)。
所以此时合并的复杂度就变成了 $O(n)$ 级别,所以根据主定理就可以快乐得出 $O(n\log n)$。