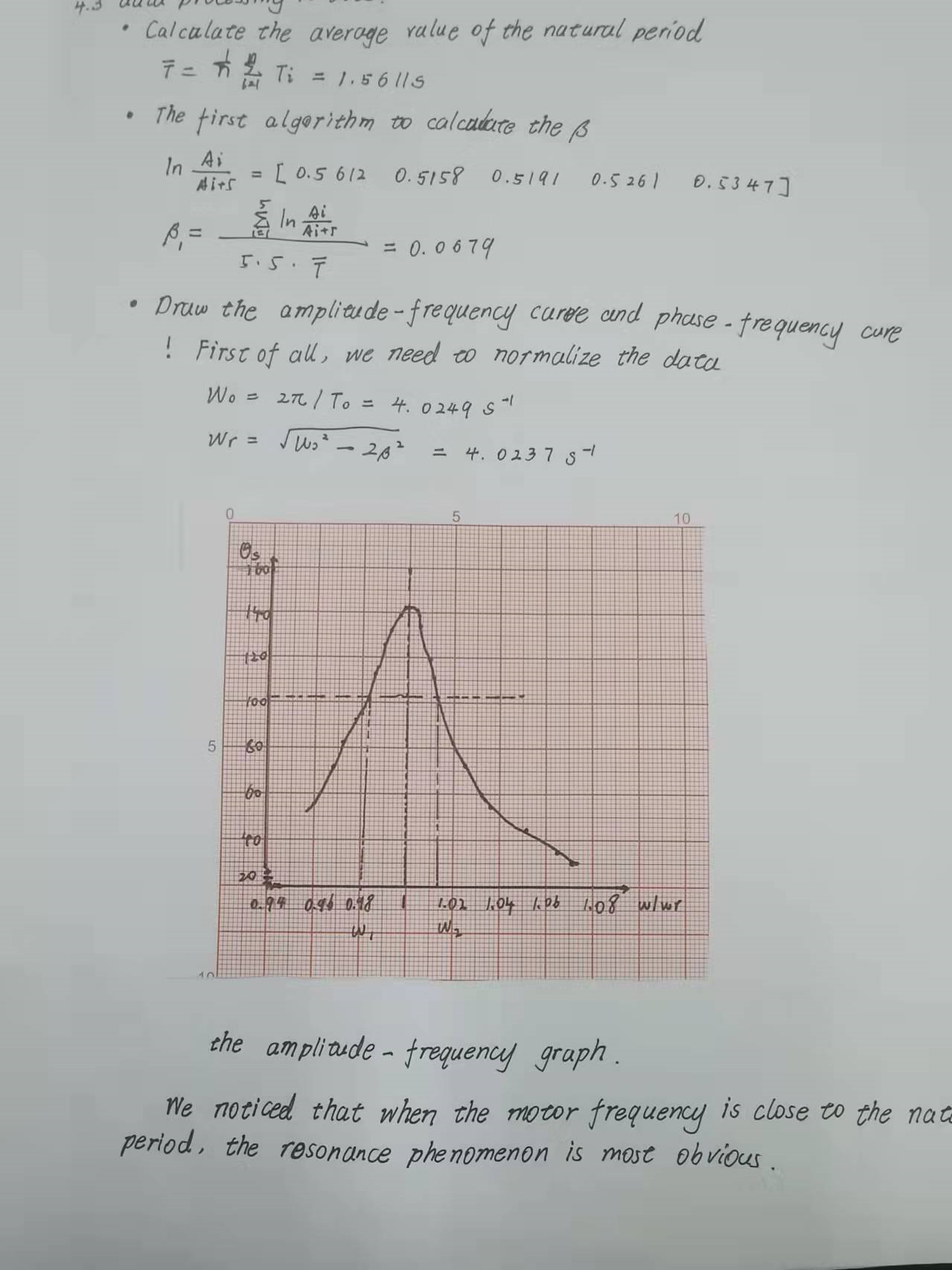
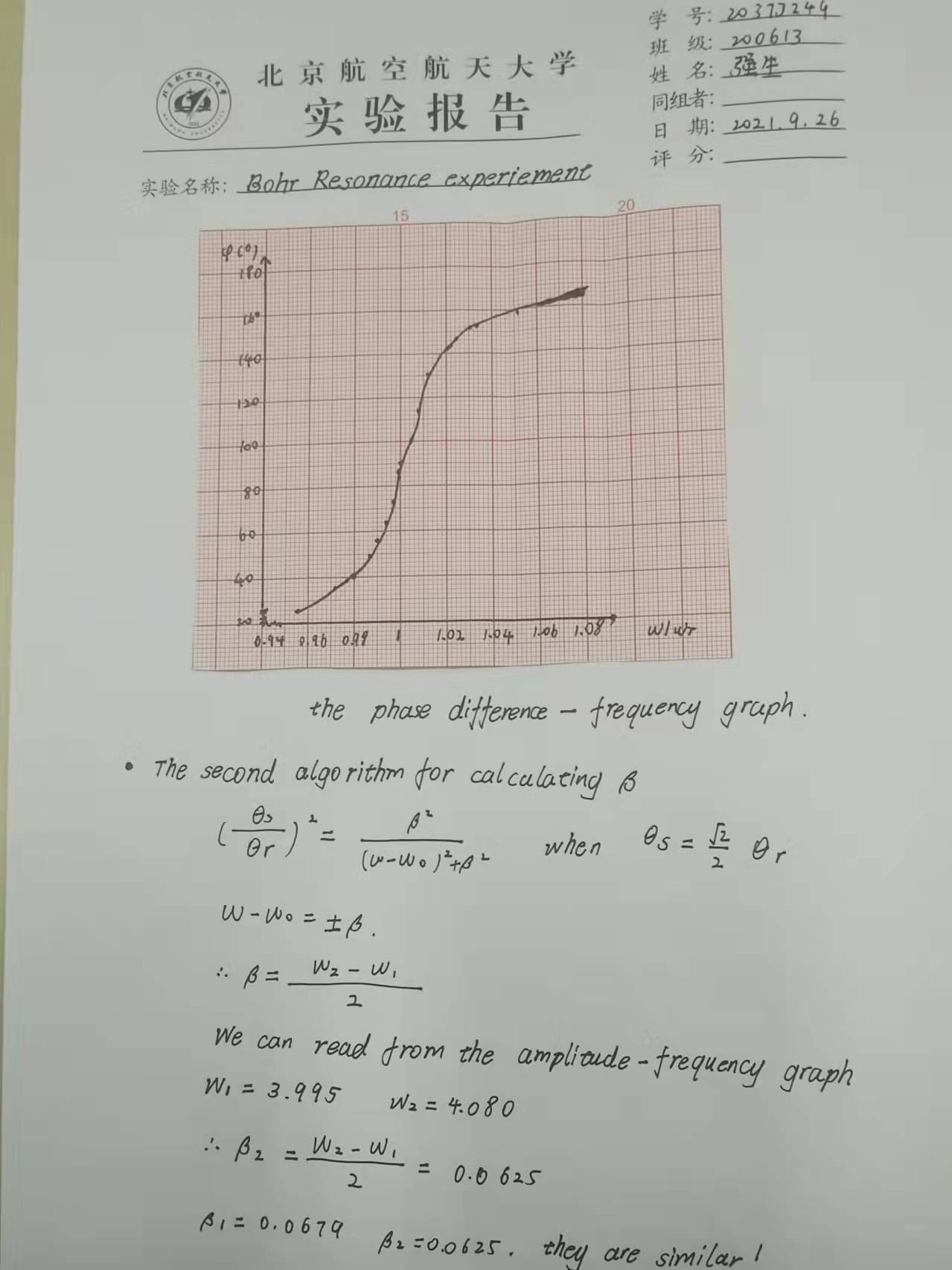
波尔共振实验作为2021年的新增实验,是我做过的所有实验中最简单的。
造成其简单的原因是这个实验全是交由仪器处理的,不存在因为操作失误而造成实验失败的情况。
波尔共振实验
一、总论
第一次选实验就选到了英文实验,还是一个新实验,就十分崩溃,所以确实投入了不少心血在这里面。总的来说这个实验室比我认识的人做的实验好像简单一些。我会在下面列举准备的措施,只要按照顺序阅读并践行,我认为开开心心通过不成困难。我现在能写这篇博客,离不开很多好朋友的帮助,特意在这里对对他们表示感谢。
鸣谢名单(按姓名字典序)
- 郭哥哥
- 梦拓小姐姐
- 向哥哥
二、实验组成
这个实验虽然看上去是一个,但其实由三个小实验组成,分别是自由振动、电磁阻尼振动和受迫振动,三个实验还是十分独立的,但是也是需要按顺序进行的,因为自由振动实验会得出固有频率,阻尼振动会计算出 $\beta $ ,这两个值都是要在第三个实验用到的。
三、实验的数学原理
这是本实验的最重要的一个式子,不要看这个式子结构这么复杂,其实只是因为涉及了转动而不是平动的原因,这其实就是转动版的牛顿第二定律,把右侧的每一项都弄懂就很容易明白这个式子的意义了。
我们可以看出这个这个式子是二阶微分方程的形式,所以可以知道,他的解一定是一个指数形式,所以为了让它更加和蔼可亲,我们用对两侧求对数的方法将其变为线性,进而就可以对其进行逐差法处理。
求对数就可以得到
虽然严格的说,还有一项带着 t ,但是已经可以看出是存在近似线性关系的。这样就可以用逐差法来处理了,其中的因变量就是 $ln\theta$ ,而自变量就是 t。
所以这个式子就显得很显然了。(上面的线性处理,都是在阻尼振荡实验中用的)
另外,在受迫振动的实验中,提供的参考资料里面用了归一化处理,如果不对频率进行归一化处理,也是可以完成实验的。对于没有受过相应的数学训练的人,第一次看到归一化处理的时候,会觉得莫名其妙,进而放弃(我就是)。
这里讲一下归一化处理,以考试举例,比如由A考试满分1000分,小明得了600分,B考试满分10分,小明考了9分,我们不能因为9 < 600, 就说小明更擅长A科,我们应该对两个考试采用统一的评判标准,比如得分率,小明A是0.6,B是0.9,所以小明B学科学的更好。我们可以看到归一化就是一个做比的过程。那么什么东西可用来做分母呢?总分可以,最高分也可以,平均分也可以。在这个实验中,我们为了说明在接近固有频率的时候(严格的说不是固有频率,因为会受到电磁阻尼的影响),受迫振动的振幅达到最大,所以我们用接近固有频率的那个值 $\omegar$ 来做分母,所有的频率都需要与它做比。在拓展实验中也有类似操作,做分母的是最大振幅 $\theta r$。
四、实验操作
基础的实验操作其实不需要看发的教材,因为不太直观,这里给大家安利一个B站视频,堪称保姆级教程,网址如下:
https://www.bilibili.com/video/BV1tB4y1F7Hp?p=4
此外,对于闪光灯,不要闲的没事拿起来,就让它放在那里就好了,不要像我一样,像拿个手机拍照一样,影响读数。
五、英文授课
作为一个英语废物,感觉英语授课友好程度还挺高的。我的老师是lb,他就是轮流问问题,答得上来就答,答不上来就过,当然我依然翻车了。这里给大家准备了一些资料。
常用词汇:
- Bohr resonance experiment 波尔共振实验
- amplitude 振幅
- frequency 频率
- phase-difference 相位差
- vibration 振动
- free vibration 自由振动
- damped vibration 阻尼振动
- oscillation 振荡器
- eletromagnetic 电磁的
- wheel 转轮
- period 周期
- equation 等式
- natural frequency 固有频率
- exponent 指数
- motor 电机
老师问过的问题:
- 第一/二/三个实验是什么?
- 第一/二/三个实验都需要记录哪些变量?都是怎样测量的?
- 第一/二/三个实验的关键点是啥?
- 你对第一/二/三个实验结果有何预期?
- 第一个实验你要怎样让转轮动起来?
- 在第一个实验中,周期与振幅有什么关系?
- 第一个实验为啥转轮会慢慢停下来?(我的翻车回答,到最后只能用中文说能量转换过程中会变成内能丧失,然后我就又被问了一波电磁阻尼的物理学原理,还有微分方程求解,幸亏考前看了一波)
- 第二个实验为啥比第一个实验更快停下来?
- 第二个实验的阻尼是哪种类型,为啥可以阻碍运动?
- 第三个实验怎么样测相位差?
- 第三个实验,你打算做几组数据,怎样选取数据点?
- 怎样改变电机的频率?
六、数据处理
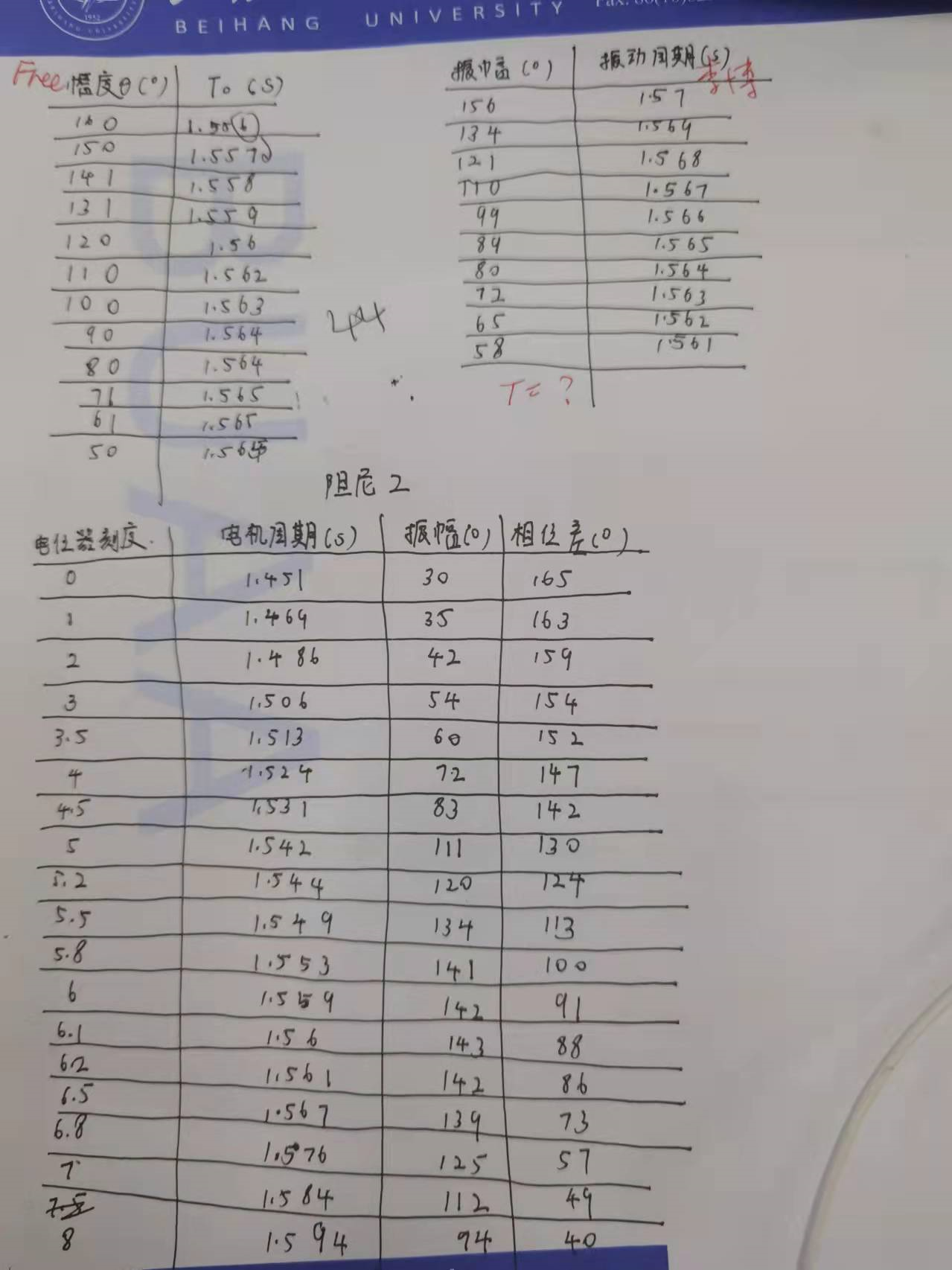
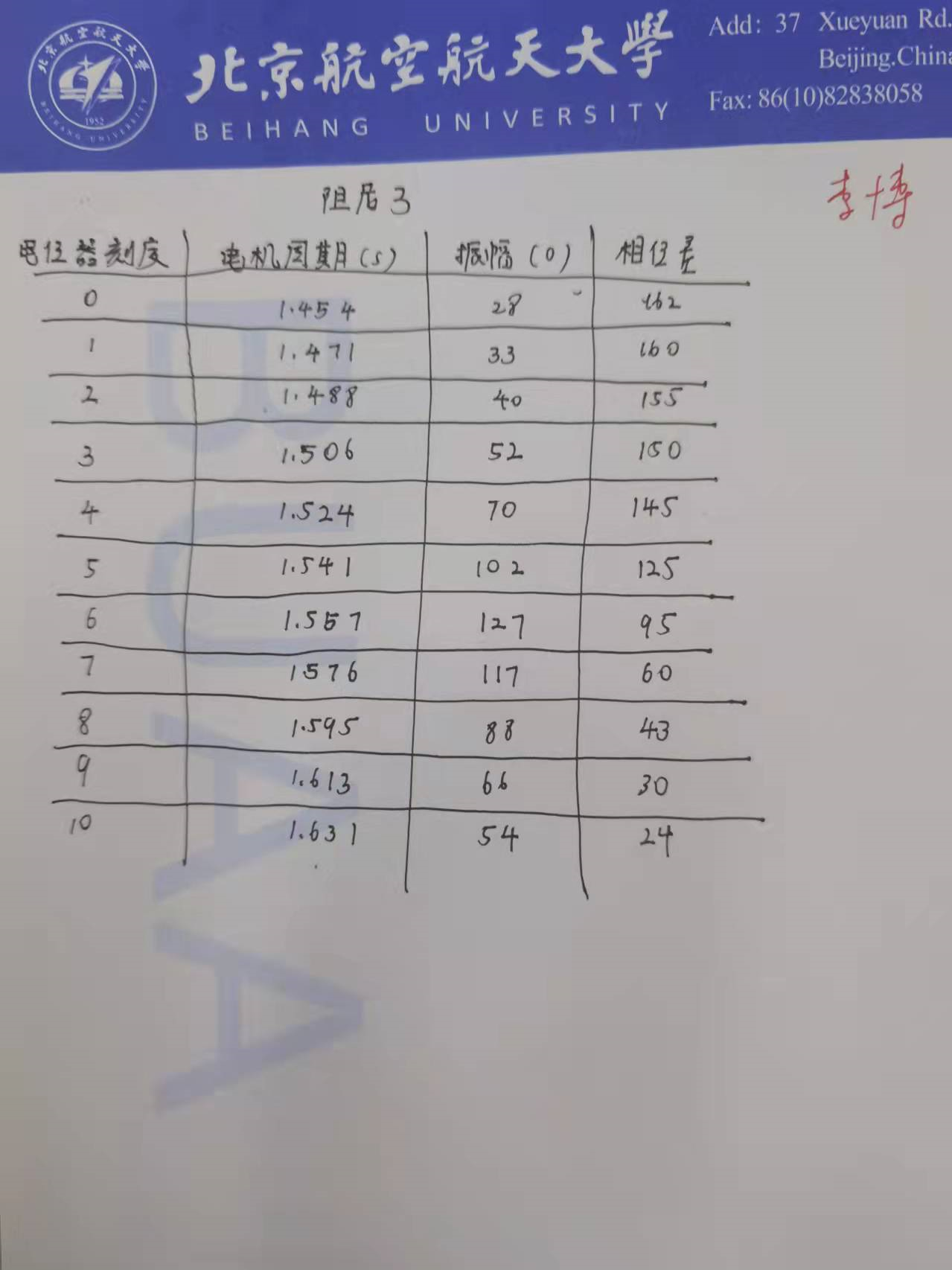
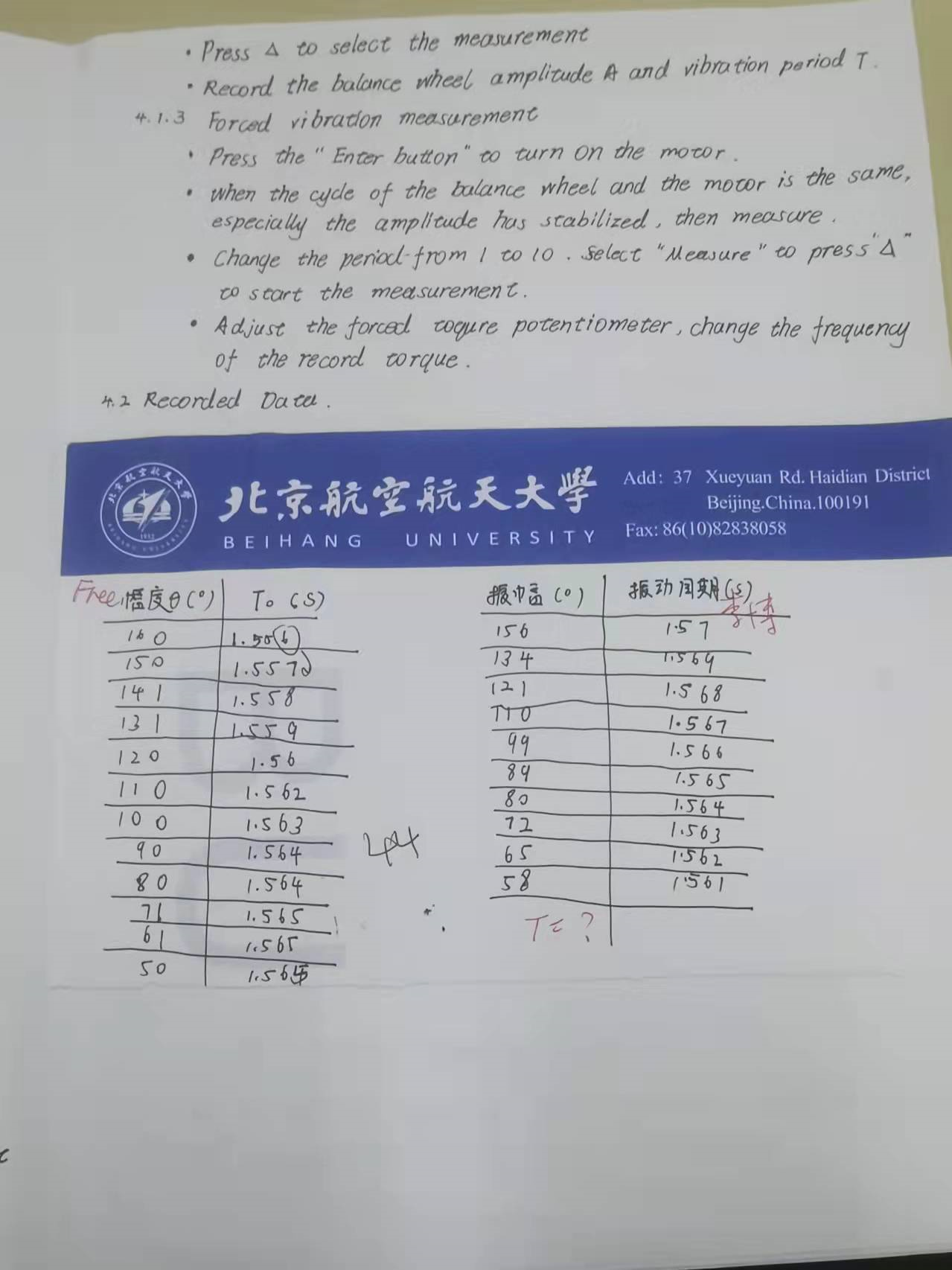
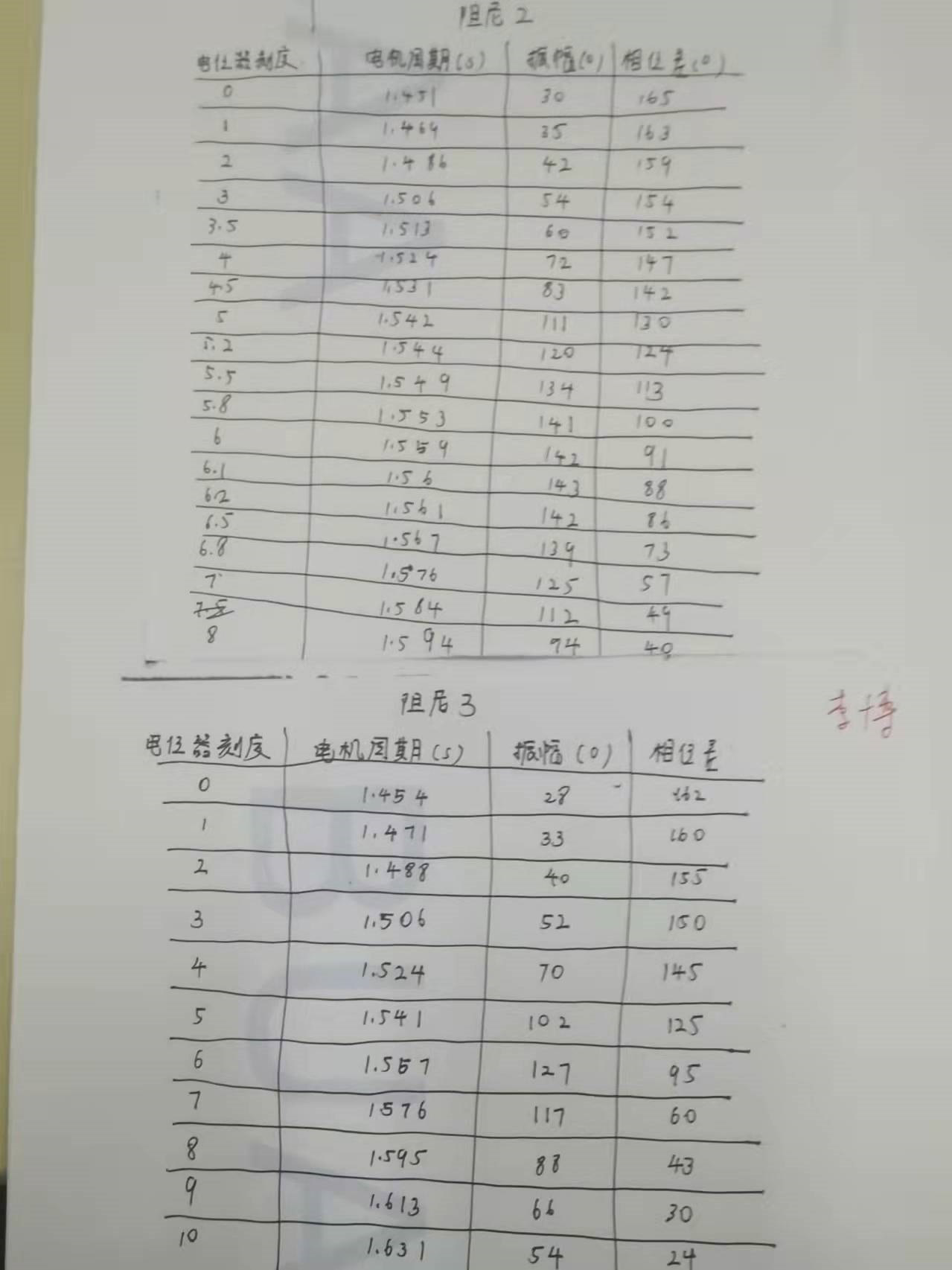
这个大家都说要当堂处理,但是好像只要把数据记在纸上,让老师签字就可以走了,但是我不确定是不是这样的,因为我当时太害怕处理数据翻车,就写了一个matlab脚本,来帮我处理数据,老师也看过我的程序了,所以可能是我这样也叫过了?
以下是源代码分享
%计算固有周期的平均值
T0 = xlsread('1.xlsx', 'B2: B13');%读取所有的自由振动T值
T0_bar = mean(T0)%对读取的T值求平均
%计算beta的第一种算法
theta = xlsread('2.xlsx', 'A2: A11');%读取所有的振幅
for i = 1:5
ln_theta(i) = log(theta(i) / theta(i + 5));%进行取对数处理以后用逐差法
end
T1 = xlsread('2.xlsx', 'B2: B11');%读取所有电磁阻尼振动T值
T1_bar = mean(T1);%对T求平均
beta1 = sum(ln_theta)/25/T1_bar%第一种求beta的算法,逐差法
%绘制幅频曲线和相频曲线
w0 = 2 * pi / T0_bar;%求出固有频率
wr = sqrt(w0^2 - 2 * beta1^2);%求出极值点
T2 = xlsread('3.xlsx', 'B2 : B24');%读取出受迫振动的周期
w = 2 * pi ./ T2;%计算出受迫振动的周期
rate1 = w ./ wr;%用极值点进行对频率进行归一化处理
thetas = xlsread('3.xlsx', 'C2: C24');%读取所有受迫振动的振幅
phi = xlsread('3.xlsx', 'D2: D24');%读取所有受迫振动的相位差
plot(rate1, thetas), figure, plot(rate1, phi);%绘制幅频和相频图
%计算beta的第二种算法
thetar = max(thetas);%取出最大振幅
rate2 = thetas ./ thetar;%利用最大振幅进行归一化处理
sp = csapi(w, rate2);%三次样条插值拟合
fnplt(sp), hold on, plot([min(w), max(w)], [1/sqrt(2), 1/sqrt(2)]), set(gca, 'XMinorGrid','on'), grid on;%绘制图像
w2 = 4.08, w1 = 3.955;%曲线与直线的两个焦点对应的两个频率即为所求
beta2 = (w2 - w1) / 2%第二种方法求beta
%计算beta1的不确定度
beta_group = ln_theta ./ (5 * T1_bar);
mean(beta_group)
std1 = std(ln_theta)/(5 * T1_bar)%可以中间接法测量theta的不确定度
std2 = std(beta_group)%也可以直接测beta,两者无明显差异
%误差分析改进
%选做实验,不同beta
这段程序可以实现注释中提到的功能,效果大概就是这样的:
为了保证脚本的正常运行,需要把脚本所在的文件夹如下配置:
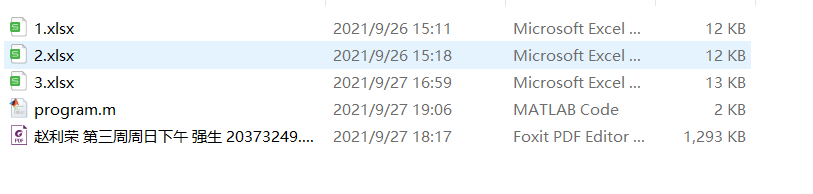
同时还需要对每个表格里内容具有如下限制(我的那个变量登记在哪列了,大家做实验的时候也要登记到相同的那一列,数据组数也不能多或者少),当然也可以修改我的脚本,很好改的:
截图里面的数据就是我做实验的数据,大家可以自己用来试试。
注释里不仅有功能说明,还有数据处理的方法,即使不用电脑处理数据,我觉得注释也是有一定的参考价值的。
考虑到有人不会matlab,其实用excel也可以做数据处理,就不在这里写VBA程序了(因为我不会,一步步截图太麻烦了)。
七、拓展实验
这个实验有两个拓展实验,一个是 $\beta$ 的第二种测量方法,我已经写在脚本里了,其中交点对应的频率 $\omega_1, \omega_2$ 需要从图中读出。是很简单的。
另一个是多个 $\beta$ 值的幅频和相频曲线,这个也很好做,只要有时间就可以做,脚本用用一个就可以了,但是一定要注意要做第二次第二个实验,不要以为只需要做第二次第三个实验,因为绘制图像需要第二问求出的 $\beta$ 的值,我就只做了第三个实验两次,就没法完成这个拓展实验了。
八、实验报告
就不放了,写的太烂太丢人。我只能说,对于英语废物,谷歌翻译YYDS!(快考试了,还是放出来吧)