并行计算-hw3

一、个人信息

条目	内容
学号	xxxxx
姓名	Thyrsael
学院	计算机学院
JobID	7995268

---

二、实验过程

首先用矩阵生成程序生成 $matrixA[1200 : 1600]$ 和 $matrixB[1600:2000]$ 两个矩阵

./matrixgen 1200 1600 matrixA
./matrixgen 1600 2000 matrixB

然后用串行程序进行计算求得时间，需要注意的是开启了 O2 编译优化以减小常数使结果更为客观

gcc -o tserial -O2 ./Tserial.cxx
./tserial matrixA matrixB matrixSC

输出为

Serial algrithm: multiply a 1200x1600 with a 1600x2000, use 16.8556230068(s)

然后采用并行程序进行计算，依然需要开启 O2 优化，最后结果为

--- 1600 x 1200 x 2000 matrix   number procs: 32        time: 1.6867085472(s) ---

实验截图如下

验证两个计算结果的一致性

cmp matrixPC matrixSC

发现结果一致，检验了程序的正确性。

最后计算加速比

$$\tt{acc\_rate = 16.8556230068 \div 1.6867085472 = 9.997}$$

可以看到加速了近 10 倍，足以见到并行计算的威力。

---

三、流程分析

3.1 泳道图

采用的是广播模式，所以与提供的源码（为点对点通信）显示的流程差异较大，我会在下面介绍具体的算法。

3.2 源码错误分析

死锁问题

在这里，没有考虑到当 numprocs > M 的情况，这会导致主进程没有给 id >= M 的进程发送任何信息 这些进程会一直处于等待中，造成死锁。

---1600x1200x2000 matrix       number procs: 32        time: 2.5864(s)---

如果采用原有代码的架构，可以考虑给 id >= M 的进程发送一条“约定信息”，当这些进程收到“约定信息”的时候，就会自动退出，不会造成死锁。大致如下

// 主进程
for (i = 1; i <= numprocs - 1; i++)
{
    if (i - 1 < M)
    {
        MPI_Send(A + (i - 1) * N, N, MPI_DOUBLE, i, 99, MPI_COMM_WORLD);
    }
    // 发送一条“约定信息”
    else
    {
        int dev_null;
        MPI_Send(&dev_null, 0, MPI_INT, i, 0, MPI_COMM_WORLD);
    }
}

// 从进程，收到“约定信息”后退出
if (status.MPI_TAG == 0)
                break;

再分配问题

这里再次发送的 $A$ 的行，不再是 i - 1 ，而应该是 numsend。只有这样才可以将剩余的行逐行分发。可以考虑如下修改

MPI_Send(A + numsend * N, N, MPI_DOUBLE, sender, 99, MPI_COMM_WORLD);

释放资源问题

从进程没有释放这两个分配空间（补上即可）

free(A_row);
free(C_row);

3.3 源码性能分析

点对点通信

点对点的通信代价过大，如果用广播形式会优化传播的效率，因为节点的通信形式可以变成网状或者树状。

定长数组

因为此题改成了从文件中读出矩阵，在读出之前，$A, B$ 的维度信息是不知道的。如果想使用定长数组，就必须要将其两个维度都赋一个极大的值，这就导致了在通信的时候传输的数据过大（每次都要传输一个大于实际矩阵的数组），造成了性能的低下。

可以考虑用 malloc 和宏来动态分配和访存，如下所示

/**
 * 宏定义，取矩阵中的某个元素
 * 申请空间 malloc
 * 只能得到一维数组，需要用下标计算得到数组中的每个元素，使用宏比较方便
 */
#define _A(i, j) (*(A + i * N + j))
#define _B(i, j) (*(B + i * P + j))
#define _C(i, j) (*(C + i * P + j))
#define _LOCAL_A(i, j) (*(localA + i * N + j))
#define _LOCAL_C(i, j) (*(localC + i * P + j))

// 分配空间
double *matrix = (double *)malloc((*pm) * (*pn) * sizeof(double));

在使用的时候，可以这样使用

// C[i][j] += A[i][k] * B[k][j];
_C(i, j) += _A(i, k) * _B(k, j);

通信流程

该程序的流程是多次分发的，首先给每个进程都分发一行，这是一个顺序过程，而不是一个并行的，这是第一个性能损失，如下所示

// 串行发送
for (i = 1; i <= numprocs - 1; i++)
{
    if (i - 1 < M)
    {
        MPI_Send(A + (i - 1) * N, N, MPI_DOUBLE, i, 99, MPI_COMM_WORLD);
    }
    else
    {
        int dev_null;
        MPI_Send(&dev_null, 0, MPI_INT, i, 0, MPI_COMM_WORLD);
    }
}

而且这次分发并没有结束，这就导致了再次需要通信的需求，这是第二个性能损失。

而且第二次分发必须要等到第一次分发顺序结束之后才可以继续分发，这就导致了分发的串行化，可能第 5 个进程早就完成了第一次的任务，但是必须等到前 4 个进程都领到第二次的任务，才可以领到第二次的任务。这导致了第三个性能损失。如下所示：

// 第二次分发，造成了损失
for (i = 1; i <= M; i++)
{
    sender = (i - 1) % (numprocs - 1) + 1;
    // 阻塞式接受信息，导致了串行，降低了效率
    MPI_Recv(C + (i - 1) * P, P, MPI_DOUBLE, sender, 100, MPI_COMM_WORLD, &status);
    if (numsend < M)
    {
        MPI_Send(A + numsend * N, N, MPI_DOUBLE, sender, 99, MPI_COMM_WORLD);
        printf("numsend: %d\n", numsend);
        numsend++;
    }
    else
    {
        // 发送标志为 0 的信息，让进程停止执行
        MPI_Send(&j, 0, MPI_INT, sender, 0, MPI_COMM_WORLD);
    }
}

正是因为有了上面的诸多问题，才有了新的模式的开发。

3.4 Scatter-Gather 模式

3.4.1 原理介绍

MPI_Scatter 和 MPI_Gather 都是 MPI 广播函数，其签名如下

MPI_Scatter(
    void* send_data,//存储在0号进程的数据，array
    int send_count,//具体需要给每个进程发送的数据的个数
    //如果send_count为1，那么每个进程接收1个数据；如果为2，那么每个进程接收2个数据
    MPI_Datatype send_datatype,//发送数据的类型
    void* recv_data,//接收缓存，缓存 recv_count个数据
    int recv_count,
    MPI_Datatype recv_datatype,
    int root,//root进程的编号
    MPI_Comm communicator)

MPI_Gather(
    void* send_data,
    int send_count,
    MPI_Datatype send_datatype,
    void* recv_data,
    int recv_count,//注意该参数表示的是从单个进程接收的数据个数，不是总数
    MPI_Datatype recv_datatype,
    int root,
    MPI_Comm communicator)

其实例图如下

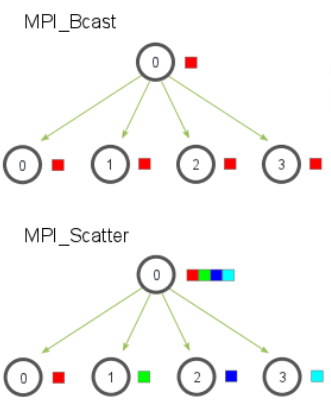
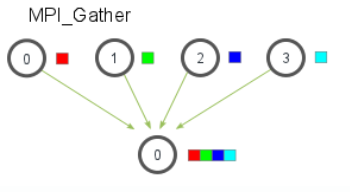
在并行矩阵乘法中，我们利用 MPI_Scatter 进行对矩阵 $A$ 进行块状（block）划分，如图所示：

对于大部分的矩阵 $A$ ，都可以均匀的分配给每个进程，对于无法均分的部分，最后将有主进程处理。还有一种思路是对于 $A$ 进行行补零操作，使其变成一个可以均匀分配的矩阵。但是依然需要主进程操作。

3.4.2 问题解决

死锁错误

当 numprocs > M 的时候，原有程序会死锁，但是在新的程序中，这只会导致主进程自己进行计算，分发的矩阵大小为 0，每个进程都会收到大小为 0 的局部矩阵，所以不会死锁。，如下所示

// 利用的是向下取整，那么有可能 localM * numprocs < M，也就是 A 矩阵没有被分配完
localM = M / numprocs;	// 当 numprocs > M 的时候这里会取 0
// 这里分发的大小也为 0
MPI_Scatter(A, localM * N, MPI_DOUBLE, localA, localM * N, MPI_DOUBLE, 0, MPI_COMM_WORLD);

再分配错误

只需要一次分配，所以自然没有再分配错误。

点对点通信优化

抛弃了点对点通信，采用了广播通信的形式，这就使得信息的传递路径更短，复用率更高。

通信流程优化

完全消除了之前源码中的形式，可以简洁优雅的进行单次通信，进程间的串行减少。

---

四、结果分析

4.1 线程问题

我们利用混合编程，利用了线程，所以最好将节点的数目调大，这样每个进程分布在不同的节点上，每个进程都可以利用其节点上的多个处理器核，达到加速的目的。

4.2 广播模式优化

借来小组同学的用 Send-Recv 程序进行测试，发现相同条件下（32 node，32 core，[1200 x 1600] x [1600 x 2000]），其时间为

time: 2.1495252177(s)

所以 Scatter-Gather 模式相对于 Send-Recv 程序的加速比为

$$\tt{acc\_rate = 2.1495252177\div 1.6867085472 = 1.27}$$

可以看到还是有一定优化效果的。

五、程序源码

#include <mpi.h>
#include <pthread.h>
#include <stdio.h>
#include <stdlib.h>
#include <sys/stat.h>
#include <sys/sysinfo.h>

// 程序计算 A[M x N] x B[N x P] = C[M x P]
double *A, *B, *C, *localA, *localC;
int M, N, P, localM;
int myid, numprocs;

/**
 * 宏定义，取矩阵中的某个元素
 * 申请空间 malloc
 * 只能得到一维数组，需要用下标计算得到数组中的每个元素，使用宏比较方便
 */
#define _A(i, j) (*(A + i * N + j))
#define _B(i, j) (*(B + i * P + j))
#define _C(i, j) (*(C + i * P + j))
#define _LOCAL_A(i, j) (*(localA + i * N + j))
#define _LOCAL_C(i, j) (*(localC + i * P + j))

/**
 * 从进程在计算的时候用这个结构体给线程传递参数
 * 这里削减了原有例程的参数，充分利用了线程的共享全局变量的特性
 */
struct threadArg
{
    int tid;
    int numthreads;
};

/**
 * @brief 线程要执行的内容，一个线程用于计算矩阵 C 一行的第 id + k * thread_num
 * (k = 0,1,...) 个元素
 *
 * @param arg 是一个 threadArg 结构体
 * @return void*
 */
void *worker(void *arg)
{
    int i, j, k;
    struct threadArg *myarg = (struct threadArg *)arg;

    for (i = 0; i < localM; i++)
    {
        for (j = myarg->tid; j < P; j += myarg->numthreads)
        {
            // localC[i][j] = 0.0;
            _LOCAL_C(i, j) = 0.0;
            for (k = 0; k < N; k++)
            {
                // localC[i][j] += localA[i][k] * B[k][j];
                _LOCAL_C(i, j) += _LOCAL_A(i, k) * _B(k, j);
            }
            // printf("%f\n", _LOCAL_C(i, j));
        }
    }

    return NULL;
}

/**
 * @brief 用于计算剩余行，计算的结果直接保存在 C 中
 *
 * @param arg 是一个 threadArg 结构体
 * @return void* NULL
 */
void *worker2(void *arg)
{
    int i, j, k;
    struct threadArg *myarg = (struct threadArg *)arg;
    int mod = M % numprocs;
    for (i = M - mod; i < M; i++)
    {
        for (j = myarg->tid; j < P; j += myarg->numthreads)
        {
            // C[i][j] = 0.0;
            _C(i, j) = 0.0;
            for (k = 0; k < N; k++)
            {
                // C[i][j] += A[i][k] * B[k][j];
                _C(i, j) += _A(i, k) * _B(k, j);
            }
            // printf("%f\n", _LOCAL_C(i, j));
        }
    }

    return NULL;
}

/**
 * @brief 从规定格式文件中读取矩阵
 *
 * @param filename 文件名
 * @param pm 指向行数的指针
 * @param pn 指向列数的指针
 * @return double* 读取出的矩阵首指针
 */
double *read_matrix(char *filename, int *pm, int *pn)
{
    FILE *fp;
    if (!(fp = fopen(filename, "r")))
    {
        printf("Can't open file %s\n", filename);
        exit(1);
    }

    // 读取维数
    fread(pm, sizeof(int), 1, fp);
    fread(pn, sizeof(int), 1, fp);
    // 为矩阵分配空间
    double *matrix = (double *)malloc((*pm) * (*pn) * sizeof(double));
    // 读取矩阵
    fread(matrix, sizeof(double), (*pm) * (*pn), fp);
    fclose(fp);

    return matrix;
}

/**
 * @brief 打印数组，主要用于调试
 *
 * @param matrix 待打印数
 * @param m 行数
 * @param n 列数
 */
void print_array(double *matrix, int m, int n)
{
    int i, j;
    for (i = 0; i < m; i++)
    {
        for (j = 0; j < n; j++)
        {
            printf("%10.4f", *(matrix + i * n + j));
        }
        printf("\n");
    }
}

/**
 * @brief 向文件中写矩阵
 *
 * @param filename 文件名称
 * @param m 矩阵行数
 * @param n 举着列数
 * @param matrix 指向矩阵的指针
 */
void write_matrix(char filename[], int m, int n, double *matrix)
{
    // buffer 是缓冲区，先把矩阵存入缓冲区再写入文件
    int bufsize = 2 * sizeof(int) + m * n * sizeof(double);
    char *buffer = malloc(bufsize);
    int i;

    // 向缓冲区写入矩阵的大小
    ((int *)buffer)[0] = m;
    ((int *)buffer)[1] = n;

    // dptr : double pointer，是 double 类型的指针，从 (int *) buffer + 2
    // 之后开始存储矩阵的元素
    double *dptr = (double *)(((int *)buffer) + 2);
    for (i = 0; i < m * n; i++)
    {
        dptr[i] = (double)matrix[i];
    }
    FILE *file;

    /**
     * 打开文件，写入 buffer
     */
    if (!(file = fopen(filename, "w")))
    {
        printf("Can't open file %s\n", filename);
    }

    fwrite(buffer, sizeof(char), bufsize, file);
    fclose(file);

    free(buffer);
}

int main(int argc, char *argv[])
{
    int i, j;
    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &myid);
    MPI_Comm_size(MPI_COMM_WORLD, &numprocs);
    // 计时器
    double start_time, end_time;
    // 线程个数
    int numthreads;
    // struct MPI_Status status;

    // 对于主进程，读取矩阵
    if (!myid)
    {
        A = read_matrix(argv[1], &M, &N);
        // print_array(A, M, N);
        B = read_matrix(argv[2], &N, &P);
        // print_array(B, N, P);
        // 输出读出信息
        printf("calculate [%d x %d] x [%d x %d]...\n", M, N, N, P);
        // 为结果矩阵分配空间
        C = (double *)malloc(M * P * sizeof(double));
    }

    // 发送 M，N，P 到从进程
    MPI_Bcast(&M, 1, MPI_INT, 0, MPI_COMM_WORLD);
    MPI_Bcast(&N, 1, MPI_INT, 0, MPI_COMM_WORLD);
    MPI_Bcast(&P, 1, MPI_INT, 0, MPI_COMM_WORLD);

    // 计算局部 A 数组相关信息
    // 利用的是向下取整，那么有可能 localM * numprocs < M，也就是 A 矩阵没有被分配完
    localM = M / numprocs;
    // 分配局部 A 空间
    localA = (double *)malloc(localM * N * sizeof(double));
    // 分配局部 C 空间
    localC = (double *)malloc(localM * P * sizeof(double));
    // 为从进程的 B 分配空间
    if (myid)
    {
        B = (double *)malloc(N * P * sizeof(double));
    }
    // 主进程计时，且在这里计时十分合理，计算了通信时间
    else
    {
        start_time = MPI_Wtime();
    }

    // 广播 B 矩阵
    MPI_Bcast(B, N * P, MPI_DOUBLE, 0, MPI_COMM_WORLD);
    // 分发 A 矩阵
    // 可以看到 Scatter 的参数和 Bcast 的参数很像
    MPI_Scatter(A, localM * N, MPI_DOUBLE, localA, localM * N, MPI_DOUBLE, 0, MPI_COMM_WORLD);

    // 获得每个进程的线程数目，其实这个获得的是处理器上核的个数，我的电脑就是 12 核的
    // 从这个角度看，想要算得快，可能需要分散开，每个进程都分布在不同的处理器上，才可以获得较好的表现
    // 但是这样通信的代价就会提高
    numthreads = get_nprocs();
    // 分配一组线程 id
    pthread_t *tids = (pthread_t *)malloc(numthreads * sizeof(pthread_t));
    struct threadArg *targs = (struct threadArg *)malloc(numthreads * sizeof(struct threadArg));

    for (i = 0; i < numthreads; i++)
    {
        targs[i].tid = i;
        targs[i].numthreads = numthreads;
        pthread_create(&tids[i], NULL, worker, &targs[i]);
    }
    // 等待线程计算完成
    for (i = 0; i < numthreads; i++)
    {
        pthread_join(tids[i], NULL);
    }
    // 收集结果
    MPI_Gather(localC, localM * P, MPI_DOUBLE, C, localM * P, MPI_DOUBLE, 0, MPI_COMM_WORLD);

    // 对于主进程而言，还需要计算剩余行和释放独有的资源
    if (!myid)
    {
        for (i = 0; i < numthreads; i++)
        {
            // 此时处理的行数减少到剩余行
            pthread_create(&tids[i], NULL, worker2, &targs[i]);
        }
        // 等待线程计算完成
        for (i = 0; i < numthreads; i++)
        {
            pthread_join(tids[i], NULL);
        }

        // print_array(C, M, P);
        end_time = MPI_Wtime();
        // 写入结果文件
        write_matrix(argv[3], M, P, C);
        // 输出时间
        printf("--- %d x %d x %d matrix\tnumber procs: %d\ttime: %.10f(s) ---\n", N, M, P, numprocs, end_time - start_time);
        // 只有主进程独有这两个资源，故独有的释放
        free(A);
        free(C);
    }

    // 每个进程都有这些资源，都需要释放
    free(localA);
    free(B);
    free(localC);
    free(tids);
    free(targs);
    // 结束通信
    MPI_Finalize();
}