面向对象-表达式

[TOC]

一、总论

1.1 题目特点

虽然这三周哪次作业题目描述都很多，多到经常看不懂的地步。但是应该怎么概括呢？又是一件需要仔细思考的事情。

我们可以看一看我们的要求，给出一个表达式，然后去括号，最后比较的是表达式的长度。如果来看 19 年的题目，那么是给出一个比较简单表达式，然后求导。两年的侧重点不同，比如 19 年的题目，会有提取公因式的操作（因为当不需要去括号的时候，提取公因式会让表达式变得更短），而 20 年的题目，多了自定义函数，这样给表达式的处理增加了难度。

我不妄加猜测课程组的意图，不过选择这样的题目作为第一单元的内容，肯定是有设计在里面的。在后续的实践中会发现，这个题目呈现一下特征

1.1.1 重结构轻算法

从数据结构的角度谈，表达式本身就是与树结构和栈结构密切相关，当然也不排除现实所有问题都可以找到合适的数据结构。但是表达式明显的无穷无尽的递归特性，还有已经有了数据结构基础的前置引导。很难让人不选择树结构作为解题的关键（栈结构可以看做隐式地建立了一棵树，毕竟具有等价性）。而树结构又绑定了一大堆算法，比如说 DFS，BFS，这种遍历几乎是唯一的算法模型。可以说，只要独立的思考出要采用树结构，那么可以说，架构设计最关键的部分已经被解决了。不过课程组已经给了联系单元做明示，我个人解题的时候不是去思考要用一个树结构，而是自己想出了一个算法，然后发现原来是树上的算法，然后暗自震惊一下，继续 debug。

从算法的角度看，我将其分为两个部分，一个是与树相关的，一个是与树无关的。与树相关的算法可以说很精妙，难以理解，除非意识到这是一个与树相关的算法，才能把树的知识迁移过来辅助理解，比如说递归下降法，如果没有意识到这是一个建树的过程，或者说意识到这是一个 DFS 的话，那么甚至理解他是一个递归算法都困难，因为它并没有自己调用自己，而是几个函数在一起转着圈的调用。而与树无关的算法都极其简单，而且甚至缺少设计空间，比如加法，其实就是根的节点组对应的表达式里的每一项都写到一起，跟没说一样，再比如乘法，就是系数相乘，指数相加，没有一点优化空间，就好像没有办法去优化 1+1=2 一样。而性能优化采用的算法，大体思路也是极其丑陋的，比如合并同类项就是把相同的项相加，然后删掉；做三角的平方和优化，就是把原来的平方项去掉，乘上一个新的项，其他优化都是如此，都是以遍历和简单数组操作为主。哪怕不谈具体的优化，优化总体的设计感也并不好，我见到的，都是一项优化一项优化的作，然后不断的尝试，最后记录下来一个最好的结果。对于优化的调度，就是重复的试错，大量的试错的思路，比枚举还要朴素。可以说做优化的唯一难点就是“说服自己，采用这个丑陋的算法，而不是冥思苦想，不得结果。”

当然这么说有失偏颇，比如我看 19 级陈昊哥哥的博客，里面的计时熔断机制，而且对于替换调度的队列结构（这个我到现在都没有实现，应该是有特定的数据结构支持），可以说给人一种极端的暴力美感，是十分优秀的，十分体现算法智慧的。

1.1.2 重架构设计

我给架构的定义就是解决整个问题的总体设计。比如说我的架构设计就是“输入 -> 建立在 AST 递归解析 -> AST -> 标准项集合 -> 建立在标准项的优化 -> 输出”。我现在对于架构的追求就是尽量解偶联。解偶联的好处在于，工作就那么多，只要把任务分的更多，每个任务就可以分的更小更简单。

不可否认，得出“重架构设计”的结论应该有我个人的主观因素的影响，因为我的特点就是没有实力做出很漂亮的细节。比方说我身边很多人是没有标准项这层结构的，很多人可以采用树结构进行运算和字符串输出，无疑是需要更加强大的算法能力，而我是不具有。我只有把输出的任务从树结构上剥离出来，单独做出一个标准项集合来承担这个工作，才比较符合我的性格。

我在后面希望能够达到的目标是局部的算法水平不超过整体的架构设计水平，如果算法水平过高，那么就把这部分算法拿出来单独作为一个架构结构进行设计。像那些只用树可以输出字符串的项目，其实在算法实现的过程中，已经在中间实现了某些类似标准项的结构，只是没有单独做出来而已。我称为这种现象就是局部算法超过了整体的架构设计，是我不希望见到的。

之所以有这样的想法，是因为当一个算法的等级提高（从局部升级到整体），那么服务它的数据结构和算法就可以更加精细的操作，比如说这个部分就可以进行面向对象的设计，而不是在一个方法里面腾挪。而就我个人实践而言，确实有这种倾向。

当然并不是不允许强悍的算法设计，架构设计也不应该是靠算法的复杂倒逼的。架构设计最重要的就是贴切，贴切于解空间，贴切于到达解的路径。比如说在实现自定义函数的带入的时候，在树上直接操作的算法难度要高于预处理字符串，但是在树上操作，更加符合题目的思路，所以还是应当采用树上的实现。

前面似乎有埋汰预处理字符串的嫌疑，但是其实如果预处理字符串设计的足够巧妙，比如说蕴含了递归的思想，这何尝又不是一种对树结构压力的分担呢，又何尝不是一种优秀的设计呢？

1.2 架构设计

1.2.1 整体架构

整体架构分为如下部分

组成	结构	算法	功能
解析	树	递归下降	根据输入字符串建立树
抽象语法树	树	递归遍历	根据抽象语法树生成标准项集合
标准项集合	集合	增删改查	包括运算，优化，输出三大功能

架构图如下：

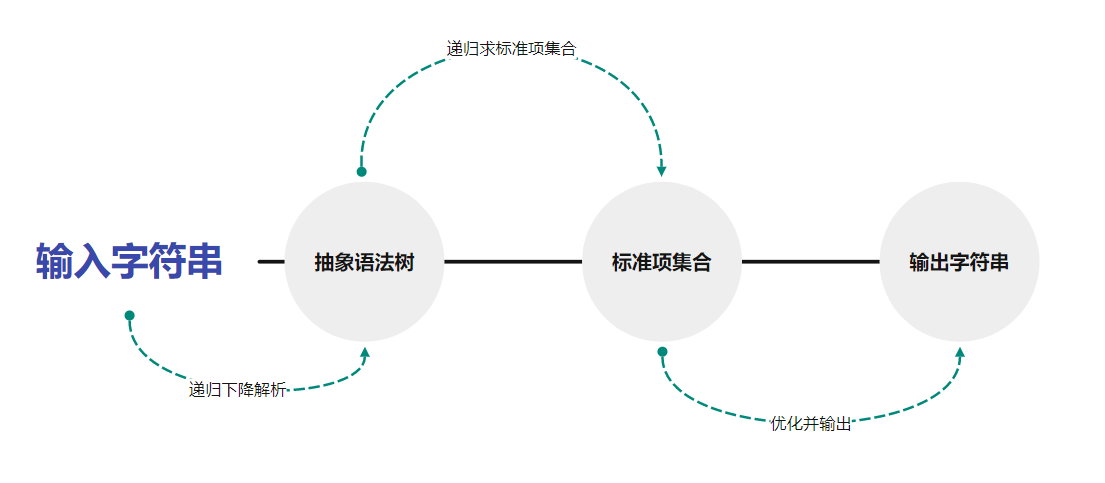
1.2.2 类设计

类设计如下：

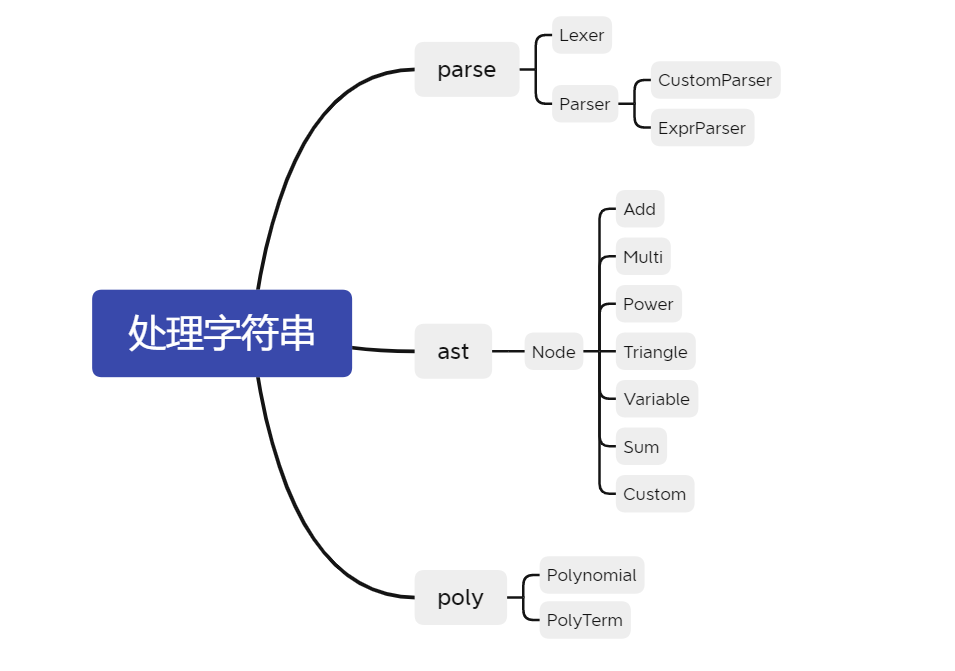
parse 包下有 Lexer，Parser，CustomParser，ExprParser。Lexer 是每个 Parser 必须有的属性。因为解析自定义函数的定义和解析表达式存在一定差异，所以现有 Parser 抽象类，CustomParser，ExprParser 继承了 Parser。

ast 包下所有类都实现了 Node 接口，这是为了 AST 的一致性问题。

poly 包下有 Polynomial，他管理着一个 PolyTerm 的集合。

1.3 设计思想

1.3.1 齐物观

都是画眼睛的高光，有人喜欢用橡皮，有人喜欢用电动橡皮，有人喜欢用小刀划，有人喜欢用 12B 去衬，有人喜欢用白颜料去点，有人喜欢直接将眼睛从画面中抹去，有人喜欢将高光画成黑色，有人用摘下雪花作为高光，洁白而且温暖，有人画的不好，却会讲故事。

我只是喜欢那双眼睛，其他皆可齐物。

1.3.2 代码分类

仅代表我个人观点，我感觉面向对象对我们的帮助不在于帮我们解决更难的问题，而是帮助我们解决规模更大的问题。

就我个人观点，面向对象由一部分是对代码进行分类。分类是一种人本位的思想，他默认我们可以对任何客观事物完成主观上的抽象与分类。这点上我持观望态度。

上图是竹子的花，因为古典植物学坚持以繁殖器官的解剖结构对植物进行分类，而竹子具有开花难，花期短，花的结构存在普遍差异性的特点，成为了分类学的难题。

---

二、标准项集合

2.1 倒着讲

虽然算法是“解析，建树，建集合，输出”这样一个过程，但是要是从理解的角度，我更愿意倒着讲述。这是因为标准项集合跟现实中的运算更为类似，后面的数据结构也会调用他的方法，所以不然先放到前面来讲。

2.2 格式

这里说的是标准项的格式，大概是这个样子的

$$a \times x^b \times \Pi \sin \times \Pi \cos$$

也就是说，想要确定一个标准项，就要确定他的系数、指数、三角函数列表，三角函数又有内容和幂次的属性。

这里首先要明确，这是一个数学概念，是可以用多种数据结构来实现，不同的数据结构是为了需求的不同而设计的，比方说我的标准项设计，就用到了 HashMap 的结构。但是其实最容易想到的是用 ArrayList 来存。我这么做是服务于乘法。

private BigInteger coefficient;
private BigInteger exponent;
private HashMap<Polynomial, BigInteger> sin;
private HashMap<Polynomial, BigInteger> cos;

标准项集合描述的就是一堆标准项，其形式如下

$$a_1 \times x^{b_1} \times \Pi^1 \sin \times \Pi^1 \cos + a_2 \times x^{b_2} \times \Pi^2 \sin \times \Pi^2 \cos + ...$$

我个人这里偷懒了，直接采用的是 ArrayList，

private ArrayList<PolyTerm> polyTerms;

但是如果细致考量，就会发现 ArrayList 赋予了每个标准项顺序的概念，而对于标准项来说，朴素的看，每一项应该是等价的，即满足加法交换律，所以无脑的用 ArrayList 不是一个很好的设计。

对此我想了两个比较好的优化结构，一个是 HashSet，它模糊了顺序的概念，这样比较两个项的时候，就可以不用管顺序了，也就是说，满足了加法交换律。对于 ArrayList 而言

$$x + x^2 \neq x^2 + x$$

但是 HashSet 没有这个问题。

此外就是对标准项实现 Comparable 接口，这样就可以利用 ArrayList 的排序功能，完成相同标准项集合的比对。

2.3 方法

我觉得这里的方法设计消耗脑力最少，而且可以设计出实现各种功能的方法。这些方法还可以进行组合，生成更加复杂的方法。给人的感觉就是在定义数学的运算空间一样。这里仅介绍与运算相关的方法：

方法	解释
add	描述两个多项式相加的结果
multi	描述两个多项式相乘的结果
isZero	判断当前表达式的值是不是 0
negative	描述一个多项式的负值

剩下的方法在优化部分介绍。

---

三、拙劣的抽象语法树

3.1 树结构

还是先明晰一点，就是形式化表述与树结构并不那么等价，在形式化表述里，对于树的强调并不多，甚至给人一种“Expression 是 Term 的集合，Term 是 Factor 的集合”的感觉，这种感觉很不利与我发现树。而且有的因子，并不对应一个叶节点，比如 x**2 其实他对应的是这样的一种结构

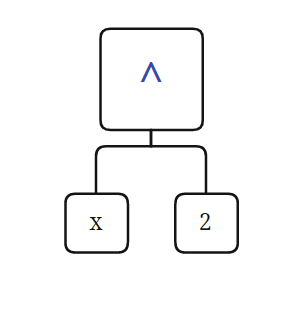
而不是一个节点，像这样

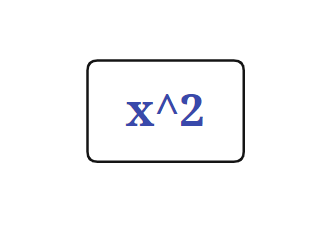
也就是说，这棵树，更像是数据结构里的表达式树，里面是没有 Expression，Term，Factor 概念的

其次，是这棵树的来源问题，这棵树是我从网上看了好多代码以后找出来我比较喜欢的一款，应该是叫做抽象语法树（Abstract syntax tree，AST）。但是我看人家都是解决那种特别复杂的问题的，而且我看见那个还是个二叉树，而我这个应该是多叉有序树，所以不确定是不是，就放这里，有兴趣再了解吧。

3.2 举例

还是举一个例子，来明确一下这棵树的样子，这是表达式

sin(x**3)**2*x-f(x,x**2,(x+1)**2)+(x**2+1)*sum(i,1,3,i**2)

转换成表达式树，就是如下结构

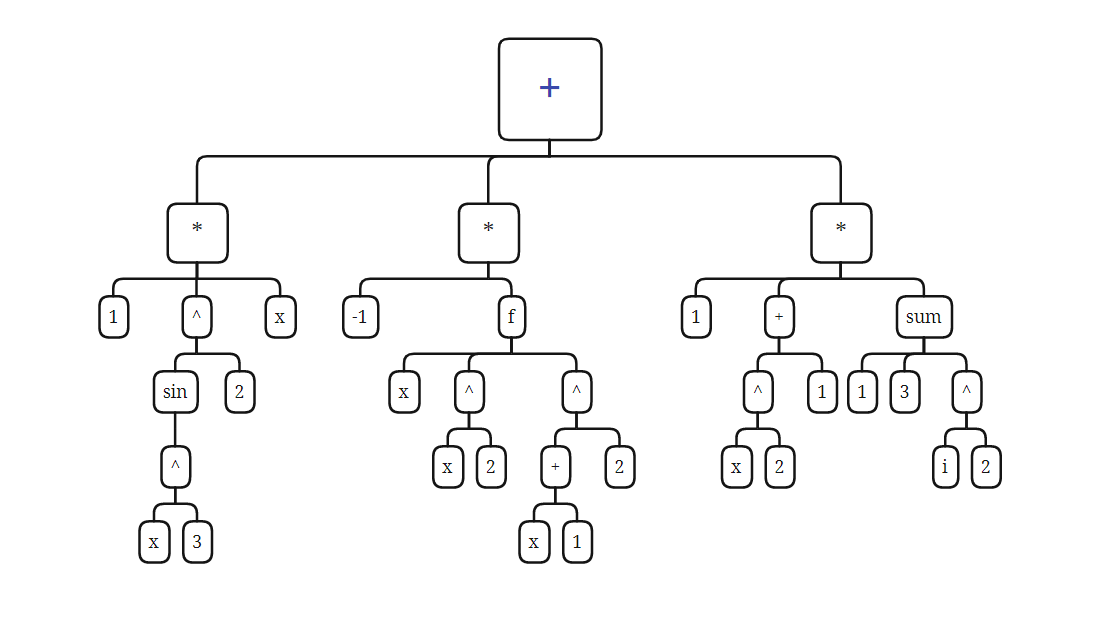
这里面，每一个方框就是一个节点，也就是一个类，这些类均实现了 Node 接口，方便管理。（除了幂次，我没有写成图那样，因为那样有点繁琐，标准项不适合幂次运算）。

3.3 Node

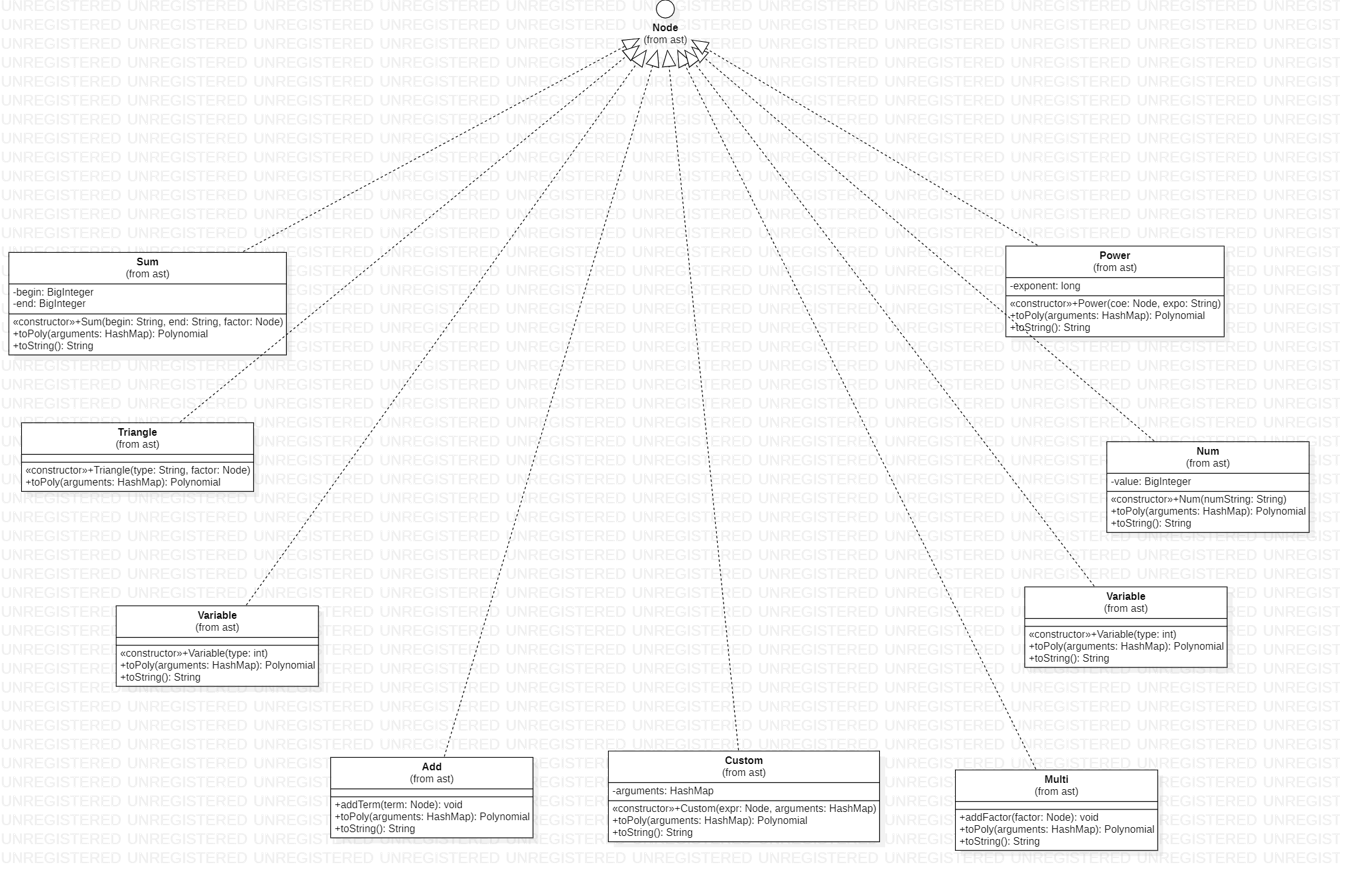
我们构建这棵树的目的就是为让它通过递归，生成我们的标准项集合，所以每个节点其实完成的是一件什么事情呢？是他的所有孩子都已经标准项集合化了，它需要把孩子们的标准项集合经过一定的处理，生成一个标准项集合，并返回给其父节点。那么要经过怎样的处理呢？这其实是由两部分组成，即

• 运算
• 运算法则

运算部分是在标准项集合中实现的，比如加法，乘法。而运算法则是节点的信息，比如说 Add 的运算法则就是对所有的孩子进行加法运算。这个是比较直观的，稍微复杂一点的是 Power ，他的法则是将底数（他的一个孩子节点）进行乘法运算指数次。代码如下

public Polynomial toPoly(HashMap<Integer, Node> arguments)
{
    ...

    for (long i = 0; i < exponent; i++)
    {
        polynomial = polynomial.multi(factor);
    }
    return polynomial;
}

3.4 自定义函数

自定义函数看着挺难的，但是其实很简单，只需要意识到，自定义函数也是一种运算节点，只不过它的运算法则更为复杂，是以一棵表达式树定义的（就是我们用 CustomPaser 解析出来的树，往下看就知道了）。我们践行这种运算法则的方式就是遍历这棵树，并且在合适的位置将形参换成实参即可。因为不让放代码，所以不能说的太清楚。

---

四、解析

4.1 形式化表述与递归下降法

我个人最大的一个体会，就是形式化表述与递归下降法是对应的，甚至在数学上是等价的。但是指导书里的形式化表述还不是最终形式，这里安利一篇博文（找不到了，大概就是这样，具体的忘了，肯定不严谨），他在最开始的时候将形式化表述做了一个转化，我觉得更有 DFS 的感觉了。

$$Expr -> Term \quad| \quad Term\quad Expr \\ Term -> Factor\quad| \quad Factor\quad Term\\ Factor -> factor1 \quad| \quad factor2 \quad | \quad factor3$$

4.2 递归调用

因为递归下降很难看出来，因为不是传统的递归，即自己调用自己，而是一种循环的调用。我们以第三次作业中 parse 的逻辑来谈，可知如图：

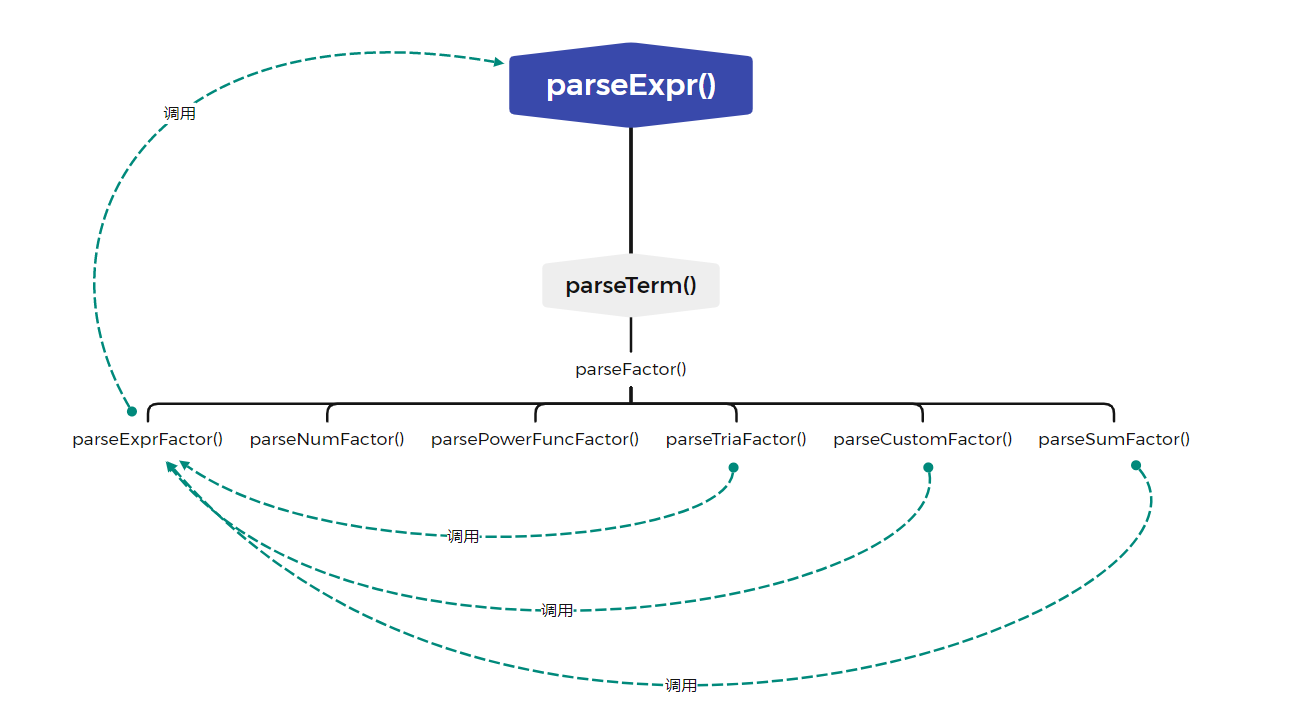
可以看出，所谓的递归调用，就是 parseExpr() -> parseTerm() -> parseFactor -> parseExpr 的一个过程。可以发现是一个循环。

4.3 掩盖细节

如果观察我的主代码就会发现，在解析部分其实只出现了一个 ExprParser 类，如下

public static void main(String[] args)
{
    ExprInput scanner = new ExprInput(ExprInputMode.NormalMode);
    int n = scanner.getCount();

    ExprParser parser = new ExprParser();

    for (int i = 0; i < n; i++)
    {
        parser.addFunction(scanner.readLine());
    }

    parser.setLexer(new Lexer(scanner.readLine()));

    Node tree = parser.parseExpression();

    Polynomial polynomial = tree.toPoly(new HashMap<>());

    System.out.println(polynomial.selectShortest());
}

可以看到，没有出现 Lexer,CustomParser 类，这是我觉得设计比较好的地方，用户程序员其实没必要掌握 Lexer,CustomParser 的知识，其实只要给他呈现一个解析器就好了，Lexer,CustomParser 出现在 ExprParser 的内部，我觉得是一个很好的封装处理。

4.4 类设计

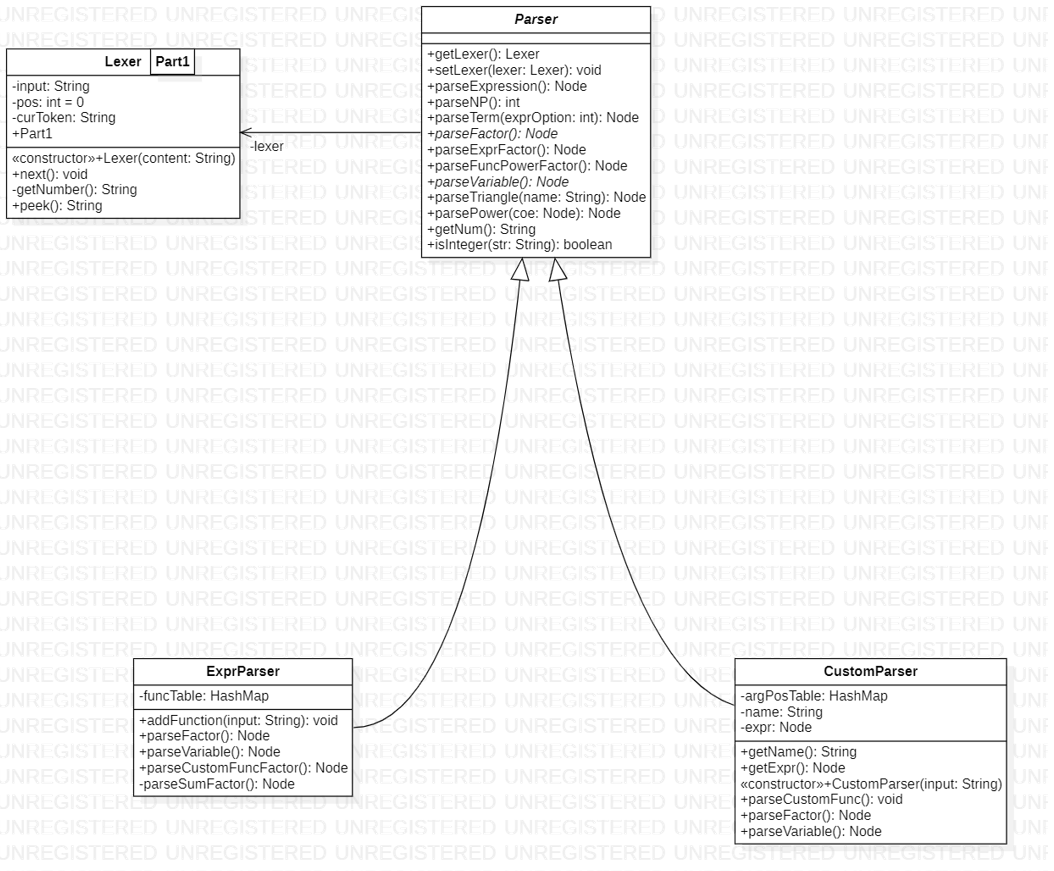
4.3.1 Lexer

译作词法分析器，其实好像没那么玄，就是把一个一个的字符拆成有意义的语义元素，比如将 sin(x**2)**3 就顺序拆成 sin，(，x，**，2，)，**，3 即可。

对于实现的方法

方法	功能
next	Lexer 移动指向下一个元素
peek	返回 Lexer 当前指向的元素

对了，我个人觉得如果把 Lexer 作为 Parse 的一个内部类，封装性会更好。

4.3.2 Parser

Parser 只有一个属性，就是 lexer，可以说如果不是 lexer，parser 的大部分方法其实写成静态更好。这里就涉及到一个关于面向对象的朴素思考，即一个类必须封装一些属性，然后再封装一些以这个属性为参数的函数，不然就没有面向对象的意义。

作为一个抽象类，其中其实实现了大部分方法，在这里展示一下递归下降的写法，对于 parseExpr，parseTerm，有

Term parseTerm()
{
	factors.add(parseFactor)
	while(有分隔符)
	{
		factors.add(parseFactor)
	}
	
	return term;
}

而对于 parseFactor，是交由子类实现的，但是大体的思路是一致的，都是根据当前语义元素进行判断，选择出具体的 factor 类型，然后调用具体的方法。

Factor parseFactor()
{
	if (语义元素是表达式)
	{
		factor = parseExpressionFactor();
	}
	else if (语义元素是数字)
	{
		factor = parseNumFactor();
	}
	else if (语义元素是幂函数)
	{
		factor = parsePowerFuncFactor();
	}
	else if (...)
	{
		....
	}
	
	return factor;
}

4.3.3 CustomParser

CustomParser 是一个专门解析自定义函数的定义的 Parser，相较于普通的 Parser，他多了三个属性，而这三个属性刚好代表他功能的特殊性。

属性	解释
HashMap<String, Integer> argPosTable	完成一个由形参名到形参位置的映射，比如说 f(y,z,x)，则有 y -> 1, z -> 2, x -> 3
String name	该自定义函数的名字，比如 f,g,h
Node expr	该自定义函数的表达式，是一种树结构

当我们用 CustomParser 解析一条定义的时候，他需要告诉我们，这个函数的名字是什么，这个函数的表达式是什么，而且这个表达式已经经过了处理，在变量部分已经变成了形参的位置，而不是形参名（这是因为形参 y 可以出现在第一个位置，也可以出现在第二、三个位置，所以没办法确立替换规则）。我们需要在 Variable 节点里包含的信息是“第一个形参，第二个形参……”，而不是“x，y……”。

4.3.4 ExprParser

这是用来解析待化简的表达式的类，可以说是在解析部分最重要的类。经过它的解析以后，我们会生成我们需要的树结构。

这个最大的容易出 bug 就是 lexer 的移动问题，真的超容易出 bug，放一个解析 sum 的给大家感受一下

private Node parseSumFactor()
{
    // 此时指向 sum
    getLexer().next();
    // 此时指向 (
    getLexer().next();
    // 此时指向 i
    getLexer().next();
    // 此时指向 ,
    getLexer().next();
    // 此时指向 begin
    final String begin = getNum();
    // 此时指向 ,
    getLexer().next();
    // 此时指向 end
    final String end = getNum();
    // 此时指向 ,
    getLexer().next();
    Node factor = parseFactor();
    // 此时指向 )
    getLexer().next();
    return new Sum(begin, end, factor);
}

然后这个方法就 bug 了，de 了好久。

---

五、优化

5.1 合并同类项

这里我做了两版，一般是普通的合并同类项，采用的方法就是判断两个标准项的幂次，三角是不是相同，写作下面

return exponent.equals(other.exponent) && sin.equals(other.sin) && cos.equals(other.cos);

第二版就更加灵活一些，考虑到这样的情形

$$\sin(x-1) = -\sin(1-x)$$

所以放宽了比较的条件，每次进行比较的时候，先比较一次 x-1 和 x-1 ，在比较一次 x-1 和 -x+1 。这样就可以达到合并更多的同类项的目的。这是用 negative 方法实现的。

需要注意的是，不是每次变换，都需要修改系数的值，sin 的奇数次才需要修改，cos 永远不需要修改

$$\sin(x-1) = -\sin(1-x)\\ \sin^2(x-1) = \sin^2(1-x)$$

5.2 去零

这里也是写了两版，第一版是直接判断系数为不为 0，如果为 0，那么就认为这个标准项为 0。这里刚学了 lambda 表达式，就献了个丑。（不是这节的重点）

polyTerms.removeIf(e -> e.getCoefficient().equals(BigInteger.ZERO));

lambda 表达式分为三个部分，即：

• 参数，一般用 () 括起
• 连接符，即 ->
• 函数体，可以是一个表达式或者一个语句块。如果是一个表达式，表达式的值会被作为返回值返回；如果是语句块，需要用return语句指定返回值。

第二版去零考虑到了这些情况

$$\sin(0),\sin((x-x))$$

所以是这样实现的：

public boolean isZero()
{
    // 系数为 0，则整个项为 0
    if (coefficient.equals(BigInteger.ZERO))
    {
        return true;
    }
    else
    {
        for (Polynomial p : sin.keySet())
        {
            // sin 的因子为 0，则整个项为 0
            if (p.isZero())
            {
                return true;
            }
        }

        return false;
    }
}

5.3 平方和

这个看上去挺难的，但是怎么说呢，其实只要硬着头皮写，是可以写出来的。我个人经验，如果在标准项层面实现不了，那么就把他转换成标准项集合看看能不能实现，效果十分好，这是因为标准项集合拥有的方法更多，更接近数学定义。算法流程如下：

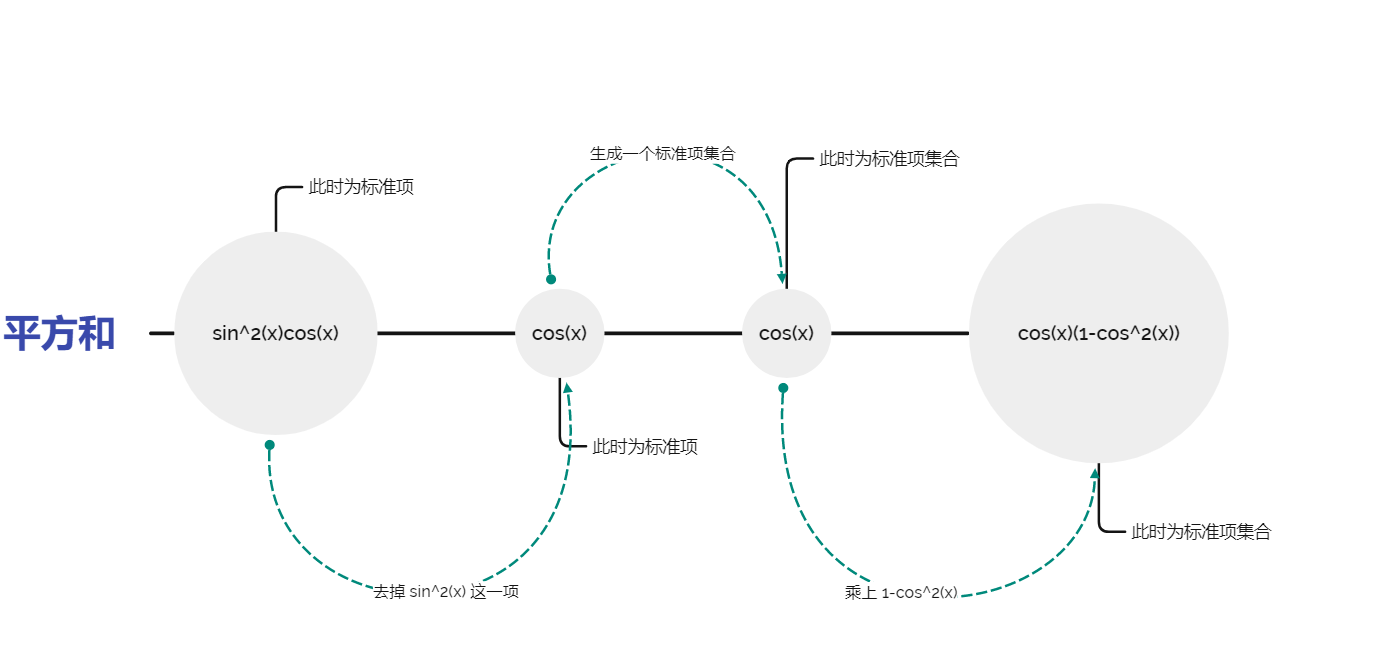
此外，还需要注意的是，从 Map 去掉某一项的操作容易抛出异常（第十个点 RE ），具体原因和解决办法这里有：

https://blog.csdn.net/weixin_40807247/article/details/88413347

5.4 诱导公式

不是特别复杂的诱导公式，就是很普通的

$$\sin(x) = -\sin(x)\\ \cos(x) = \cos(-x)$$

这个就更简单了，可以在标准项层面就完成，不需要升级到标准相机集合的层面。

5.5 优化调度

如果实现了很多个优化，那么就会意识到，不同的优化的执行顺序，是会对优化结果产生影响的，比如（没有遵循形式化表述）

$$2\sin^2(x)\cos(x)+2\cos^3(x)$$

如果先执行平方和化简

$$2\cos(x)$$

可如果先使用正弦二倍角化简

$$\sin(2x)\sin(x)+2\cos^3(x)$$

会发现结果由差异。所以怎么确定先采用哪个形式去化简呢？我反正没有实现这个事情，摆烂了。不过陈昊哥哥说可以用队列做，我昨晚又想了想，似乎这个具有后无效性？可以动态规划吗？甚至还可以加上时间的限制条件。反正我摆了，就不想了。

5.6 输出优化

标准项集合除了实现计算方法之外，最重要的就是实现 toString ,对于这里，有如下优化

• 把正项移到前面：1-x 优于 -x+1
• 系数为 1 或者 -1 的时候不输出系数：x 优于 1*x
• 指数为 0 的时候，不输出 x：1 优于 x**0
• 指数为 1 的时候，不输出指数：x 优于 x**1
• 项有负号的时候，不输出 +：-x 优于 +-x

---

六、评测机与 bug

6.1 组成

评测机由三部分组成：

• 数据生成器：用于生成测试数据
• 自动调用机：可以进行自动化的测试
• 检验机：可以用于检验正确性

6.2 数据生成器

6.2.1 原理

到了 6.3 终于可以贴合完整的命题空间了。其实生成数据的过程可以看做是解析的逆过程，基本上解析有几个函数，生成就有一个函数，这里放下 UML 图

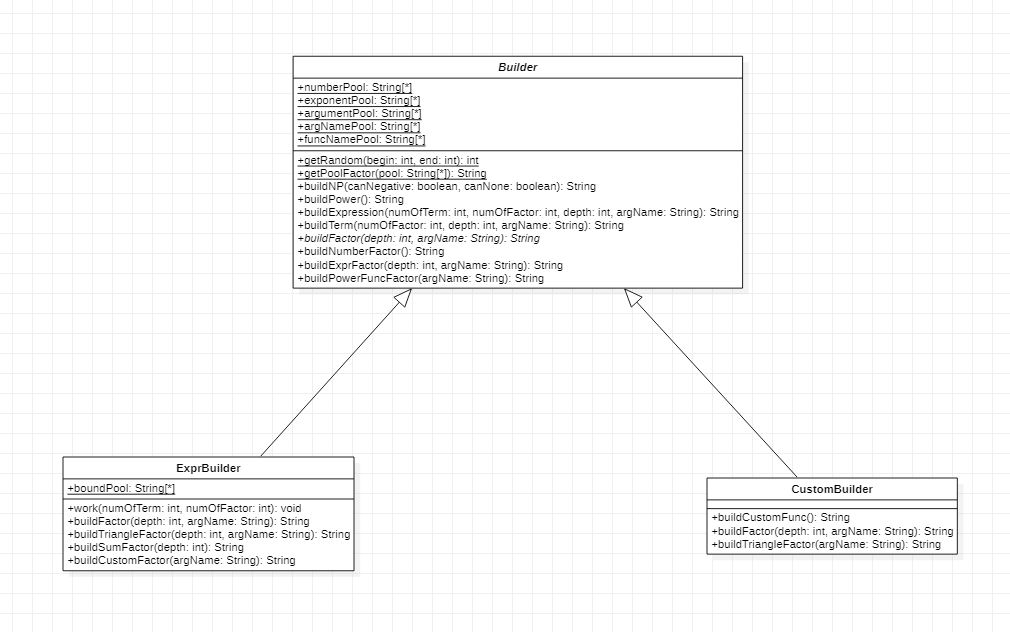
可以发现，基本跟 Parser 上一模一样。同样也是递归的创建。

6.2.2 复杂性控制

可以从两个方向控制：

• 项数和因子数，可以作为参数传入，控制循环的次数
• 递归深度，也可以作为参数传入，当调用某些方法的时候（比如创建表达式因子），就让深度减 1，当深度为 0 的时候，就限制一些构造的方法，比如禁止构造表达式因子

6.2.3 体验

我在第二次作业第一次写数据生成器，体验很不好，虽然领悟到了递归构造就是最贴切的构造方法，但是具体实现的时候，依然 bug 连连，最后还得重构，然后为了 debug，又给评测机写了一个评测机。

而且我意识到数据生成器只是评测机的一个组件，其他组件虽然对于不同的项目复用性会更高，但是依然是很体现技术的。而我当时年少轻狂，现在也是。总之吃了很多亏，干了很多费力不讨好的事情。

6.3 bug 分析

6.3.1 BigInteger

我这三次作业，强测都是满分，自己被 hack 了一次。出现的 bug 在 sum 的起始和终止都是 long 类型，而不是 BigInteger。我当时写的时候只考虑到因为长度限制，所以 begin 和 end 之间的差值不会超过 long，所以就图省事没有用 BigInteger ，但是没有想到起始和终止都是可以特别大的。

6.3.2 hack 策略

虽然写评测机的时候满心都以为可以用评测机发现别人的 bug，后来发现能 hack 到别人的数据都是手动构造的，尤其是还有一个构造是卡 TLE 的。我分析这是因为我写评测机的功力还不够，没有办法构造出特别刁钻的数据。还是以后多多参与，多多锻炼为好。

---

七、补充知识

7.1 对象处理流

总之就是深浅克隆问题，简单的定义就不说了。我做的时候一直在思考必要性，因为我第一次作业就没有用到 clone，所以影响我的是，我不知道如果浅克隆的会发生啥问题，反正大家都说有问题，我也不知道有啥问题。可能是因为我树上操作少，没有嫁接操作？总之就是因为没出过这个方面的bug，所以很难理解到底哪里有问题。第二次作业本来也不打算用 clone 的，但是想了想，还是改成有 clone 的交了。但是真的不明白会在哪里出问题，这可能跟我对于算法的需求不高有关。

但是还是担心的学了序列化和反序列化的知识，并用在了 clone 上，序列化和反序列化属于是对象处理流里的概念：

• 序列化就是保存数据的时候，保存数据的值和数据类型
• 反序列化就是在恢复数据时，恢复数据的值和数据类型
• 需要让某个对象支持序列化机制，则必须让其类是可序列化的。为了让某个类是可序列化的，该类必须实现如下两个接口之一（他的每个属性也必须实现这两个接口之一）
  • Serializable
  • Externalizable

我们用序列化反序列化实现 clone 的原理就是我们相当于是把对象保存到了一个文件中，然后立刻又从文件中把这个对象读了出来，此时这个新的对象就是一个深度 clone 的副本了。

这是标准写法

public class SerialCloneable implements Cloneable,Serializable  
{  
    public Object clone()  
    {  
        try  
        {  
            //save the object to a byte array  
            ByteArrayOutputStream bout = new ByteArrayOutputStream();  
            ObjectOutputStream out = new ObjectOutputStream(bout);  
            out.writeObject(this);  
            out.close();  

            //read a clone of the object from the byte array  
            ByteArrayInputStream bin = new ByteArrayInputStream(bout.toByteArray());  
            ObjectInputStream in = new ObjectInputStream(bin);  
            Object result = in.readObject();  
            in.close();  

            return result;  
        }
        catch(Exception e)  
        {  
            return null;    
        }  
    }  

}

我的写法，以标准项为例：

public PolyTerm clone()
{
    try
    {
        //save the object to a byte array
        ByteArrayOutputStream bout = new ByteArrayOutputStream();
        ObjectOutputStream out = new ObjectOutputStream(bout);
        out.writeObject(this);
        out.close();

        //read a clone of the object from the byte array
        ByteArrayInputStream bin = new ByteArrayInputStream(bout.toByteArray());
        ObjectInputStream in = new ObjectInputStream(bin);
        Object result = in.readObject();
        in.close();

        return (PolyTerm) result;
    }
    catch (Exception e)
    {
        return null;
    }
}

7.2 不可变类

看了讨论区赵姑娘的文章，感觉颇受启发，可能我的设计更偏向于不可变对象设计。赵姑娘主要讲了怎么实现不可变设计，我想对为啥不可变类可以解决 clone 问题。

这是我们容易出现的场景

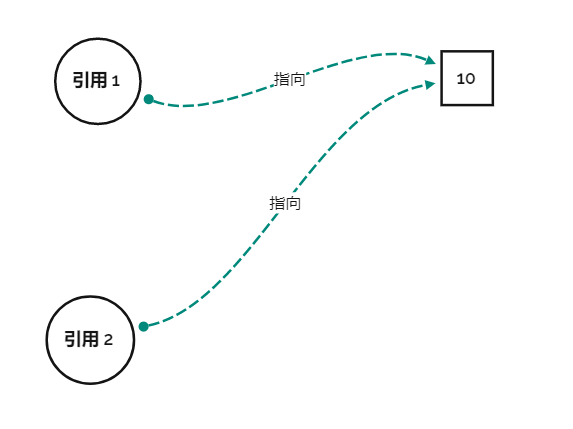
我看见这个场景就天生反感，因为这东西不是我想要的，我想要的是这个东西

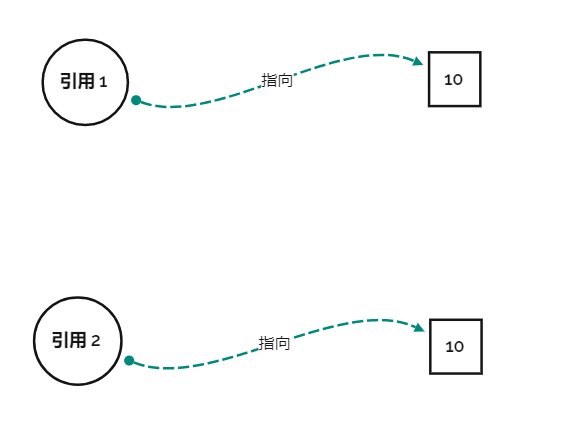
但是其实第一种图其实没啥不好的，只要不修改 10 的值，那么第一种就够了，就好像犯不着为每个人都配一个小便池，小便池能用就行了。我们对于厕所的问题，其实有人上完厕所不冲小便池，对应这里就是修改了 10 的值，只有这个时候我们会说，要是有独立卫浴就好了，这就对应了第二幅图的情况。

当我们使用了不可变对象的时候，就好像规定了人使用完小便池以后必须冲水，不然就枪毙他（保持对象的不可变性）。只要定下这个规矩，人们共享小便池的意愿就会高一些。

这是第一点，也就是说，不可变类减少了人们去 clone 对象的需求。就好像没人在有绝对干净的公厕时还会花钱修建个人卫浴（仅是比喻）。而另一点，如果真的有修改需求怎么办，我们如果用 clone 思想去做，是这样的

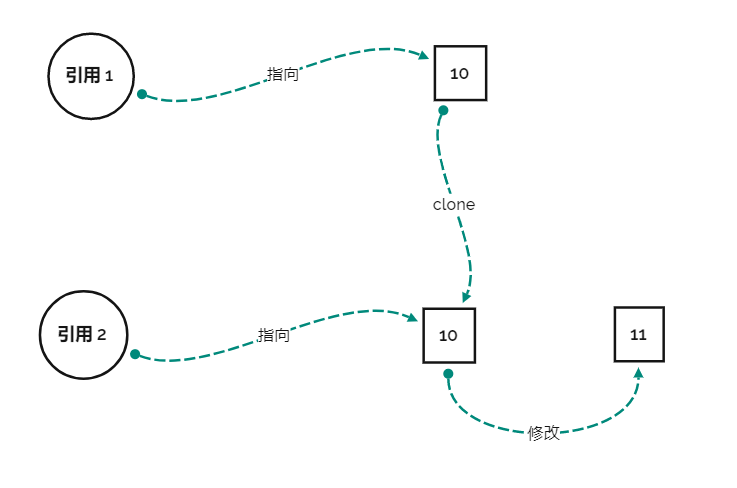
我们先 clone 出一个原对象，然后把值给修改了，就好像先仿造公厕里的小便池造一个小便池安自己家里，然后在给这个小便池镶上钻石来满足自己的品味需求。这时是需要 clone 的，因为如果不克隆，所有的人第二天上厕所的时候，都会发现自己居然会使用是一个镶钻石的小便池。

那么这种修改的请求不可变对象是如何处理的呢？如图

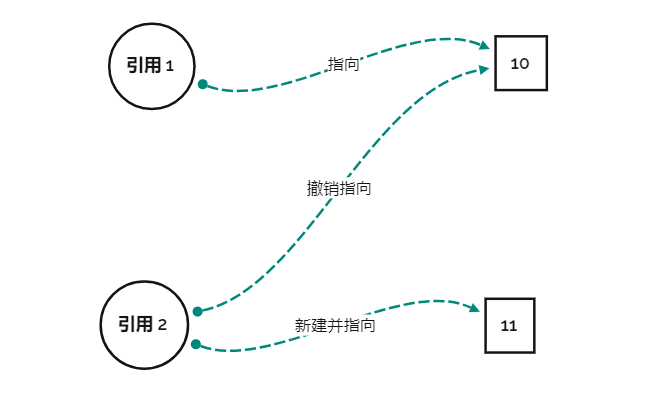
他直接新建了一个对象，然后对其进行了设置。就好像是现在开了一个新的公厕，这个公厕里的小便池是镶钻石的，现在这个高雅的人改去这个公厕了。相当于是将原来的“克隆并在克隆件上修改”，改成了“模仿原对象不需要修改的部分，结合需要修改的部分，重新建立一个新的对象”。

以上两种处理很好的满足了需求。

---

八、量化分析

8.1 基础知识

方法的衡量指标：

• CogC（Cognitive complexity）认知复杂度：衡量一个方法的控制流程有多困难去理解。具有高认知复杂度的方法将难以维护。sonar要求复杂度要在15以下。计算的大致思路是统计方法中控制流程语句的个数
• ev(G)（essential cyclomatic complexity）：方法的基本圈复杂度，衡量程序非结构化程度的。
• iv(G) （Design complexity）：设计复杂度
• v(G)（cyclomatic complexity）：方法的圈复杂度，衡量判断模块的复杂度。数值越高说明独立路径越多，测试完备的难度越大。

类的衡量指标：

• OCavg（Average opearation complexity）：平均操作复杂度
• OCmax（Maximum operation complexity）：最大操作复杂度
• WMC（Weighted method complexity）：加权方法复杂度

8.2 ast 包

方法分析

method	CogC	ev(G)	iv(G)	v(G)
ast.Add.addTerm(Node)	0.0	1.0	1.0	1.0
ast.Add.toPoly(HashMap)	1.0	1.0	2.0	2.0
ast.Custom.Custom(Node, HashMap)	0.0	1.0	1.0	1.0
ast.Custom.toPoly(HashMap)	0.0	1.0	1.0	1.0
ast.Multi.addFactor(Node)	0.0	1.0	1.0	1.0
ast.Multi.toPoly(HashMap)	1.0	1.0	2.0	2.0
ast.Num.Num(String)	0.0	1.0	1.0	1.0
ast.Num.toPoly(HashMap)	0.0	1.0	1.0	1.0
ast.Power.Power(Node, String)	0.0	1.0	1.0	1.0
ast.Power.toPoly(HashMap)	0.0	1.0	1.0	1.0
ast.Sum.Sum(String, String, Node)	0.0	1.0	1.0	1.0
ast.Sum.toPoly(HashMap)	1.0	1.0	2.0	2.0
ast.Triangle.toPoly(HashMap)	8.0	1.0	5.0	5.0
ast.Triangle.Triangle(String, Node)	3.0	1.0	3.0	3.0
ast.Variable.toPoly(HashMap)	2.0	1.0	2.0	2.0
ast.Variable.Variable(int)	1.0	1.0	1.0	5.0
ast.VarType.add()	1.0	5.0	1.0	5.0

分析：

可以看到所有的方法都很规矩，除了跟 Triangle 相关的方法。因为 Triangle 包括 Cos 和 Sin 两种，所以导致各种方法都需要写两个分支，然后相应的复杂度就上去了。之所以这样设计，是因为单独开设两个三角函数类，会出现大量的重复代码。修改起来也十分麻烦。如果再建立一个抽象类来提取公共代码，在利用多态来实现区别，应该是更好的设计思路。

类分析

class	OCavg	OCmax	WMC
ast.Add	2.6666666666666665	5.0	8.0
ast.Custom	1.3333333333333333	2.0	4.0
ast.Multi	3.0	6.0	9.0
ast.Num	1.3333333333333333	2.0	4.0
ast.Power	1.6666666666666667	3.0	5.0
ast.Sum	1.3333333333333333	2.0	4.0
ast.Triangle	4.0	5.0	8.0
ast.TriType			0.0
ast.Variable	4.333333333333333	6.0	13.0
ast.VarType	6.0	6.0	6.0

分析：

这个复杂度有些高啊，但是如果把这个里面的 toString 方法去掉，那么复杂度会大大减少。这里面其实 toString 方法没有用，就是我写出来用来调试的。所以其实这个复杂度还在可以接受的范围内。这里的分析也告诉我，不要把多功能集中在一个类上，而应该按照姜姐姐在研讨课上提供的思路单一职责。否则复杂度就会升高。

8.3 parser 包

方法分析

method	CogC	ev(G)	iv(G)	v(G)
parser.CustomParser.CustomParser(String)	0.0	1.0	1.0	1.0
parser.CustomParser.getExpr()	0.0	1.0	1.0	1.0
parser.CustomParser.getName()	0.0	1.0	1.0	1.0
parser.CustomParser.parseCustomFunc()	1.0	1.0	2.0	2.0
parser.CustomParser.parseFactor()	7.0	1.0	8.0	8.0
parser.CustomParser.parseVariable()	0.0	1.0	1.0	1.0
parser.ExprParser.addFunction(String)	0.0	1.0	1.0	1.0
parser.ExprParser.parseCustomFuncFactor()	1.0	1.0	2.0	2.0
parser.ExprParser.parseFactor()	10.0	1.0	11.0	11.0
parser.ExprParser.parseSumFactor()	0.0	1.0	1.0	1.0
parser.ExprParser.parseVariable()	3.0	1.0	2.0	3.0
parser.Lexer.getNumber()	2.0	1.0	3.0	3.0
parser.Lexer.Lexer(String)	0.0	1.0	1.0	1.0
parser.Lexer.next()	9.0	2.0	5.0	7.0
parser.Lexer.peek()	0.0	1.0	1.0	1.0
parser.Parser.getLexer()	0.0	1.0	1.0	1.0
parser.Parser.getNum()	2.0	1.0	3.0	3.0
parser.Parser.isInteger(String)	0.0	1.0	1.0	1.0
parser.Parser.parseExpression()	2.0	1.0	3.0	3.0
parser.Parser.parseExprFactor()	0.0	1.0	1.0	1.0
parser.Parser.parseFuncPowerFactor()	0.0	1.0	1.0	1.0
parser.Parser.parseNP()	2.0	1.0	3.0	3.0
parser.Parser.parsePower(Node)	2.0	1.0	2.0	2.0
parser.Parser.parseTerm(int)	1.0	1.0	2.0	2.0
parser.Parser.parseTriangle(String)	0.0	1.0	1.0	1.0
parser.Parser.setLexer(Lexer)	0.0	1.0	1.0	1.0

分析：

这里的设计就很好，各种方法的复杂度都很低，这是因为将大量的方法的内部再次进行拆解，拆解成了私有方法，这样大大降低了方法的复杂度。这个设计的技巧在之后的调试中也要用到。

类分析

class	OCavg	OCmax	WMC
parser.CustomParser	1.8333333333333333	5.0	11.0
parser.ExprParser	2.8	7.0	14.0
parser.Lexer	2.75	7.0	11.0
parser.Parser	1.5454545454545454	3.0	17.0

分析：

这些类的复杂度都比之前 ast 包的类的复杂度高一些。这应该是是这些类的功能更多的原因。但是用私有方法的方式，可以方便的定义bug。

8.4 poly 包

method	CogC	ev(G)	iv(G)	v(G)
poly.Polynomial.multi(Polynomial)	3.0	1.0	3.0	3.0
poly.Polynomial.negative()	1.0	1.0	2.0	2.0
poly.Polynomial.Polynomial()	0.0	1.0	1.0	1.0
poly.Polynomial.power(long, Polynomial)	1.0	1.0	2.0	2.0
poly.Polynomial.removeIfZero()	0.0	1.0	1.0	1.0
poly.Polynomial.selectShortest()	4.0	1.0	4.0	5.0
poly.Polynomial.simplify()	0.0	1.0	1.0	1.0
poly.Polynomial.squareTrans(TriType)	1.0	1.0	2.0	2.0
poly.Polynomial.toString()	7.0	1.0	4.0	5.0
poly.Polynomial.traverse(Polynomial, TriType)	2.0	1.0	2.0	2.0
poly.PolyTerm.clone()	1.0	1.0	1.0	2.0
poly.PolyTerm.equals(Object)	4.0	3.0	5.0	7.0
poly.PolyTerm.getCoefficient()	0.0	1.0	1.0	1.0
poly.PolyTerm.hashCode()	0.0	1.0	1.0	1.0
poly.PolyTerm.isFactor()	6.0	4.0	7.0	10.0
poly.PolyTerm.isSameType(PolyTerm)	3.0	2.0	4.0	4.0
poly.PolyTerm.isSameTypeRough(PolyTerm)	24.0	10.0	14.0	19.0
poly.PolyTerm.isZero()	7.0	4.0	3.0	4.0
poly.PolyTerm.multi(PolyTerm)	13.0	1.0	8.0	8.0
poly.PolyTerm.PolyTerm(BigInteger, BigInteger)	0.0	1.0	1.0	1.0
poly.PolyTerm.setCoefficient(BigInteger)	0.0	1.0	1.0	1.0
poly.PolyTerm.setCos(HashMap)	0.0	1.0	1.0	1.0
poly.PolyTerm.setSin(HashMap)	0.0	1.0	1.0	1.0
poly.PolyTerm.squareTrans(TriType)	6.0	1.0	4.0	5.0
poly.PolyTerm.toPoly()	0.0	1.0	1.0	1.0
poly.PolyTerm.toString()	17.0	2.0	8.0	8.0
poly.PolyTerm.triangleToString(HashMap, String)	11.0	1.0	5.0	5.0

分析：

这个包里的方法的复杂度都偏高，这是因为这里的方法不是优化，就是输出，为了性能分，大量的引入了各种特判条件，导致了复杂度提高。这里其实也揭示了一个道理，就是优化性能有可能导致正确性的牺牲。或者说复杂就容易失误。这样的话，简洁优秀的算法，就是一个很好的设计目标。

类分析

class	OCavg	OCmax	WMC
poly.Polynomial	2.3333333333333335	5.0	49.0
poly.PolyTerm	3.4705882352941178	12.0	59.0

分析：

感觉是因为方法的调用次数，导致了加权偏高。我曾经考虑过单独做出一个包来分担优化的功能。但是设计能力有限，遗漏了这个设计。

---

九、迭代

其实怎么说呢，虽然我觉得我第一次架构就可以应付三次的作业。但是我最为骄傲的就是，每次我都是重构的，虽然这些重构并不是对架构的调整，但是我尽量在重构的过程中将代码写的更加简洁优雅。

在第二次作业中，我把原来的 Expression、Term、Factor 类都去掉，换成了更为抽象的 Node。这个重构使架构中的树结构更加明显。

在第三次作业中，我把 Parser 作为一个抽象类，这样减少了重复代码量，而且更加贯彻面向对象的思想。

---

十、鸣谢

首先最最应该感谢的人就是李寻欢，可以说真的真的对我的帮助很大。我第一单元的所有设计，都是对李寻欢设计思想拙劣的模仿。似乎给我画出了我这种实力的破学生的设计的极限。每每我恍然大悟，就发现李寻欢早已在那里等着我。

不仅是设计方面，李寻欢设计中透露的那种粗粝的美感，那种果决与英气，都是我不具有的，可以说李寻欢在我进入 OO 这门课初，塑造了我对于项目的审美。

其次感谢郭嵩阳，在我深陷困难的时候及时帮忙，感谢至极。

最后感谢我的其他朋友们，他们或多或少在我的实践中为我提供了帮助。感谢之至。