随机变量的函数就是说通过函数映射的形式,将原来的一个或者多个随机变量放进函数里,然后得到一个新的随机变量。这里主要是分成了两种类型,一个是一元函数,另一个是多元函数(基本上都是二元函数)。这两种函数因为诞生的意义的不同,所以在研究方法和其他方面里都存在明显的差距。
对于一元函数,我觉得最漂亮的是关于标准分布的构造。这个思想是我见过构造性最强的数学应用,总之就是很漂亮的构造。
对于二元函数,会涉及到两个随机变量的相互作用,所以应用的数学工具会更加强大,比如说卷积,线积分,可以说是另一个层次的美感。
一、分布分类
正如摘要提到的,分布的描述对象不止限于客观对象。因此我们对现在研究的分布进行一个分类:
| 类别 | 分布 |
|---|---|
| 普通分布 | 正态分布,负指数分布,均匀分布等 |
| 标准分布 | 标准正态分布, $\chi^2$ 分布,$t$ 分布,$F$ 分布 |
理解这补充的三种分布,最重要的是,本质上他们都普普通通的分布,与正态分布,负指数分布,均匀分布没有任何区别。我们对普通的分布,研究的是数字特征,研究他们的性质,对于标准分布,我们依然研究他们的参数,研究他们的性质。
当然,区别还是有的,他们与普通分布的最重要区别是,他们一般不是对客观世界某个试验的结果的描述,比如说负指数分布可以描述动物的寿命,服务系统的排队时间,正态分布可以描述人群的身高。但是这些标准分布并不能描述自然现象,也就是普通的随机变量,他们描述的是随机变量的函数,换句话说,他们描述的是对象是经过数学构造过的随机变量。所以他们的概率密度的数学形式更加复杂,而且莫名其妙,不容易让人理解。
那么我们为什么要这样自讨苦吃?好在了我们完全了解标准分布,我们知道他们的密度函数表达式是什么,虽然分布函数的表达式写不出来,但是我们有表,就等于知道了所有的概率分布。如果一个随机变量服从这些标准分布,我们就完全了解了这些随机变量,我们想求一个区间的概率密度,一查表,事情就解决了。
另外还有一个重要特点,就是标准分布呈现了连续构造的特征,我们构造 $\chi^2$ 分布的时候利用了 $\phi$ ,构造 $t$ 分布的时候利用了 $\chi^2$ 和 $\phi$ ,构造 $F$ 分布的时候利用了 $\chi^2$ 。但是需要注意,虽然构造的时候,分布们互相调用,但是这种调用也没有办法看出任何有意义的联系。这种构造方式,一般是为了说明某个随机变量是随机变量,也就是说,发挥的是判定定理的作用。
二、标准分布
2.1 标准化随机变量
虽然这个不是标准分布,但是他的精神是一致的,就是不再描述客观世界中的随机变量,而是描述用函数构造出的随机变量。
对于随机变量 $X$ 构造 $X^*$
这个新的标准化随机变量,有以下数字特征:
2.2 标准正态分布
参数 $\mu = 0, \sigma = 1$ 的正态分布即 $N(0,1)$ ,被称为标准正态分布,其概率密度函数和分布函数分别用 $\phi(x)$ 和 $\Phi(x)$ 表示。
之所以提出标准正态分布的概念,是因为为了方便实践,虽然正态分布函数没法用初等函数表示,但是我们可以通过查表来获得标准正态分布某个区间的概率。只要我们能在正态分布函数和标准正态分布函数中建立某种联系,我们就可以获得所有正态分布的区间概率。
在后面的介绍中,即使这些标准分布都可以给出概率密度的表达式,但是我都不记录,因为没必要,因为我们也不会对其积分,我们算概率用的是查表。
应用:
2.3 $\chi^2$ 分布
判定:
若$X1, X_2, X_3, \cdots, X_n, \cdots$ 相互独立,且都服从 $N(0,1)$ ,则随机变量 $\sum^n{i = 1}X_i^2$ 服从 $\chi^2(n)$ 分布。
性质:
- 有一个参数n,当n越大的时候,概率密度图像越平,最高点越向 x 轴正方向延伸
- 若 $X\sim \chi^2(n)$ ,有 $EX = n, DX = 2n$
- 若 $X_1\sim \chi^2(n_1)$ , $X_2\sim \chi^2(n_2)$ ,则 $X_1 + X_2 \sim \chi^2(n_1 + n_2)$
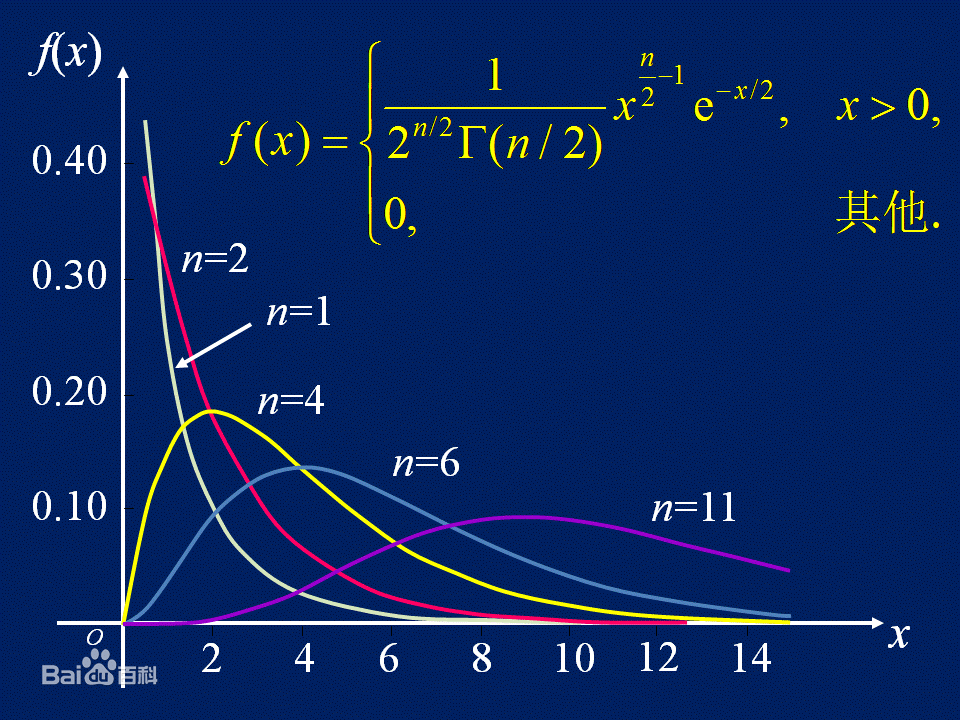
应用:
除了上面这个应用以外(也就是获得 $\sigma$ 的置信区间),卡方分布还有一个重要应用是检验总体分布假设(这是我们高中就接触的),其原理是皮尔逊 $\chi^2$ 统计量,这种统计量服从 $\chi^2$ 分布。
其中我们需要将数轴分为 $k$ 个不相交的区间(如果是离散型,那么离散型随机变量有几个取值,就分几个就好了),这种说法应该是为了连续型随机变量,$p_i$ 是这些区间的理论概率,$n_i$ 是试验落在对应区间的个数。
2.4 $t$ 分布
判定:
若 $X \sim N(0,1), Y \sim \chi^2(n)$ ,且 $X,Y$ 相互独立,则 $\frac{X}{\sqrt{Y/n}}$ 服从 $t(n)$ 分布。
性质:
- $t$ 分布关于 $t = 0$ 对称
- 当 $n\rightarrow +\infty$ 时, $t$ 分布近似于 $N(0,1)$ ,当 n 较小的时候, $t$ 分布与正态分布有较大差异
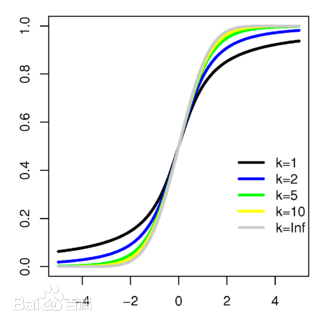
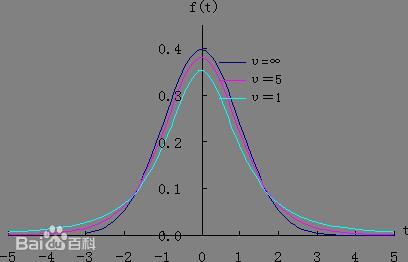
应用:
2.5 $F$ 分布
判定:
若 $X \sim \chi^2(n_1), Y \sim \chi^2(n_2)$ ,且 $X,Y$ 相互独立,则 $\frac{X/n_1}{Y/n_2}$ 服从 $F(n_1, n_2)$ 分布
性质:
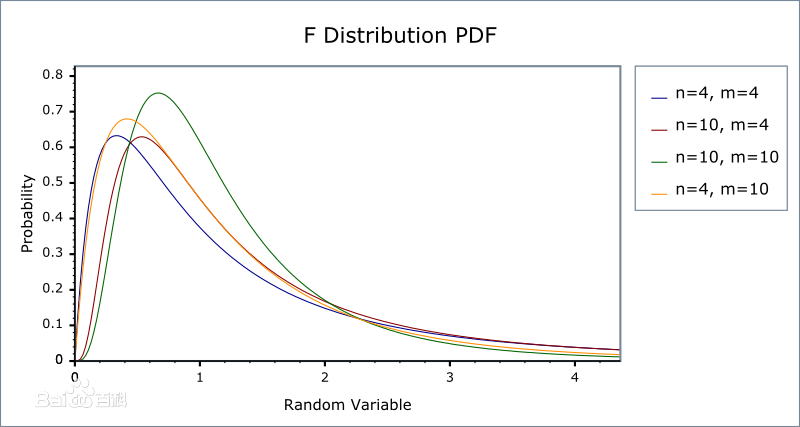
应用:
三、连续型随机变量的函数的分布
3.1 一维分布
这就是我觉得简单的那种,其关键点在于一个反函数,就直接拆开就好了,不会太难的。
3.2 二维分布
3.2.1 一般方法
已知二维连续型随机变量 $(X,Y)$ 的概率密度为 $f(x,y)$。求 $Z = g(X,Y)$ 的概率密度。
解:计 $D_z = {(x,y)\mid g(x,y)\le z}$。
3.2.2 $Z = X + Y$
做变量代换 $y = t - x$,然后有
所以有 $Z$ 的概率密度为
当然,如果是更加普世一点的 $Z = aX + bY +c$,有
其中 $\bar{AB}$ 是 $z = ax + by + c$ 这条直线的有向线段。相当于是一种第二类曲线积分。
如果有 $X,Y$ 是相互独立的条件,那么就会有更加优雅的结论,那就是
我们又管右端的积分叫做卷积(关于卷积,可以看我的其他博文有介绍)
如果独立的变量还是正态分布,那么我们还有更好的性质,即
如果我们有 $X_i\sim N(\mu_i,\sigma_i^2)$ 。且各个随机变量相互独立,那么有
3.3 $Z = max{X,Y}$
已知二维连续型随机变量 $(X,Y)$ 的概率密度为 $f(x,y)$,分布函数是 $F(x,y)$。
如果有 $X,Y$ 是相互独立的条件,有
3.4 $Z = min{X,Y}$
已知二维连续型随机变量 $(X,Y)$ 的概率密度为 $f(x,y)$,分布函数是 $F(x,y)$。
同时也有:
如果有 $X,Y$ 是相互独立的条件,有