数学建模-贷款问题

一、例子

之后的所有讲解，都是基于这个例子的，所以在头部统一列出

假定某消费者购房需要贷款 30 万元，期限为 30 年，已知贷款年利率为 5.1%，问每月应还款多少？

符号约定如下

利率的计算是很反人类的，他是被“线性处理”的，也就是说，对于年利率 5.1%，月利率和日利率分别如下计算

$r_{y} = 5.1\%\\ r_{m} = r_{y} \div 12 = 0.425\% \\ r_{d} = r_{y} \div 30 = 0.0142\%$

是直接可以除的，但是这样产生的利息却不是线性的，我们以一年为例，如果按照一年为周期，贷款是 1 去计算，那么产生的利息就是

$(1 + r) - 1 = r$

但是如果是以半年为周期，那么产生的利息就是

$(1 + \frac{r}{2})^2 - 1 = r + \frac{r^2}{4}$

就是多于按照一年为周期去计算的利息，这是因为在第一个半年产生的利息会利滚利式地在第二个半年产生利息。

设在一年中总共“均匀地”还款 $x$ 次，那么对于利息总额，就有

$(1 + \frac{r}{x})^x - 1$

取极限

$e^r - 1$

所以直观的理解就是不要无限分割，越分割就会导致利息越多。所以在黑社会借贷中，经常出现“日利息，将一个月还清变成半年还清”的手段，这样会导致利息直线上升。

在实际生活中，我们一般按照一个月为还款周期，所以每月 0.425% 和一年 5.1% 差异还是很大的。

所谓等额本金，就是在每个月都会偿还等额的本金，同时偿还还未偿还的本金产生的利息，也就是对于第 $i$ 个月，有如下公式

$x_i = \frac{Q}{N} + (Q - (i - 1)\frac{Q}{N}) \times r = Q \times (\frac{1 + (N + 1)r}{N} - \frac{r}{N}i)$

在此题中，$x_i = 2111.875- 3.54i$ ，也就是每个月最多还 $2111.875$元，最少还款 836.875 元。

可以看出每月的还款金额形成一个等差数列，每个月减少 $\frac{Qr}{N}$ 。最终的还款的总额是

$Q \times (1 + \frac{N + 1}{2}r)$

也就是利息是

$Q \times \frac{N + 1}{2} r$

在此例中为 $230137.5$ 元。也就是 23 万元，是本金的 $\frac{2}{3}$ 。

等额本息指的是每个月还款的额度是相同的，那么就有如下差分方程

$y_{i + 1} = (1 + r) \times y_n - x \\ y_0 = Q$

可以直接递推求出

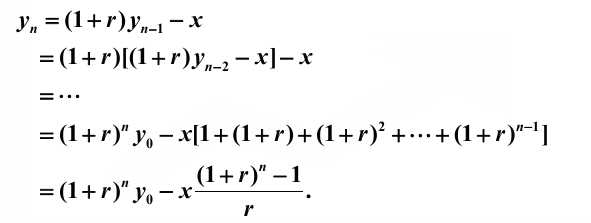
再结合条件 $y_N = 0$ ，可以求出

$x = \frac{(1 + r)^NQr}{(1 + r)^N - 1}$

带入本题数据可以计算每月需要还款 $1628.85$ 元，最后总利息为 $286386$ 元，也就是 26 万元。

这种方法会相比于等额本金，会导致需要偿还的利息更多，而且基本上越是长期的存款，即 $N$ 越大，这个效果越明显。但是因为其每月还款金额固定，且在一开始的时候每月的还款金额是小于等额本金的，所以对于大型贷款，我们一般选择这种方式。

至于为什么会还的钱更多，是因为我们在一开始，没有偿还更多的钱，导致我们让更多的利息产生了“利滚利”的效应。

先息后本名义上是“先还利息，后还本金”，每个月需要归还的利息是

$Qr$

在换完 $N$ 个周期后，最后再支付 $Q$ 的本金，那么在此题中，总利息就是 $QNr = 459000$ 元，也就是 45 万元。这种方式每个月只需要偿还利息，所以是不需要付本金的，所以还款的方式可以更加灵活，资金流转更加畅通。