一、系统结构设计
1.1 体系结构
1.1.1 总体结构
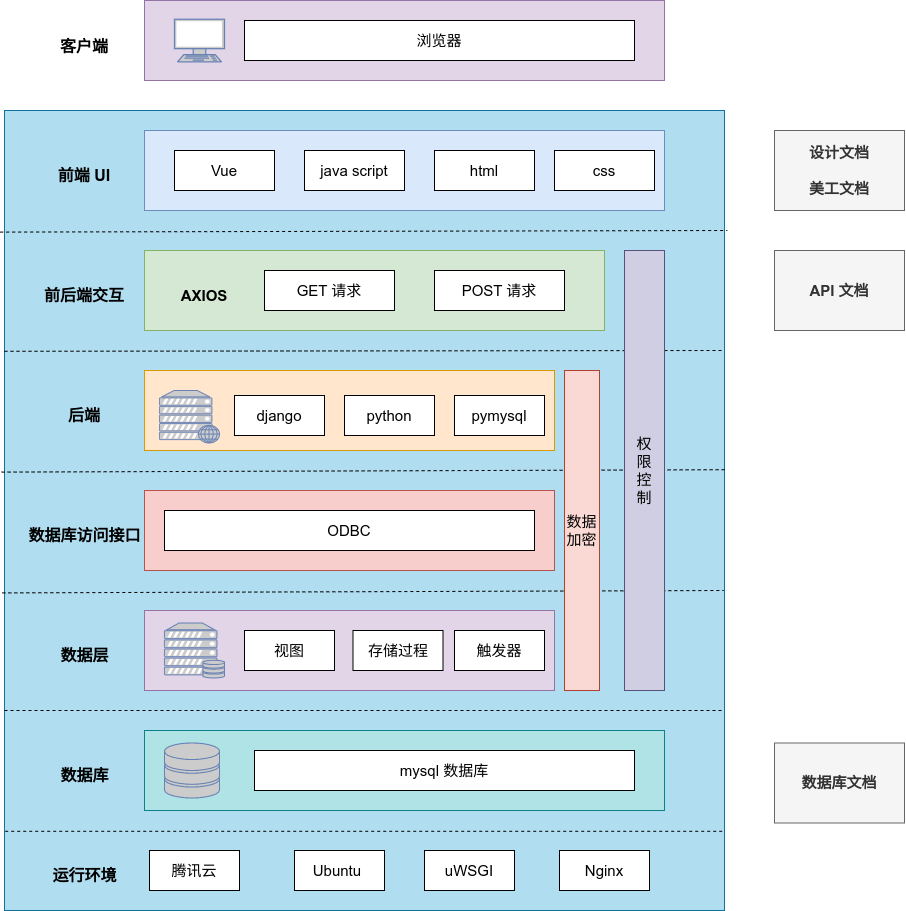
项目的整体架构如图所示
第八次全国学生体质与健康调研结果显示,大学生体质下滑的问题,仍然没有得到有效遏制。高校体育如何从世界百年未有之大变局和中华民族伟大复兴战略全局中认识新机遇、洞察新挑战、顺应新变化?高校体育如何担起培养社会主义现代化强国的建设者和接班人的伟大使命?作为为祖国培养“健康工作七十年的红色工程师”的北京航空航天大学,应当以怎样的技术和平台来支持学生体育事业。这些问题都值得我们深入思考。
首先,应当意识到,高校体育是一个完整的生态闭环,体育课程,体育比赛,官方体育活动,社团活动等都是高校体育建设不可或缺的一部分。高校体育建设不应当仅仅局限于每周固定时长的体育课程,恰恰相反,他应当融入大学生的生活中。也就是构建“立体化”的高校体育体系,拓展大学体育课程体系的长度、宽度和高度。学校体育课程要为学生走向社会和未来生活做准备,让大学生掌握体育知识、运动技能并能运用于生活之中,保持健康的体魄,促进自己的全面发展,帮助大学生适应未来,引导大学生创造未来。
llvm 是 SSA 形式的,但是在没有经过 mem2reg 的时候,SSA 是内存形式的,也就是说,对于每个变量,只要在定义他的时候,为他在内存中划分空间存入,在使用他的时候在取出来,这样就可以达到 SSA 的效果。这是因为 SSA 只要求我们不能改变一个已经定义的值,改变内存的内容显然并不违法 SSA。
这会导致当我们提到(也就是查询)一个局部变量的时候,其实是从符号表中取出来的是它的指针,这个过程一般发生在 LVal。一般我们会对变量干两件事情,读变量和写变量和做实参。对于读变量,一般发生在 LVal 作为 PrimaryExp 的时候发生,此时需要在 PrimaryExp 中对其进行 Load,而写变量一般发生在 LVal 在 AssignStmt 和 InStmt 中,只需要用 Store 将其写入即可。做实参要单独挑出来讲,是因为它的逻辑是与 C 需要保持一致的,他是有指针类型的,这就要求我们对他进行单独的处理。这就是内存式 SSA 的基本逻辑。