一、总论
单纯形法十分神奇,涉及的理论并不困难,但是很复杂。而且不但理论繁琐,而且算法有变得极具有“跳大神色彩”,“单纯性表、检验系数”等一系列玄学名词让人作呕(从我和我妈打交道的经历来看,经济学一定说一些非人话的东西,才可以满意)。更加痛苦的是,它是线性代数知识的应用,我对于线代的理解就是,“挟泰山以超北海”,很多复杂的东西被用线代知识简化成了“魔数”一样的东西,课本并不会详细说为啥是这样的,他们只会说大概可以用线代知识表示成这样。
二、线代知识复习
对于一个线性方程组,我们可以将其转换成矩阵形式,也就是
的形式,其中我们对于 $A$ 的考察变得很有趣,如果 $A$ 是一个满秩矩阵,那么就很容易,必然存在唯一解 $x$。但是如果 $A$ 不是满秩的,那么它就会导致 $x$ 是多解的,多解就意味着有一个解空间,不幸的是,这个解空间都是可以求的(所以才这么多麻烦事)。
对于 $Ax = b$ 的求解,首先是解出一个特解来。特解需要先利用高斯消元来化简矩阵为阶梯矩阵,然后变成阶梯矩阵之后,就可以很容易将阶梯角的列向量挑出来,他们对应的解的分量是必须的,对于非阶梯的地方,我们就让他们对应的解的分量为 0 ,然后就可以解出特解来了。
然后我们求出 $Ax = 0$ 的解平面,然后就可以“通解 + 特解”了。这个部分我写的很潦草,是因为我本来就不具备把他写好的能力。
之所以复习这里,是因为线性规划设计到的就是一个 $Ax = b$ 形式的方程,而且其中 $A$ 不满秩,这才导致 $x$ 具有多解,而线性规划描述的,正是在这多个解中,调出我们需要的那个最优解 $x_0$ 的事情。
三、线性规划原理
让我们关注本质,忽略一下如何把不太规范的线性规划转换成规范的线性规划,我们直接看规范的线性规范,描述的是这样的一个东西,有 $Ax = b, x > 0$ 的约束条件(同时有 $A$ 不满秩,满秩就直接解出来 $x$ 了),要求 $z = cx$ 的最大值或者最小值。
然后经过某个神秘的定理,我们获得了一个有用的信息,就是 $x$ 虽然可以取很无数个值,但是有可能是最优解,只会发生在某些特定的情况下,当我们解线性方程组特解的时候,用到了这个方法
就可以很容易将阶梯角的列向量挑出来,他们对应的解的分量是必须的,对于非阶梯的地方,我们就让他们对应的解的分量为 0 ,然后就可以解出特解来了
概括一下就是,因为 $A$ 不满秩,所以可以拆成一个满秩的矩阵(基向量组),和一堆非基向量,然后让非基向量对应的变量为 0,就可以求出特解。但是非基向量是被挑出来的,有很多种挑法,这就导致会有很多的特解。我们的定理告诉我们
最优解一定在这堆特解中。
如果 $A$ 是 $m\times n$ 维的,那么这堆特解的个数就是 $C^{m}_{n}$ 个。我们只要尝试了这么多次,就可以把这个问题解决了。但是显然这太愚蠢了。所以我们发明了单纯形法,这个方法可以让我们更快的找到最优解。
四、单纯形法
在开始介绍单纯形法之前,一定要强调,我并没有完全弄懂这个东西,哪怕跳过了证明,但看思路,也是没有完全弄懂,所以我不认为在期末的时候,我可以把他搞懂。
单纯形法就是靠着不断的换入和换出基变量,来最终确定那个最优解的基变量组的。我们首先挑选出“入基变量”,根据的是将 $z$ 表达成只含非基变量的线性表达式完成的,然后通过判断非基变量前系数的正负来判断各种东西。至于为啥可以,虽然书上解释了一大堆,但是我没有看懂,而且我觉得看不懂了。至于这个前面的系数,被称作检验数 $\sigma$ 。
可以再补充一下,这个检验数可以看做是用基变量表示目标函数的时候,基变量前的系数(鬼知道为什么要故弄玄虚),之所以叫做检验数,是因为它可以判断这个算法是否终结(这也很显然,当系数都为负数或者都为正数的时候,就该停止了)。
这里插入一段,我跟香老师说了这件事情,香老师帮我解释清楚了。
我们的 $z$ 长成这样
我们可以通过 $Ax = b$ 这个关系,用非基变量表示基变量,变成这种东西
但是我们又约定了,非基变量只能是 0,所以这次的 $z$ 的取值就是 $c^{‘}$ 。我们如果不让某个非基变量为 0,那么 $z$ 可以更大,但是我们让其不为零的方法就是让它称为基变量。也就是“换入”。
其次确定“出基变量”,根据的是一个叫做 $\theta$ 规则的东西,说白了就是让所有的基变量都为 0,进而求出入基变量的最大值,我们当然希望入基变量越大越好,但是无限制的大会导致其他基变量的取值变成负数,这就不符合题义了。所以我们才让所有的基变量为 0(可以被看做是负数的边界),然后去求 $\theta$,我们会挑出“非负的,最小的”(很容易想到为什么是这个条件)的 $\theta$ 对应的基变量,然后让它成为非基变量。
此外,对于求解最大值和最小值的问题,其实需要修改的只有对于 $\sigma$ 的判断,并不涉及对于 $\theta$ 判断规则的改变,这也是非常显然的事情。
然后经过这么愚蠢的直观理解后,到了记录单纯形法过程的环节。
五、实现
首先看题面
我们根据这个表可以填出下面这张表
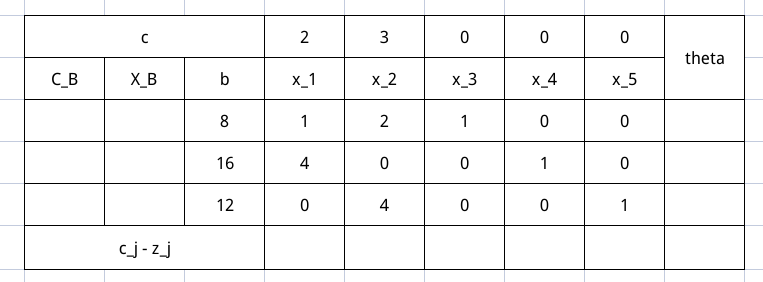
其中最上面 c 这一列表示变量的价值系数,就是 $max \space z = 2x_1 + 3x_2 + 0x_3 + 0x_4 + 0x_5$ 各个 $x$ 前各个系数,这里写定了就不会变了
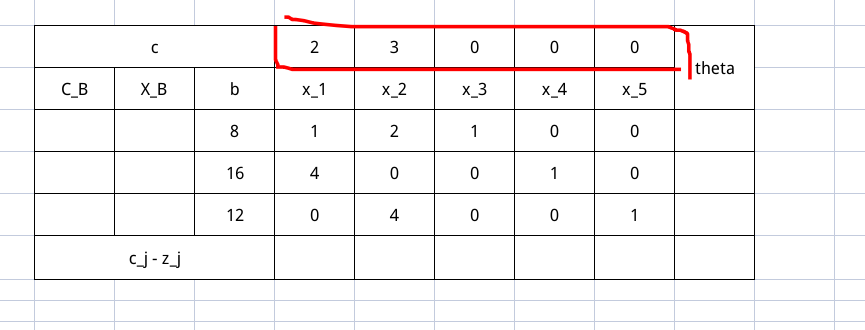
底下是一个增广矩阵,之后的入基操作和出基操作本质都是行变换,这个部分就是行变换的部分,就是需要跟着行更新的东西。
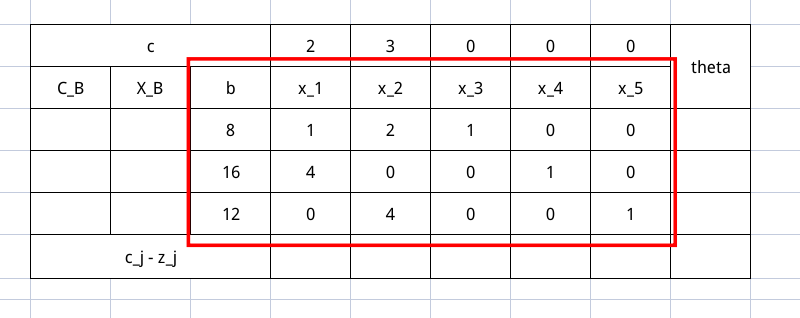
然后我们来填写一下基向量部分,在这个表里,下标是 $B$ 的量,都是与基向量有关的。从图可知道,基向量是 $x_3, x_4, x_5$ 。$X_B$ 这一项说明了这个东西
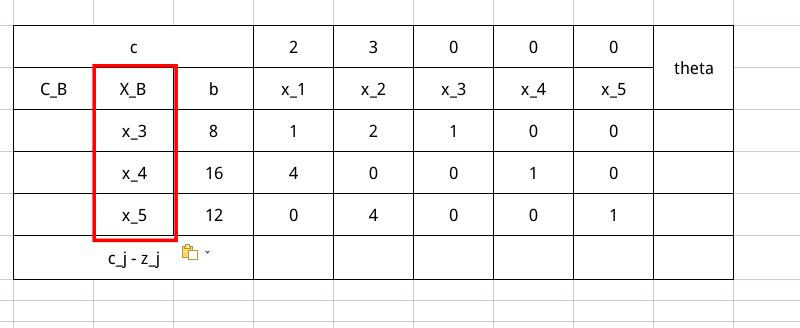
$C_B$ 这一项是 $X_B$ 各个分量对应的价值系数,是随着 $X_B$ 变化的。
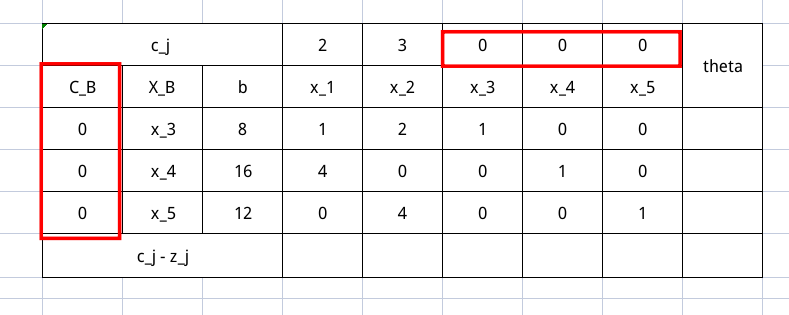
然后这个表里所有直观的东西就都填完了,现在我们要计算 $\theta_j$ ,$j$ 下标的意思就是每列(也就是每个变量)都会有这样的一个东西。其计算公式是
$c_j$ 是价值系数,很显然,$z_j$ 就没有那么直观,它本质是用非基变量代替基变量的过程,发生了系数的改变,其算式是 $z_j = C_B P_j^{T}$ 。也就是这下面两个变量的相乘
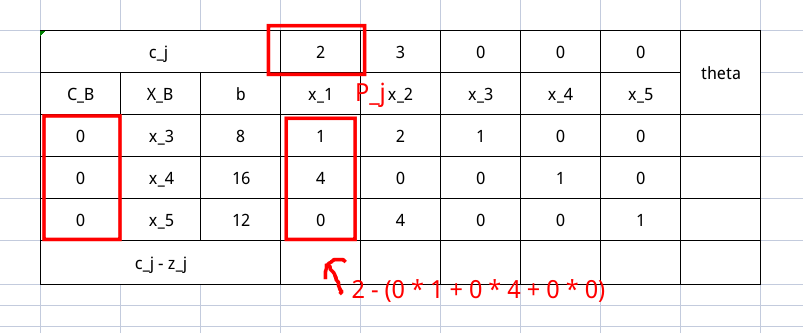
按照这个规则将 $\sigma_j$ 填好,有如下示例
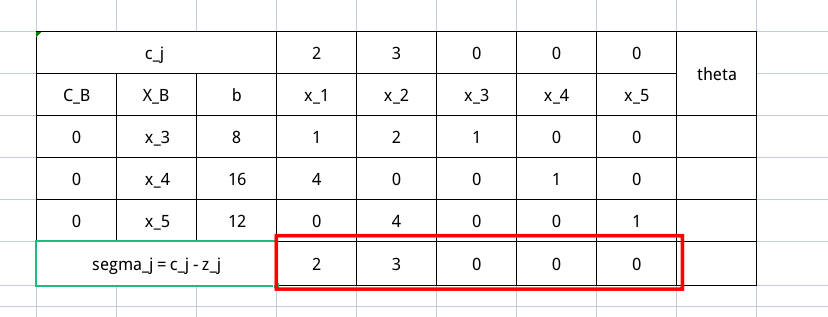
然后就必须审视一遍所有的 $\sigma$ ,如果所有的 $\sigma$ 都小于等于 0,事情就结束了。如果没有,那么我们就需要看看所有的非基变量对应的列向量 $P_j$ ,如果存在某个 $P_j \leq 0$ 。那么这个问题是无界的,否则就可以进行下一步了。
我们挑出 $\sigma$ 最大的那个非基变量,他就是入基变量了。在这道题中,就是 $x_2$
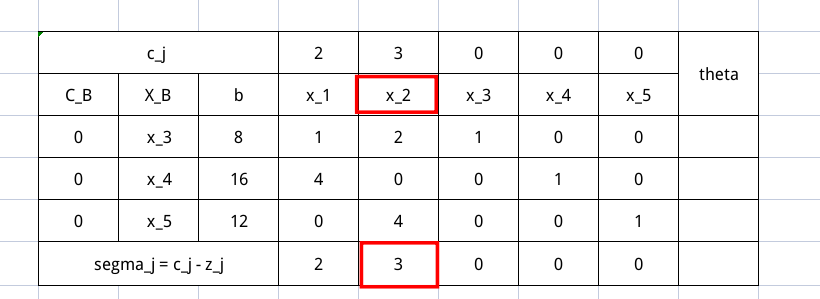
我们需要根据入基变量 $x_2$,确定出基变量,确定方法就是利用 $\theta$ ,计算方法是 $\theta = b \div P_2$ 。其中 $\div$ 是对应项相除的意思,有
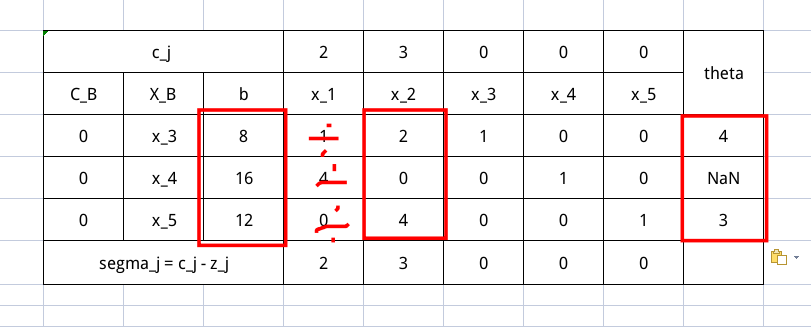
然后我们需要挑出最小的 $\theta$ ,找到对应的基变量,也就是 $x_5$ 。这就是出基变量
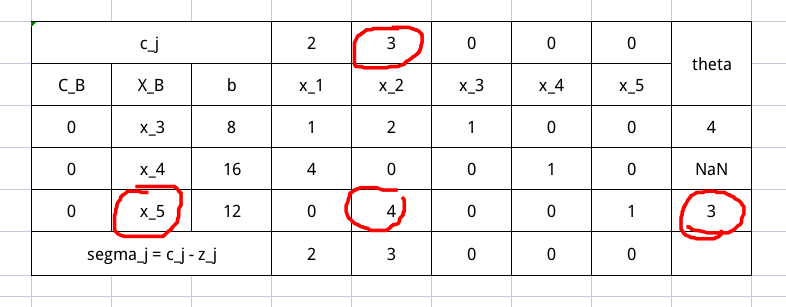
现在我们确定了出基变量 $x_5$ 和入基变量 $x_2$ 。现在需要利用行变换知识将其一个转换为基变量,另一个就顺其自然变成了非基变量。
首先归一化
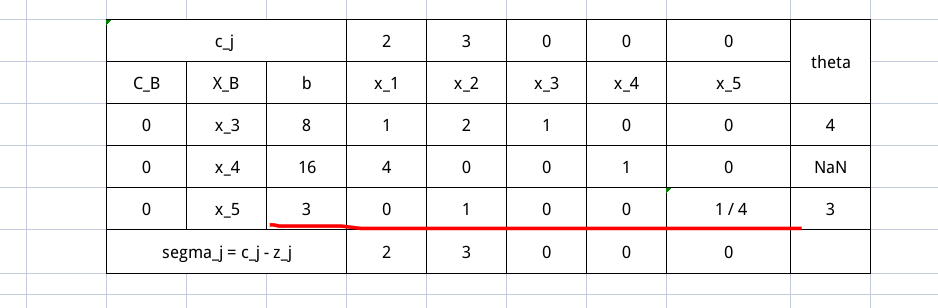
然后将 $P_2$ 其他分量都搞成 0,即
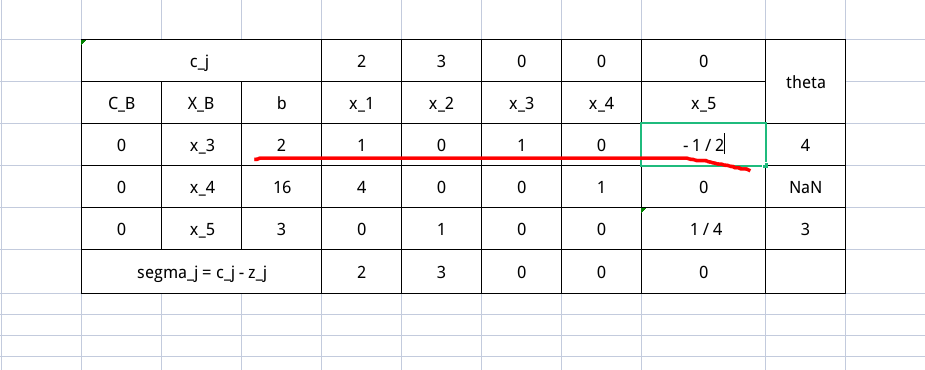
因为基向量发生了改变,所以建立在其上的 $X_B, C_B, \sigma_j, \theta$ 都需要重新计算,也就是下面这张表
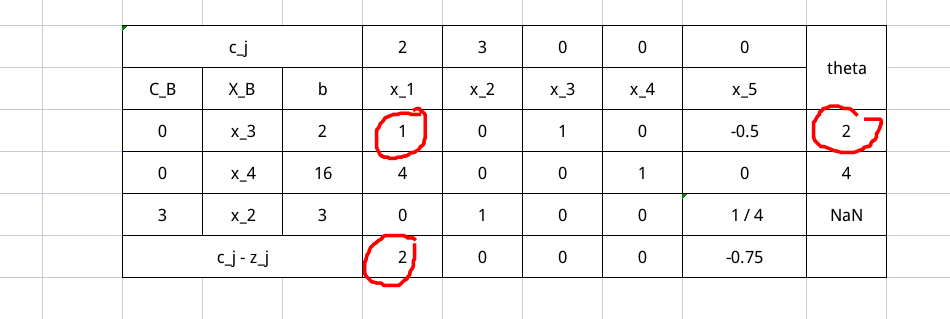
入基变量是 $x_1$ 出基变量是 $x_3$ 。然后继续进行行变换,并且更新 $X_B, C_B, \sigma_j, \theta$ ,有
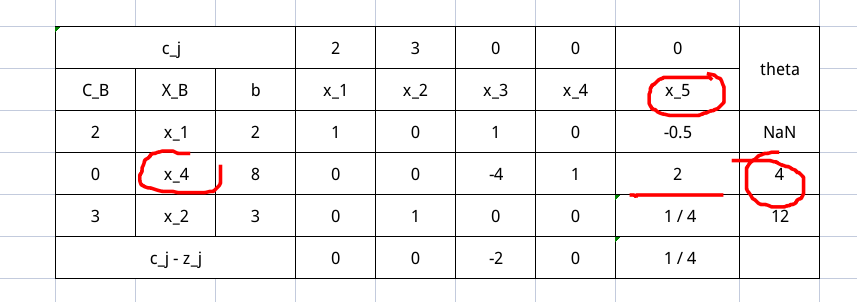
继续迭代
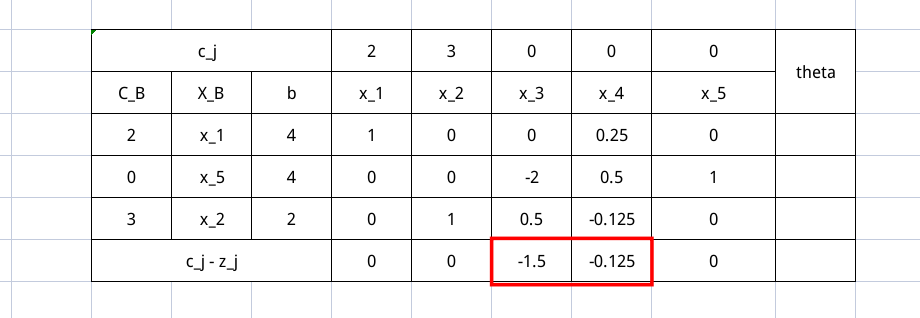
计算完 $\sigma$ 之后就会发现均为负数,所以就可以停止迭代了,冷知识,现在的 $b$ 值就是我们 $(x_1, x_5, x_2)$ 的值。
六、课设实现
课设实现相较于原有实现要更加简单,表项更少,但是并没有实际降低算法的难度,所以实际效果是一样的。课设删掉了 $\theta$ 这一列,并且将 $b$ 这一列移到了最右侧,这个是我不支持的,因为只是改变了位置,并没有降低难度,而且甚至更加恶心了。同时它合并了 $c_j, c_j - z_j$ 这两行,这是很好的体现,因为确实计算 $c_j - z_j$ 是一个不直观的东西,现在变得直观了。
这是例题:
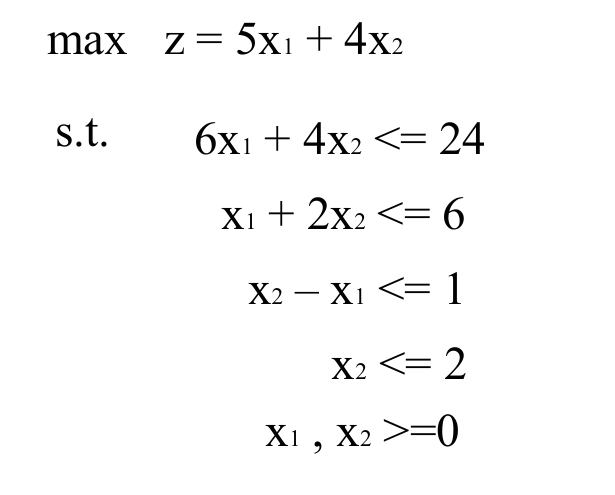
首先要将其变成标准形式,也就是下面的状态
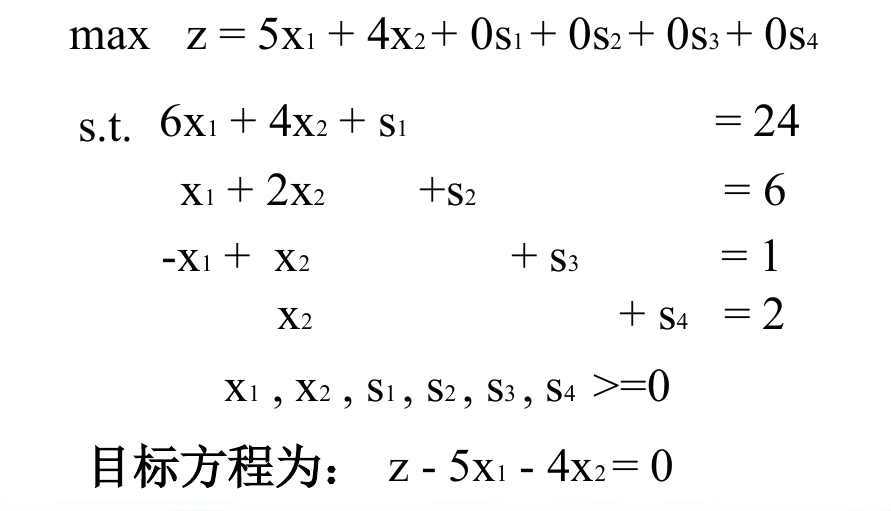
一定要让不等式组变成一组等式,所以才有了新的变量的增加,对于 $\leq$ 的式子变成具有非负右端项的等式(也就是上面的 4 个式子),引入的变量被称为“松弛变量”,如果是 $\geq$ 的式子,则称为“剩余变量”。
然后我们来做表,在做表前还是需要指出,因为有 4 个方程,所以有 4 个基变量。刚好我们对于每个方程都引入了一个松弛变量,这 4 个松弛变量刚好可以组成一组基变量(后面就会发现,不是每次都这么容易的)。
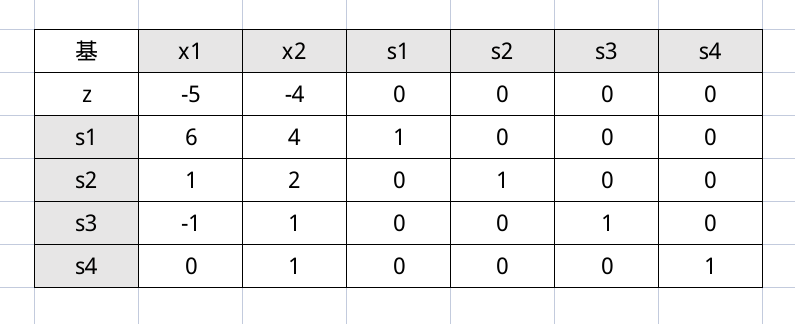
可以看到第二行填写的是目标方程的系数的相反数 $z = 5x_1 + 4x_2 + 0s_1 + 0s_2 + 0s_3 + 0s_4$ 。
然后右侧指明了基变量(还是强调,并不是每次都可以这么好运)
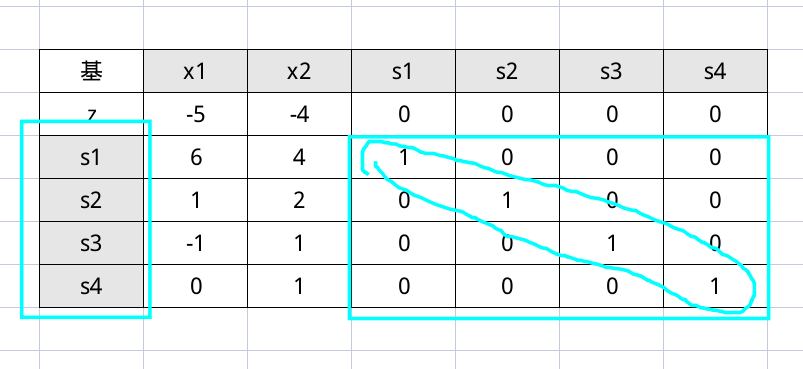
其他的系数十分显然。
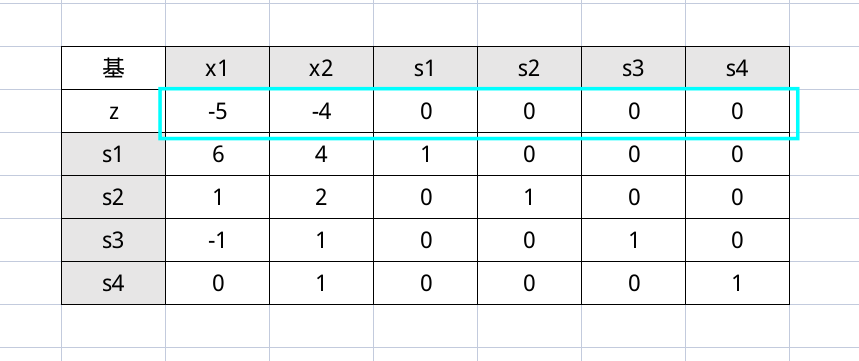
然后我们需要判断是否可以终止运算(因为单纯形法是一个迭代过程),之前是靠检验数,现在靠目标函数的系数,因为求的是最大值,所以要看系数中有没有负数(也就是实际的正数),如果有,那么说明迭代还没有结束,那么选择最小的负数(其实是选择最大的正数),作为入基变量(系数非零说明对应的变量是非基变量,很显然)。所以这次我们选择 $x_1$
选择离基变量的时候,要保证基变量都是正数,所以做如下运算
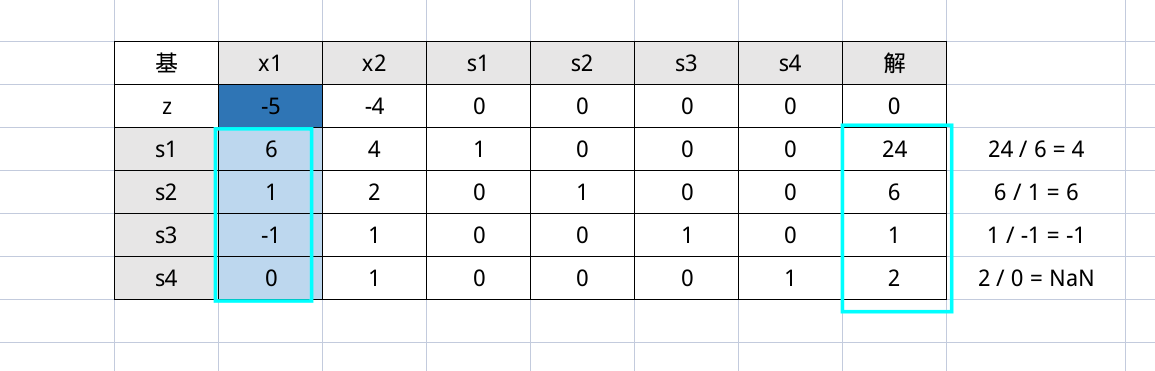
然后选择 $s_1$ 作为离基变量,因为我们只考虑最小的正数。
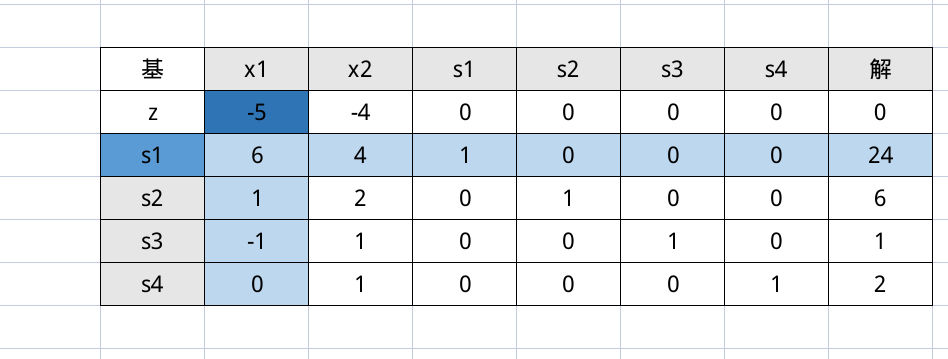
然后选择好,就可以进行无聊的行变换了,需要注意的是,第 2 行和第 8 列也是需要参与运算的,这是相比于原方法高明的地方,让形式更加统一
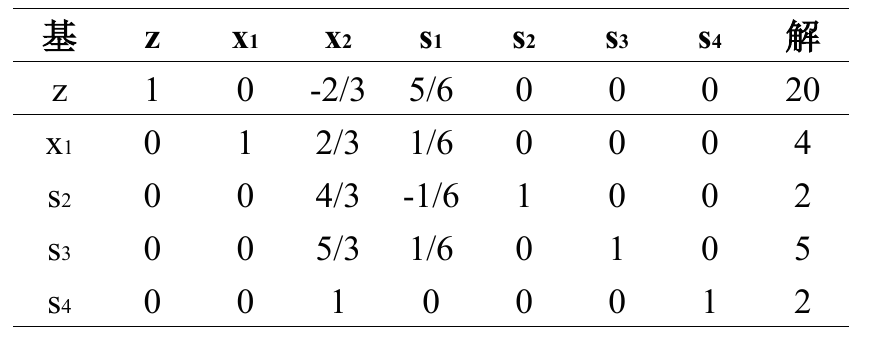
然后发现依然是可以继续进行的,因为对于 $x_2$ 依然是可以移入的,(原来判断入基变量的叫做最优性条件,判断离基变量的叫做可行性条件):
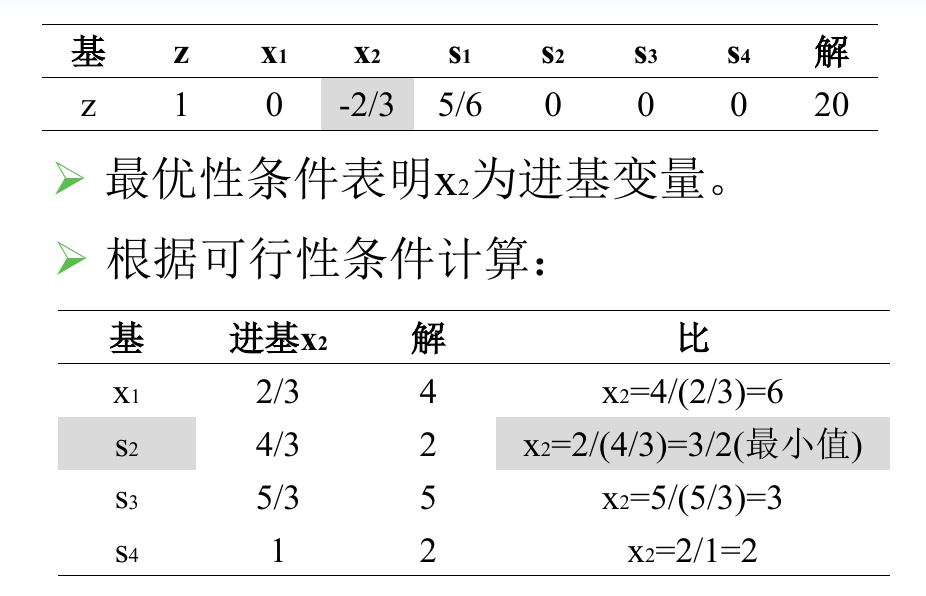
然后经过行变换,就得到了最终的结果
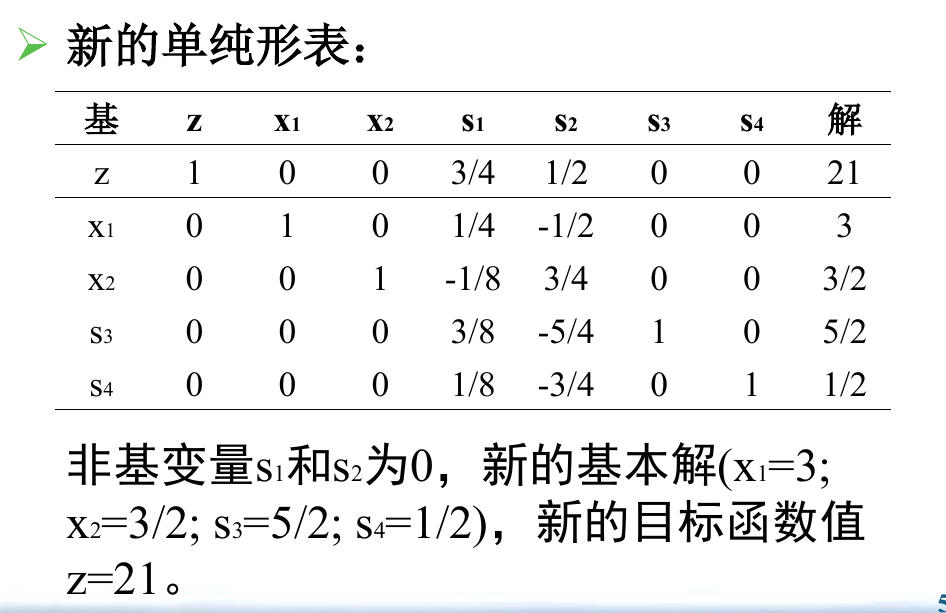
这是因为现在所有的系数都是正的了,没有办法让 $z$ 更大了。
后面课件里的第 2 列其实是多余的,去掉就好了。
最后关于判断的总结

七、大 M 法
虽然教材中叫做“改进“,但是实际上是,如果不采用下面这两种方法,就会变得没有办法实现,比如说下面的例子
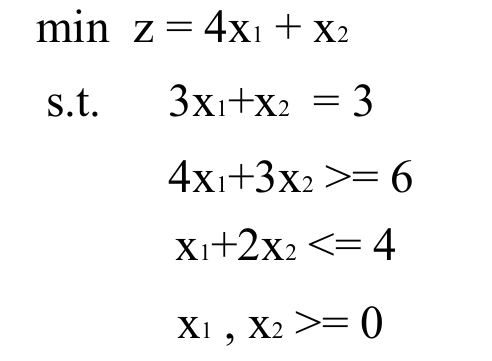
将其转换为标准形式,如下所示
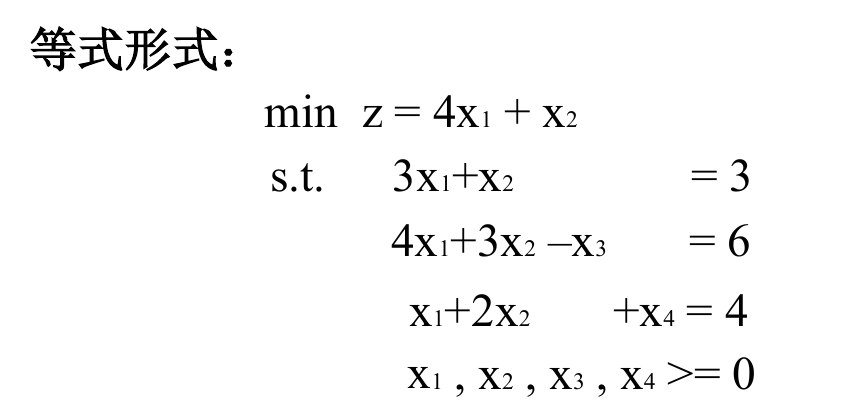
然后发现,没有初始解(就是没有显然的基变量),那么就需要再次引入变量 $R_1, R_2$,他们被称为人工变量。

但是人工变量并不是无条件加入的,我们要保证 $R_1 = 0, R_2 = 0$ 最终在最优解中成立,所以我们需要指定一个规则,其具体体现就是 M 无穷大(在最小化目标中,如果是最大化目标,就是无穷小):
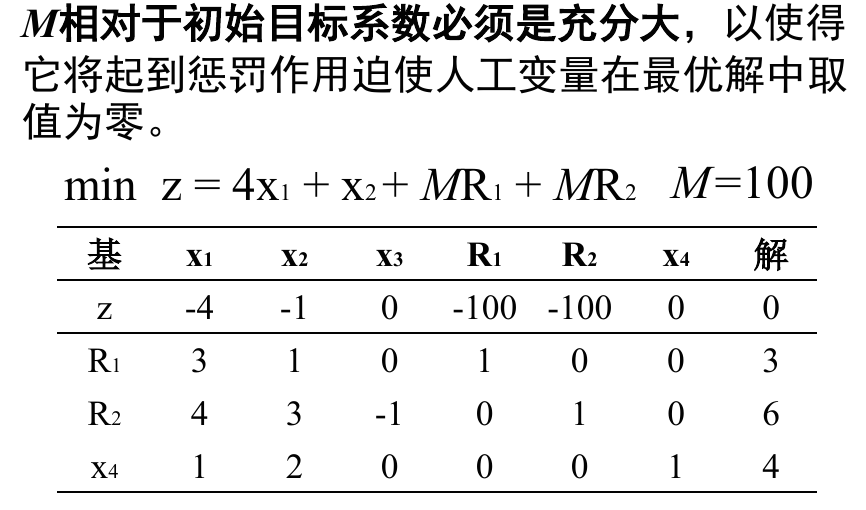
但是此时会发现这个表依然没有办法使用,因为我们需要的是在第二行,只有非基变量前有非 0 系数,现在 $R_1, R_2$ 都是基变量,但是他们前面有系数,所以利用行变换,让其为 0(利用第3,4 行)。如下所示
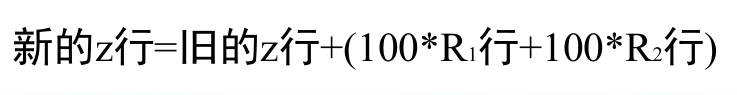
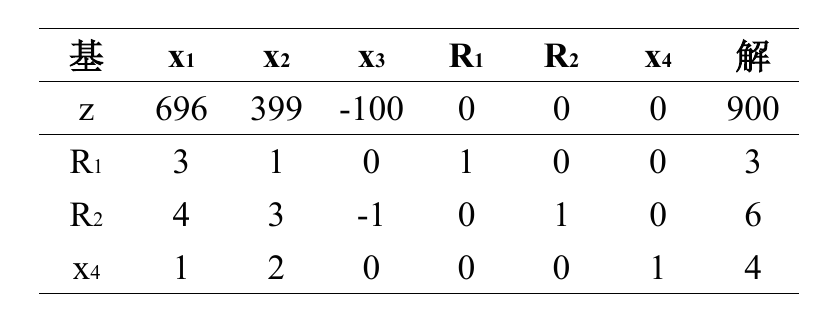
然后就可以进行正常的单纯形法。
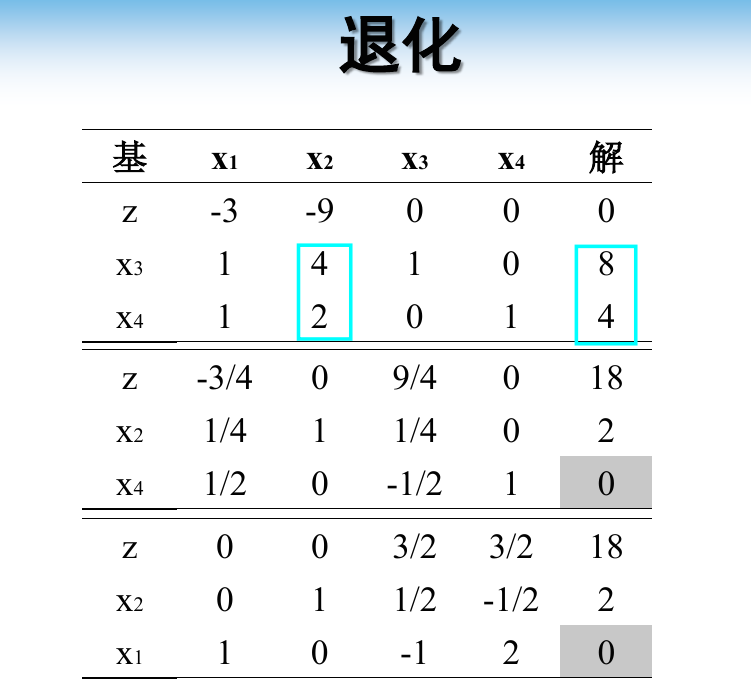
八、退化问题
退化问题最重要的是可能陷入局部最优解,也就是不是最优解的意思,所以一定要尽力避免退化。

导致退化的原因可以看做是当选择出基变量的时候,多个基变量的 $\theta$ 具有相同的值,那么无论挑选哪一个,在经过行变换后,都会导致基变量的值为 0(以后每次都会选择这个位置(这一行)作为出基变量,因此这个位置计算出的 $\theta$ 恒为 0 ),这就导致无法更新最终的目标值。如下所示