一、NumPy
1.1 参考资料
这篇文章写得实在是太好了图解链接 。
1.2 Array Matrix
这两种东西是不一样的,np.array 也可以有多维,但是它的 * 就是点对点乘法,而 @ 是点乘。但是对于 np.matrix 来说,无论是 * 还是 @ 都是点乘,sp.Matrix 同理。有如下演示
a3 = [[1, 2],
[3, 4]]
a3 = np.matrix(a3)
a4 = [[5, 6],
[7, 8]]
a4 = np.matrix(a4)
print("np.matrix")
print(a3 * a4)
print(a3 @ a4)
a3 = [[1, 2],
[3, 4]]
a3 = np.array(a3)
a4 = [[5, 6],
[7, 8]]
a4 = np.array(a4)
print("np.array")
print(a3 * a4)
print(a3 @ a4)
i, j = sp.symbols('i, j')
a3 = [[i, i],
[i, i]]
a3 = sp.Matrix(a3)
a4 = [[j, j],
[j, j]]
a4 = sp.Matrix(a4)
print("sp.Matrix")
print(a3 * a4)
print(a3 @ a4)输出为
np.matrix
[[19 22]
[43 50]]
[[19 22]
[43 50]]
np.array
[[ 5 12]
[21 32]]
[[19 22]
[43 50]]
sp.Matrix
Matrix([[2*i*j, 2*i*j], [2*i*j, 2*i*j]])
Matrix([[2*i*j, 2*i*j], [2*i*j, 2*i*j]])1.3 文件操作
genfromtxt 可以从文件(或者字符串)中读取数据,并且转化成 np.Array 类型,具体用法如下
data=np.genfromtxt("data.txt", delimiter=",", dtype=int, autostrip=True, comments="#")
print(type(data))
print(data)
print(sum(data))data.txt 如下
1, 2, 3, 4, 5 # this is a comment最终输出为
<class 'numpy.ndarray'>
[1 2 3 4 5]
15如果文件是多行的,那么就会读出一个二维的 Array 来,新的 data.txt
1, 2, 3, 4, 5 # this is a comment.
6, 7, 8, 9, 10 # this is a comment, too.
11, 12, 13, 14, 15 最终的结果是
<class 'numpy.ndarray'>
[[ 1 2 3 4 5]
[ 6 7 8 9 10]
[11 12 13 14 15]]如果想要控制读取的数据的范围,还可以
data=np.genfromtxt("data.txt", delimiter=",", dtype=int, autostrip=True, comments="#", usecols=range(4), skip_header=1, skip_footer=1)其中的参数
| 参数 | 含义 |
|---|---|
| fname | 文件名 |
| delimiter | 分隔符 |
| dtype | 数据的类型 |
| autostrip | 自动去掉空白符 |
| comments | 从指定符号后部分视为注释 |
| skip_header | 在开头跳过几行 |
| skip_footer | 在结尾跳过几行 |
| usecols | 读取的列数 |
1.4 SymPy 和 NumPy
这个问题我也没有太好的思考,只能说尽管两者十分相似,比如说都有 array 结构,但是二者是并不能显然的混用的,numpy 本质上操作的依然是 python 基础的数据类型,但是 SymPy 操作的基本对象,已经变成了它定义的对象了。
换句话说,sympy 的隔离性更好。
二、SymPy
2.1 变量
有两种方法,似乎并没有差别
x, y = sp.symbols('x, y')
k = sp.var('k')最后声明出来的 x, y, k 都是符号对象,如下所示
print(type(x))
<class 'sympy.core.symbol.Symbol'>我们可以通过在声明上加假设条件,来获得更加精确的结果,比如说
x_normal = sp.symbols('x_normal')
# 是否是符号
print(x.is_Symbol)
x_positive = sp.symbols('x_positive', positive=True)
# 是否是正数
print(x_positive.is_positive)
x_real = sp.symbols('x_real', real=True)
# 是否是实数
print(x_real.is_real)
# 是否是虚数
print(x_real.is_imaginary)
# 是否是复数
print(x_real.is_complex)
x_integer = sp.symbols('x_integer', integer=True)
# 是否是整数
print(x_integer.is_integer)另外对于变量的声明也有一些批量声明的技术
x_array = sp.symbols('x0:5')
print(x_array)
output:
(x0, x1, x2, x3, x4)2.2 常量
为了保护常量的“纯洁性”,我们可以用 sympy.S() 来声明常量,比如说
print(1 / 13) # 0.07692307692307693
print(sp.S(1) / sp.S(13)) # 1/13可以看到常量的纯洁性被很好的保护了起来。
我们可以看一下常量的类型
print(type(sp.S(1))) # <class 'sympy.core.numbers.One'>
print(type(sp.S(13))) # <class 'sympy.core.numbers.Integer'>可以看到似乎都是在 core.numbers 中的
除了可以自己设置常量,sympy 还提供了一些默认的常量
print(sp.pi) # pi
print(type(sp.pi)) # <class 'sympy.core.numbers.Pi'>0
print(sp.I) # I
print(type(sp.I)) # <class 'sympy.core.numbers.ImaginaryUnit'>
print(type(sp.oo)) # <class 'sympy.core.numbers.Infinity'>2.3 表达式
为了表示 a + b,可以使用 sp 的内置函数
a, b = sp.symbols('a, b')
print(sp.Add(a, b))当然方便的 python 肯定会重载运算符,所以一定有以下的等价写法
print(a + b)与之类似的还有 Pow, Add, Sin, Cos, Mul 之类的,能完成重载的,都完成了重载。
e = sp.Add(sp.Mul(a, b, c), sp.Pow(a, b), sp.sin(c))
print(e)最后输出为
a*b*c + a**b + sin(c)本质是和这个相同的
e_2 = a*b*c + a**b + sp.sin(c)
print(e_2)Add 不是一个方法,而是一个类(所以上面的方法其实是构造器方法),他有两个重要的属性,func 属性得到对象的类,而 args 得到其参数。使用这两个属性可以观察 SymPy 所创建的表达式
t = x - y
print(t.func)
print(t.args)输出为
<class 'sympy.core.add.Add'>
(x, -y)其实本质上说,构建的表达式就和 TensorFlow 一样,是构建了一幅表达式树。我们可以写一个函数来显示这个事情
def print_expression(e, level=0):
spaces = " " * level
if level != 0:
spaces = spaces[:-3]
spaces += "|__"
if isinstance(e, (sp.Symbol, sp.Number)):
print(spaces + str(e))
return
if len(e.args) > 0:
print(spaces + e.func.__name__)
for arg in e.args:
print_expression(arg, level + 1)
else:
print(spaces + e.func.__name__)
e_2 = a * b * c + a**b + sp.sin(c)
print_expression(e_2)可以看到输出如图
Add
|__Pow
|__a
|__b
|__Mul
|__a
|__b
|__c
|__sin
|__c似乎只要是大写开头的构造器方法,都会生成一个节点,比如说更加复杂的函数 Function
e_3 = sp.Eq(sp.Derivative(x**2+y**2, x), 7)
print(e_3)
print_expression(e_3)会输出
Equality
|__Derivative
|__Add
|__Pow
|__x
|__2
|__Pow
|__y
|__2
|__Tuple
|__x
|__1
|__7正如 tensorFlow 一样,只要不执行,这个东西绝对不会运算,但是似乎这里的运算不只有 run 这一种形式。回头细说。
2.4 自定义函数
我们可以自己定义函数,两种形式是等价的
f = sp.Function("f")
print(type(f))
g = sp.symbols("g", cls=sp.Function)
print(type(g))输出为
<class 'sympy.core.function.UndefinedFunction'>
<class 'sympy.core.function.UndefinedFunction'>与之形成对比的是
print(type(sp.Derivative(x**2 + y**2, x)))输出为
<class 'sympy.core.function.Derivative'>请注意 Function 虽然是一个类,但是上面的语句所得到的 f 并不是 Function 类的实例。和预定义的数学函数一样,f 是一个类,它从 Function 类继承。只有指定了具体的参数(本质是将 f 做为一个构造器),才可以实例化出这样的函数,如下所示:
t = f(x, y)
print(type(t)) # f
print(t.func) # f
print(t.args) # (x, y)有一个很有意思的事情,就是自定义函数并没有我们常以为的“表示某种特定的符号和运算符的组合”的效果,因为这个定义其实是
sp.Derivative(x**2 + y**2, x)就可以完成的。所以 f(x, y) 就真的只是 f(x, y) ,我们并不知道里面是啥内容,而且永远不知道,它就真的只是一个函数符号的意思。
所以我们一般用它来实现函数本身的求解(不是求解某个变量)。比如求解数列的通项公式,微分方程的求解。
2.5 关系
最近只用到了 Eq 来构造方程,里面似乎包括很多种,比如说 Less 啥的
print(type(e_3)) # <class 'sympy.core.relational.Equality'>在 SymPy 中,表达式可以直接表示值为 0 的方程,这使得后面的各种操作会更加灵活。
2.6 矩阵
矩阵的声明方法与 numpy 中的类似
A = sp.Matrix([[x, a], [b, y]])
print(A)
print(A.is_Matrix)
print(type(A))输出为
Matrix([[x, a], [b, y]])
True
<class 'sympy.matrices.dense.MutableDenseMatrix'>并且和 numpy 一样,都重载了运算符
print(A * 3)
print(type(A * 3))
print(A @ B)
print(type(A @ B))
print(A.T)
print(A**2)
print(type(A**2))输出为
Matrix([[3*x, 3*a], [3*b, 3*y]])
<class 'sympy.matrices.dense.MutableDenseMatrix'>
Matrix([[2*a + x], [b + 2*y]])
<class 'sympy.matrices.dense.MutableDenseMatrix'>
Matrix([[x, b], [a, y]])
Matrix([[a*b + x**2, a*x + a*y], [b*x + b*y, a*b + y**2]])
<class 'sympy.matrices.dense.MutableDenseMatrix'>可以看到,不再有表达式树的结构了。希望表达式树,似乎应该求助 TensorFlow 。
2.7 操作
运算一般都是对于表达式对象或者方程对象进行操作。
2.7.1 变形
化简
simplify((x+2)**2 - (x+1)**2)展开
expand(log(x*y**2))替换
# 待定系数法
xn = c1 * lams[0]**n + c2 * lams[1]**n
x0 = xn.subs(n, 0)
x1 = xn.subs(n, 1)可以利用 subs 将某个表达式换成一个新的表达式(不一定非得是常量)。
级数展开
print((1/cos(x)).series(x, 0, 10))输出
1 + x**2/2 + 5*x**4/24 + 61*x**6/720 + 277*x**8/8064 + O(x**10)2.7.2 求解
solve 可以求解普通方程
solve(a*x**2+b*x+c, x)也可以求解方程组,后面需要依次写定要求解的变量,比如这里的 x, y
solve ((x**2+x*y+1, y ** 2+x*y+2 ), x, y )dsolve 用于微分方程的求解
dsolve(Derivative(f(x),x) - f(x), f(x))rsolve 用于递归表达式的求解(可以用于解差分方程),相对于需要给出带求解的通项表达式,还需要给出初始值。
# 声明变量
n = sp.var('n')
# 声明递归表达式
x = sp.Function('x')
f = 2 * x(n + 2) - x(n + 1) - 2 * x(n)
# 调库求解
xn = sp.rsolve(f, x(n), {x(0): -2, x(1): 0})2.7.3 微积分
微积分都用两种方式,因为微分和积分都是有固定的 Function 去描述的,所以可以直接求值表达式树,如下
t = Derivative(sin(x), x) # 创建了一个导函数对象,表达式后面的参数是对谁求导
print(t.doit()) # 类似于 tensorflow 中的 session.run当然也可以直接用 diff ,并且更加直观
diff(sin(2*x), x) # 不太面向对象
sin(2*x).diff(x) # 比较面向对象对于多个变量求高阶导数,可以有如下形式
print(diff(sin(x * y), x, 2, y, 3)) # 对 x 求二阶导且对 y 求三阶导数利用 Integral 进行不定积分
e = Integral(x*sin(x), x)
e.doit()进行定积分
e2 = Integral(sin(x)/x, (x, 0, 1))
e2.doit()
e2.evalf()不过 SymPy 本质是符号运算系统,而定积分本质是数值运算,所以很有可能运算不出来。
对于多重定积分,格式如下
integrate(f, (x, a, b), (y, c, d))对应的表达式如下
2.7.4 求极限
limit(sin(x)/x, x, 0)
limit(sin(x)/x, x, oo)三、SciPy
3.1 线性规划
首先谈一下对于线性规划的理解
本质上,最终的求解结果 $z$ ,可以看做是一个涉及 $c, A, b$ 的隐函数,再加上边界条件,我们就可以完成求解,而实际也是这样的,scipy 中的 linprog 就是这样,只需要输入这些东西,就可以获得一个最大值 $z$ 的结果。其函数签名(简化版)如下
linprog(c, A_ub, b_ub, A_eq, b_eq, bounds)多说无益,举个复杂的例子
其求解代码如下
import scipy as sp
import numpy as np
c = np.array([2, 3, -5]) # 目标方程系数矩阵,因为默认 max,所以这里要取相反数
A_eq = np.array([[1, 1, 1]]) # 等式系数矩阵
b_eq = np.array([7]) # 等式增广部分
A_ub = np.array([[-2, 5, -1], [1, 3, 1]]) # 上界(upper bound)系数矩阵,所以第 1 行要取反
b_ub = np.array([-10, 12]) # 上界增广部分
bounds = [(0, 7), (0, 7), (0, 7)] # 约束条件,每个的范围都是 0 ~ 7
# 求解
result = sp.optimize.linprog(-c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds)
print('最优解为:', result.x)
print('最优值为:', result.fun)输出如下
最优解为: [6.42857143 0.57142857 0. ]
最优值为: -14.5714285714285733.2 拟合
scipy 有内置的拟合函数,大致写法如下
scipy.optimize.curve_fit(f, xdata, ydata, p0, maxfev)其参数有:
f:拟合函数的形式,是一个函数,其函数参数就是我们拟合的时候需要的东西xdata:自变量数据ydata:因变量数据p0:起始数据(给出的是f的参数),可以不指定,指定后有可能会使迭代变快,不过更多的用于规范参数的格式(f有可能含有变长参数)maxfev:最大拟合次数
其返回值为
# 返回值
popt: 数组,参数的最佳值,以使的平方残差之和最小。f(xdata, *popt) - ydata
pcov: 二维阵列,popt的估计协方差。对角线提供参数估计的方差。可以看出,我们最想要的是 popt ,对于 pcov 课程不太涉及。
常见例子为
def my_func1(x, w1, a1, b1, w2, a2, b2):
return w1 * Gauss(x, a1, b1) + w2 * Gauss(x, a2, b2)
popt = optimize.curve_fit(my_func1, x_train, y_train, maxfev=500000)[0] # 因为不需要 pcov,所以只要第一个返回值四、CvxPy
4.1 更加自然
cvxpy 是在学线性规划的时候介绍的,在我的理解中,线性规划问题可以用 SciPy 库去求解,cvxpy 似乎是为了让线性规划的描述更加自然而开发的包,比如说在 3.1 具的例子,如果用 cvxpy 来写的话,可以写成这样
x = cp.Variable(3, pos=True) # 声明变量
obj = cp.Minimize(-2 * x[0] - 3 * x[1] + 5 * x[2]) # 声明目标函数
cons = [ # 声明约束条件
x[0] + x[1] + x[2] == 7,
2 * x[0] - 5 * x[1] + x[2] >= 10,
x[0] + 3 * x[1] + x[2] <= 12,
]
prob=cp.Problem(obj, cons)
prob.solve() # 求解
print("最优值为:", prob.value)
print("最优解为:", x.value)
print(type(x))
print(type(obj))
print(type(cons))最后输出为
最优值为: -14.571428570710513
最优解为: [6.42857143 0.57142857 0. ]
<class 'cvxpy.expressions.variable.Variable'>
<class 'cvxpy.problems.objective.Minimize'>
<class 'list'>4.2 凸优化
cvxpy 本质上是一个凸优化库,所以不是凸优化的问题是没有办法用这个库来求解的。
五、Matplotlib
5.1 架构
如图所示
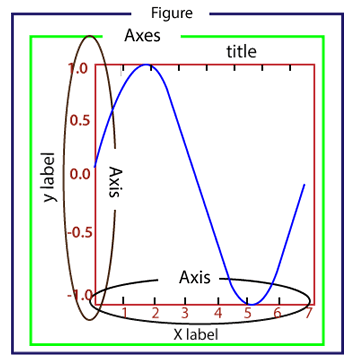
但是似乎学不学的吧,因为这种比较普世和灵活,如果只是为了应付简单的画图任务,完全不需要这种复杂的结构,其比较规范的结构如下所示
import matplotlib.pyplot as plt
import numpy as np
# 绘图数据
x = np.arange(0, np.pi*2, 0.05)
y = np.sin(x)
# 首先创建画布
fig = plt.figure()
# 添加两个轴区域(也就是有坐标轴的区域)
axes1 = fig.add_axes([0.1, 0.1, 0.8, 0.8]) # main axes
axes2 = fig.add_axes([0.55, 0.55, 0.3, 0.3]) # inset axes
# 在两个区域上分别绘图
axes1.plot(x, y, 'b')
axes2.plot(x,np.cos(x),'r')
# 为轴区域设置一些标签
axes1.set_title('sine')
axes2.set_title("cosine")
# 展示
plt.show()其效果如下,可以看到很灵活
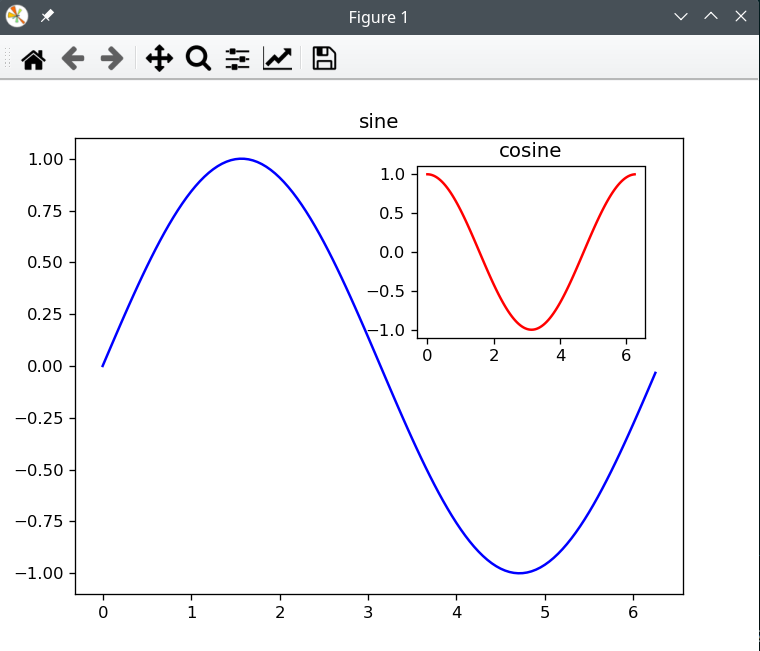
另外我们一般只用 pyplot,虽然我不知道为啥,但是写成这样就可以了
from matplotlib import pyplot as plt5.2 基本操作
首先说,下面的代码似乎并不规整,规整的代码是先创建一个 figure 然后再其上创建 Axes 然后再干一大堆事情,但是我懒了,所以就选了一些比较简单的方法。可以说,上面的写法是面向对象的,而下面的写法是面向过程的。
5.2.1 画一个图
from matplotlib import pyplot as plt
import numpy as np
# 制造 x, y 数据
x = np.arange(0, np.pi * 2, 0.05)
y = np.sin(x)
# 绘图
plt.plot(x,y)
# 绘制一些标签
plt.xlabel("angle")
plt.ylabel("sine")
plt.title('sine wave')
#使用show展示图像
plt.show()5.2.2 在一张图上画两个曲线
from matplotlib import pyplot as plt
import numpy as np
# 制造 x, y 数据
x = np.arange(0, np.pi * 2, 0.05)
y1 = np.sin(x)
y2 = np.cos(x)
# 绘图
plt.plot(x, y1, 'b-') # 'b-' 指定了颜色是 blue,线条是直线
plt.plot(x, y2, 'r*') # 'r*' 指定了颜色是 red,线条是 * 号
# 绘制一些标签
plt.xlabel("angle")
plt.ylabel("sine")
plt.title('sine wave')
#使用show展示图像
plt.show()5.2.3 在一个画布上画多张图
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0.1, 100)
# 作图 1,意思是在一个 2 x 2 的格子里,挑选第 1 个位置,也就是 (1, 1) 位置
plt.subplot(2,2,1) # 等效于 plt.subplot(221)
# 此时的绘图就会绘制在 (1, 1) 里了
plt.plot(x, x)
# 作图 2,此时再次使用,以后的图就会绘制在 (1, 2) 上了
plt.subplot(2, 2, 2)
plt.plot(x, -x)
# 作图 3
plt.subplot(2, 2, 3)
plt.plot(x, x**2)
# 这里给出了一种对于线条样式的规范写法,好吧,是格子的规范写法,alpha 应该是透明度
plt.grid(color='r', linestyle='--', linewidth=1, alpha=0.3)
# 作图 4
plt.subplot(224) # 这里给出了简写写法
plt.plot(x, np.log(x))
# 展示
plt.show()其效果如下:
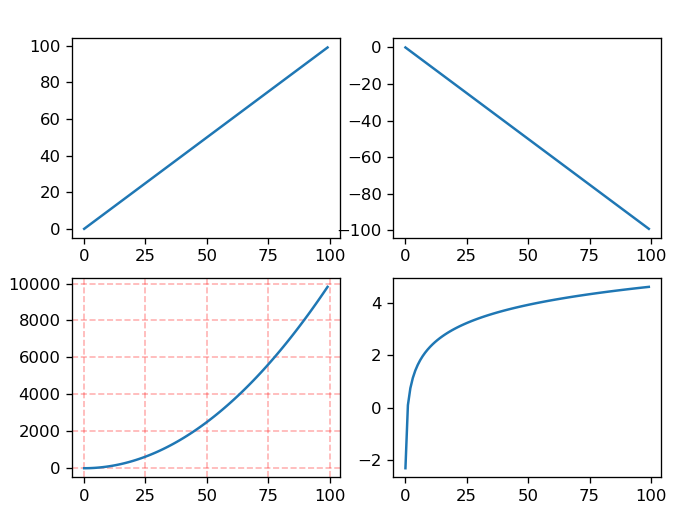
5.2.4 多种不一样的图
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.family']='sans-serif'
#解决负号'-'显示为方块的问题
matplotlib.rcParams['axes.unicode_minus'] = False
x = np.arange(0.1, 10)
plt.subplot(3, 2, 1) # 等效于 plt.subplot(221)
# 此时的绘图就会绘制在 (1, 1) 里了
plt.stackplot(x, x)
plt.subplot(3, 2, 2)
plt.bar(x, x)
# 作图 3
plt.subplot(3, 2, 3)
plt.stem(x, x**2) # 火柴图
# 作图 4
plt.subplot(324)
plt.scatter(x, np.log(x)) # 散点图
# 作图 5
plt.subplot(325)
labels=['第一季度', '第二季度', '第三季度', '第四季度'] # 饼的标签
data=[23, 45, 50, 40] # 饼的份额
explodes=[0.1,0.1,0.1,0.1] # 让各角饼之间留有一定的空隙
# 饼状图
plt.pie(x=data,labels=labels,explode=explodes,autopct="%0.1f%%",shadow=True)
plt.savefig("plt.png")
plt.show()效果如下:
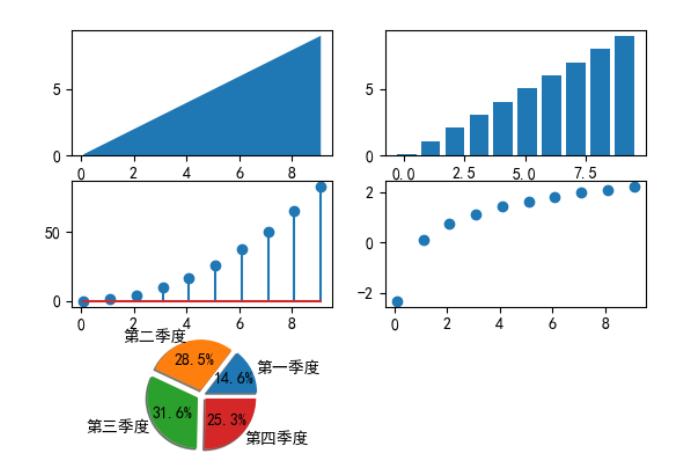
5.2.5 保存图像
plt.savefig("plt.png")
# savefig 一定要在 plt.show 之前,似乎 plt.show() 会清空画像
plt.show()5.2.6 图例
可以通过在绘图的时候增加 label 参数,然后用 plt.lengend(1) 来解决
import matplotlib.pyplot as plt
import numpy as np
import math
x1 = np.arange(0,5.1,0.01)
x1 = math.pi*x1
y1 = np.sin(x1)
y2 = np.cos(x1)
#在绘制图像时定义每条函数图像的label值,用于显示在图例上
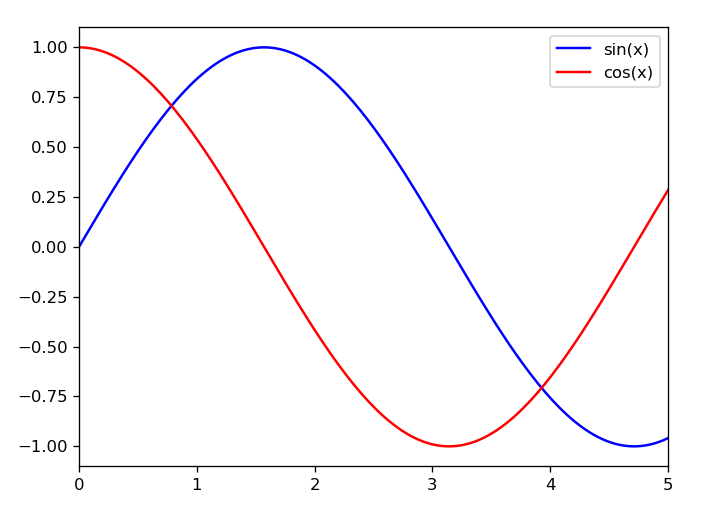
p1 = plt.plot(x1,y1,label='sin(x)',color='b')
p2 = plt.plot(x1,y2,label='cos(x)',color='r')
plt.xlim(0,5)
#绘制图例,loc表示图例位置,1代表右上方
plt.legend(loc=1)
plt.show()效果
5.3 解决乱码问题
按照如下操作即可在 win 下解决问题
import matplotlib
import matplotlib.pyplot as plt
# 解决中文乱码问题
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.family']='sans-serif'
#解决负号'-'显示为方块的问题
matplotlib.rcParams['axes.unicode_minus'] = False 但是如果是 manjaro 需要拷贝字体:
- 将 windwos 中
fonts目录下的 simhei.ttf 拷贝到/.../lib/python2.7/site-packages/matplotlib/mpl-data/fonts/ttf(文件路径根据实际情况修改)目录中。 - 删除
~/.cache/matplotlib的缓冲目录