钟鼓楼

钟楼瘦，鼓楼胖

0%

海边拾贝-FuseMax

Posted on Edited on In
Symbols count in article: 5.1k Reading time ≈ 5 mins.

这篇工作比较缝合，它引用了 3 个 idea：

TeAAL 提出用 Einsum 的形式去描述算子，并指导加速器的设计。但是 Einsum 只能描述仅包含加法和乘法的算子，对于 Flash-Attension 这种包含指数运算（softmax）和迭代运算的算子无法描述，于是作者借用了 Extended Einsum 的形式描述了 Flash Attension 算子并实现了 FuseMax 加速器，同时论证了 pass 抽象的合理性。

而实际上，TeAAL 提出的用 Einsum 指导加速器设计的思路并没有因为使用了 Extended Einsum 而被拓展；FuseMax 所展现的性能优势，大部分来自于 Flash-Attension 算法本身，而不是其硬件实现。

一、Background

1.1 Flash Attention, Pass

Flash-Attention 是一种 Attention 算子的实现，相比于传统的实现，它可以降低内存带宽的需求，并且使用更少的片上内存，更适合当前加速器存在的 memory bound。为了达到这个目的，我们需要：

  • 尽可能少的从内存中读取数据 -> 算法设计的 pass 数要少
  • 尽可能少使用片上内存 -> tile 后 reduce

而这两个需求都被 softmax 的传统实现阻止了，softmax 的表达式如下：

img

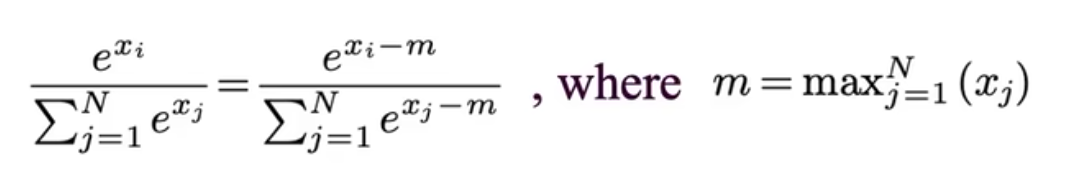
传统的 softmax 实现是一种 3-pass 的实现：

img

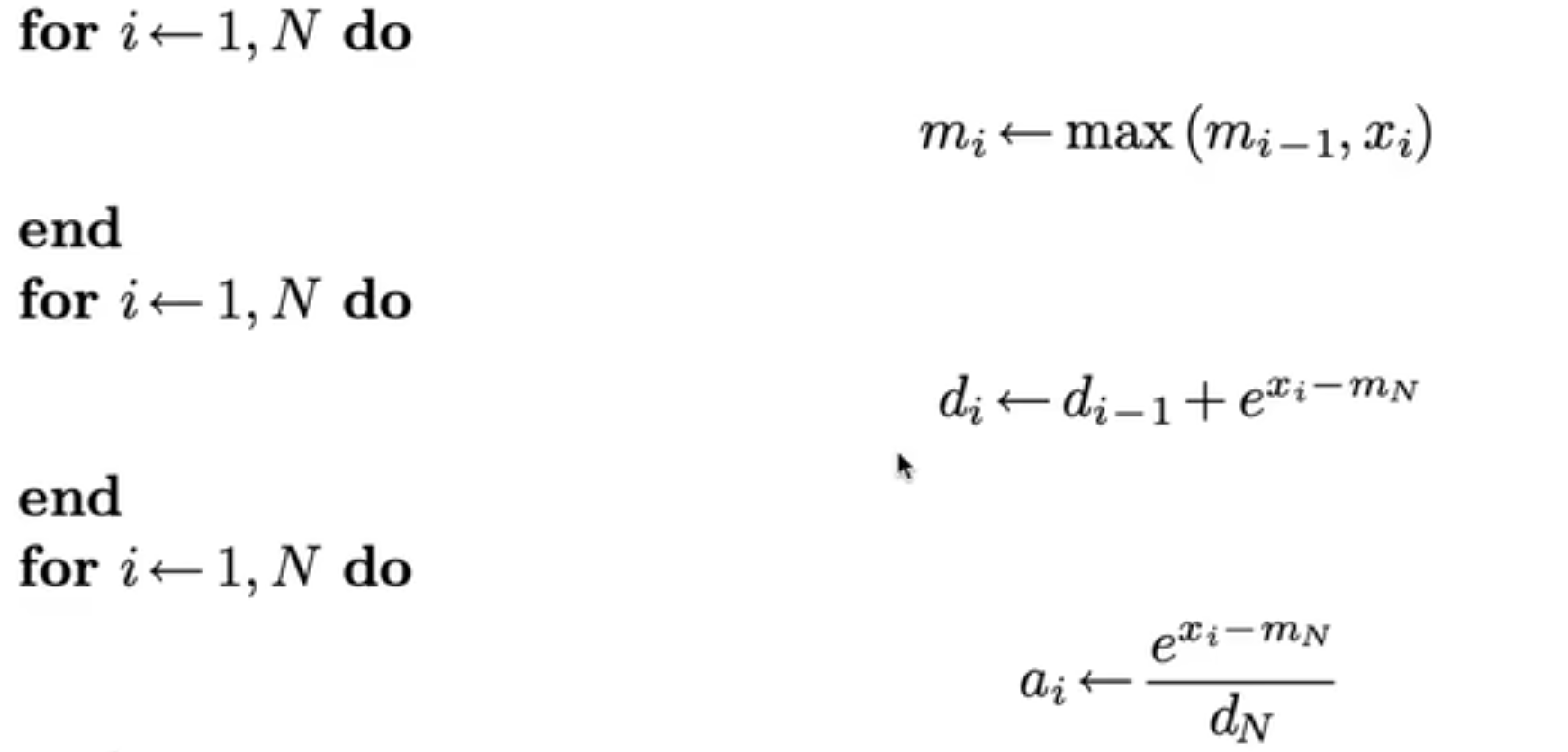
所谓的 pass，就是需要访问输入的次数：

the number of times a given element of an input must be revisited after visiting every other element of the input.

因为 softmax 需要先遍历所有元素计算出 max 值，然后根据 max 值遍历所有元素计算分母，再根据分母计算分子。

在 flash-attention 之前，有 2018 online-softmax 工作，将算法优化成了 2-pass 的。他将第 1，2 轮进行了合并：

img

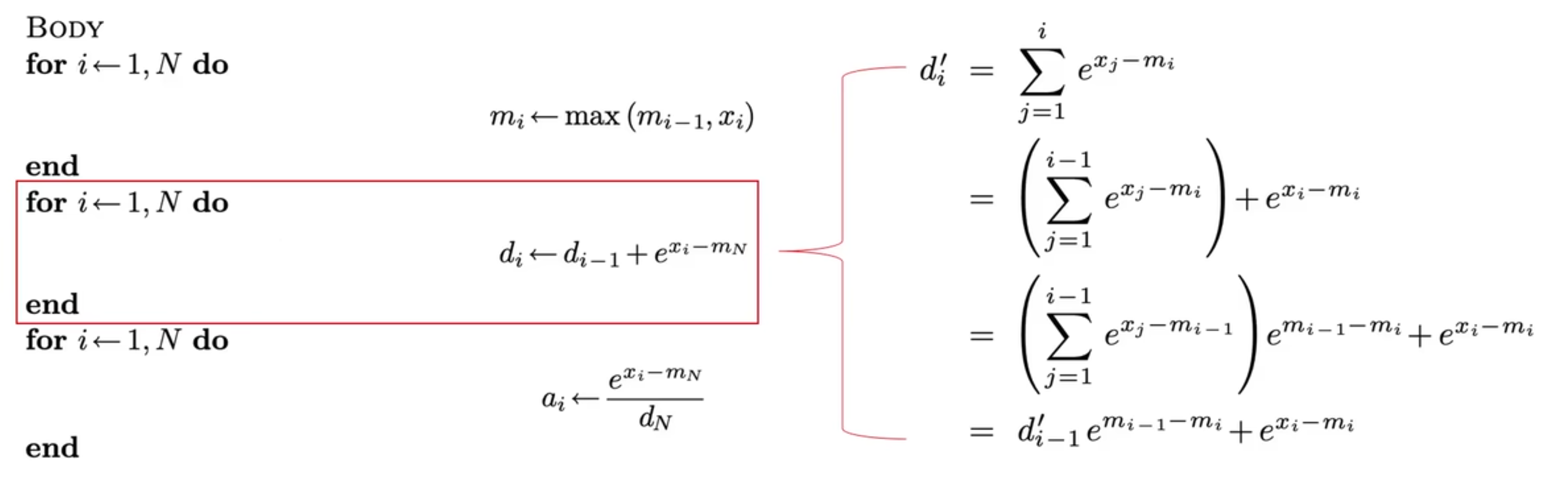
最终结果如图：

img

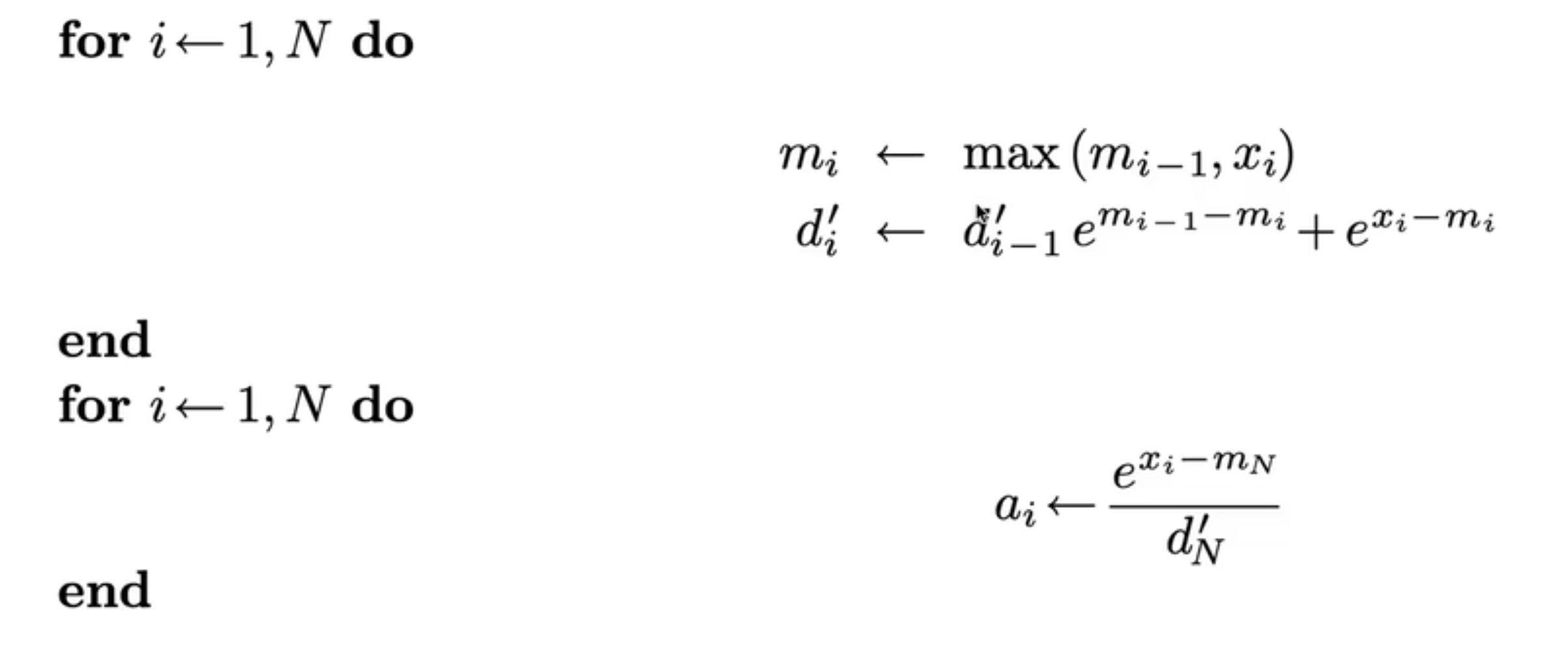
如果仅在 softmax 层，那么 2-pass 就是极限了，不过如果考虑整个 Attention，那么是可以继续优化成 1-pass 的算法，这就是 Flash-Attention，2-pass 的 Attention 表示如下：

img

然后我们注意到（直观上说，是利用了 a 这个数组并不是最终结果，而是会被 reduce 的性质）：

img

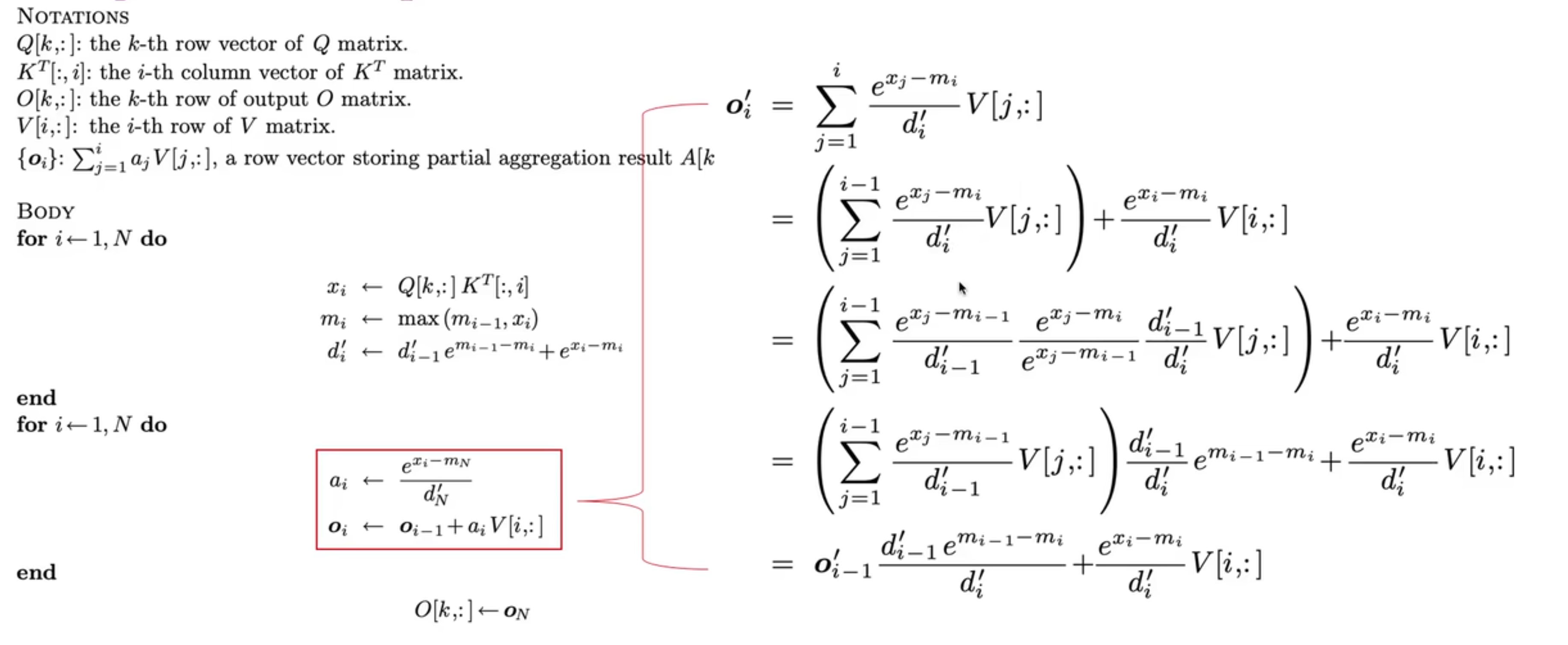
整理后得到：

img

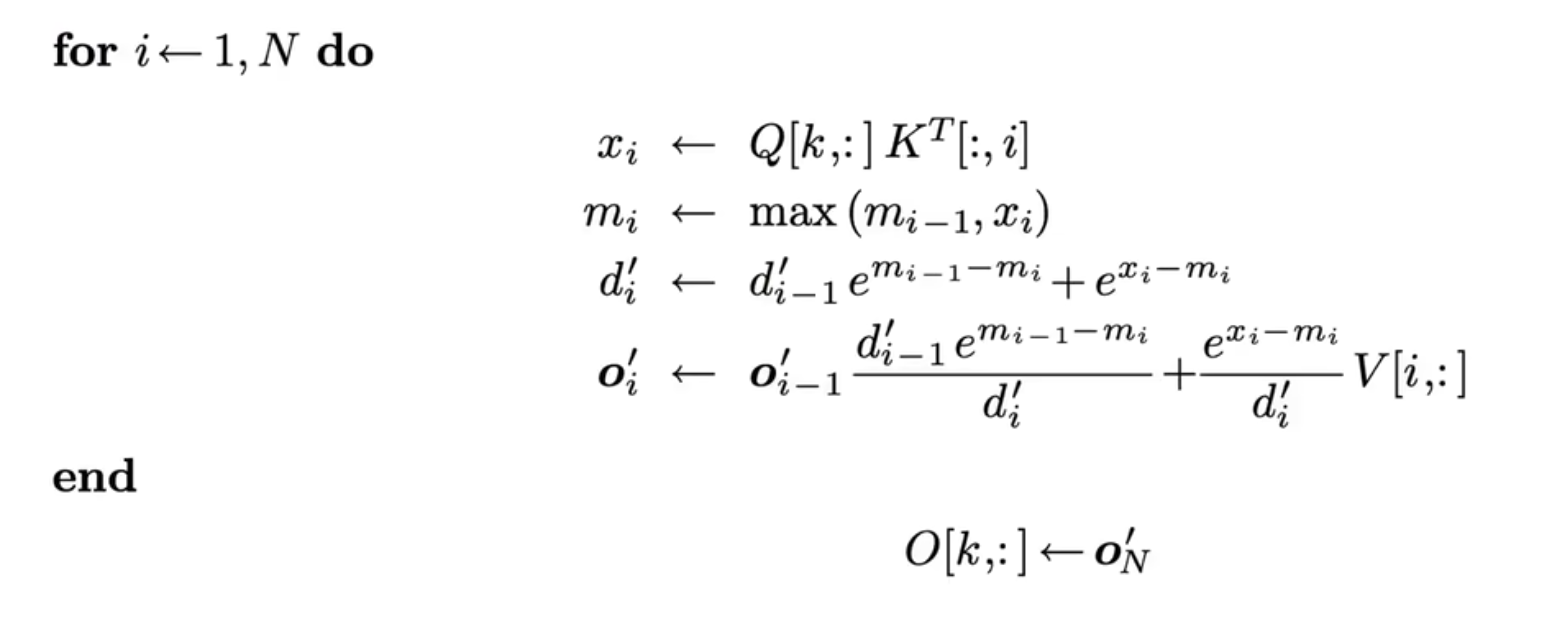
这就是一个 1-pass 的 Flash-Attention 算法。在此基础上，如果增加了 tile 操作，那么就会获得完全体的 Flash-Attention，但这本文的重点是对于 pass 的优化。

img

1.2 Einsum Notation

爱因斯坦求和标记（Einstein summation notation）是一种标记的约定，用于描述张量运算。比如说二维矩阵乘法就可以被描述为：

img

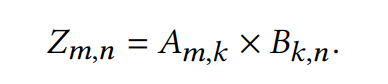
而矩阵与向量的乘法可以被描述为：

img

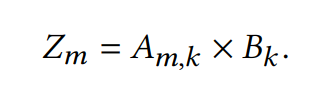
Einsum 的输入包括张量，如和其对应的坐标，如和，还有输出矩阵对应的坐标，如，比如在 numpy 中，$$$$和$$$$的矩阵乘法写作：

np.einsum('mk,kn->mn', A, B)

Einsum 的特点在于，它将 compute 和 reduce 阶段完全区分开了，而不是混在一起，更加清晰了。

具体而言，在 compute 阶段，我们会根据输入坐标，构建一个迭代空间，然后遍历空间中的每一个点进行计算，得到一个相同维度的张量。以矩阵乘法为例，输入坐标是和，我们构建的迭代空间是。经过计算得到的张量是。

在 reduce 阶段，我们需要将我们得到的张量 $z{m,k,n}$ 与输出坐标 进行比对，发现多了一个 维度。所以我们会沿着多出的维度进行规约，然后就可以得到 $$z{m,n}=[\sum^{K}{k=1}[a{m,k} \times b_{k,n}]$$。

对比我平时用的矩阵乘法，可以看到 compute 和 reduce 是混合在一起的。

 for (int i = 0; i < M; i++) {
     for (int j = 0; j < N; j++) {
        for (int k = 0; k < K; k++) {
            Z[i][j] += A[i][k] * B[k][j];
         }
    }
}

1.3 TeAAL

TeAAL 是一个加速器模型 generator，可以根据不同算子生成不同的加速器模型。在它的设计中，算子需要使用 Einsum Cascade 来进行描述，也就是一系列的 Einsum 。

使用 Einsum 好处在于，引入了迭代空间，使得许多加速器设计中的优化和 tradeoff 都非常清晰。TeAAL 提出了 3 个维度的优化：

  • Loop Order：迭代空间“是还是”？这会影响数据是 stationary 的，还是 stream 的。
  • Splitting：运算中我们常常将输入分块计算，也可以视为在对迭代空间分块。
  • Work scheduling：根据迭代空间计算出的张量，是如何摆放的？包括空间和时间维度。

总之 Einsum 是一个非常适合数学化表述加速器设计的标记。

1.4 Extended Einsum

传统的 Einsum 是不能指定运算符的，比如说在 Numpy 中，Compute 阶段只能使用乘法，Reduce 阶段只能是加法：

np.einsum('mk,kn->mn', A, B)

而 Extended Einsum 则允许自定义 Compute 和 Reduce 阶段的运算符，例如：

img

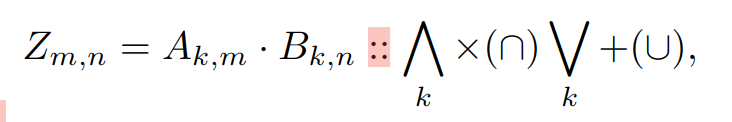
是 Compute 阶段使用的运算符，是 Reduce 阶段使用的运算符。

除此之外，Extended Einsum 还可以表达循环，比如说前缀和计算：

img

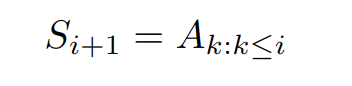
还可以表达递推式，同样是前缀和计算：

img

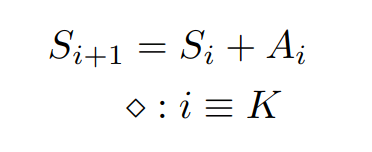
有了 Extended Einsum，我们就可以描述 Flash-Attention 这种包含许多复杂运算和递推式的算法。

二、Contribution

2.1 Einsum 与 Pass

本文认为，如果将算子写成 Einsum 的形式，那么是有助于确定算子的 Pass 数的，比如说这个算子，就是 2-Pass：

img

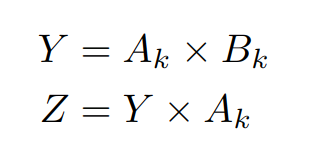
而相同功能的另一个算子，就是 1-Pass：

img

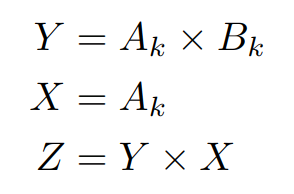
本文认为，迭代空间也可以被表示成一个 fibertree，而根据这些 fibertree 就可以判断 pass。首先，我不知道为什么原本适用于稀疏矩阵表示的 fibertree 要用来表示一个非常稠密的迭代空间（它可能是想说 fibertree 用于表示根据迭代空间生成的那个向量），其次，我不知道为什么表示成了 fibertree，就可以看出来是多少个 Pass。

它原文中对迭代空间的 fibertree 定义如下，非常的简略：

The is-fibertree is a special tree where each fiber belongs to a rank in the iteration space of the Einsum.

而他介绍的根据 fibertree 识别 Pass 的方法，则依赖于非常主观的“Dependency”，其定义基本上和 Flash-Attention 中的定义一样：

Now, in a scenario where fibers for a particular rank exist in multiple is-fibertrees; in each, they project to the same tensor; and there is a dependency such that all of the elements of the earlier is-fibertree’s fiber must be read before any element can be read again by the later is-fibertree (for all mappings of the cascade**)**, we refer to that read-read sequence as creating an additional pass.

这种冗余和主观定义的方式，指示它无法编写成一个程序来自动优化 Pass 数目：

We leave a full analysis of the space of pass-reduction approaches to future work.

2.2 用 Einsum 表示 Flash-Attention

用 Extended Einsum 表示 Flash-Attention，结果如图：

img

文章只是将 Flash-Attention 换了一种标记形式（从伪代码到 Einsum Cascade），其算法的实质并没有发生改变。

2.3 将 Flash-Attention Map 到硬件上

本文将 Flash-Attention 实现到了 Timeloop and Accelergy 模拟的 spatial 架构上：

img

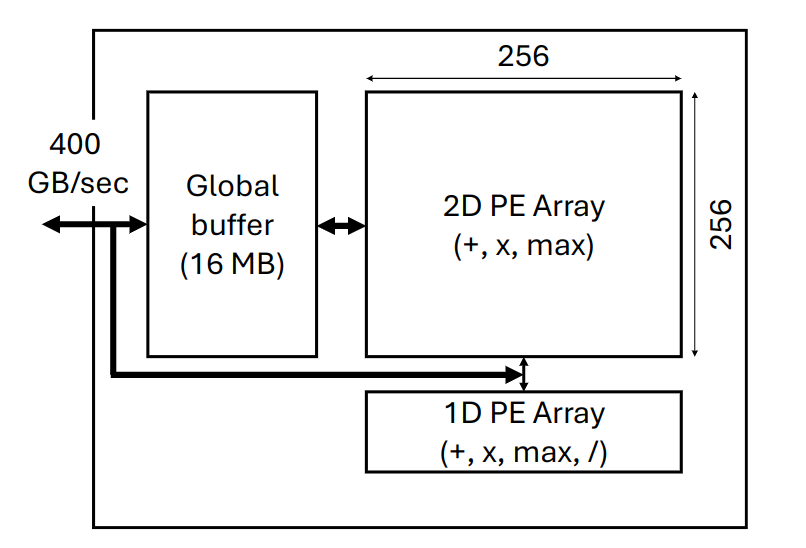
传统的 Attention 加速器，使用 2D Array 来计算矩阵乘法，使用 1D Array 来计算 softmax，这种安排的缺点在于，1D Array 计算 softmax 非常吃力，进而导致 2D Array 需要等待 1D Array 的计算，造成了低计算利用率。

但是 Flash-Attention 算法本身就融合 softmax 到前面的计算中，所以有一部分的 softmax 的计算任务，是可以放到 2D Array 中计算的，这样两个部分的计算任务就更加均衡了。

此外，2D Array 的 fill 和 drain 的开销很大，所以需要使用流水线的方法摊还（amortize）开销。

三、Evaluation

3.1 Setup

实验在 TimeLoop 模拟器上进行（全是 Python 代码），BaseLine 分别是一个未经优化的 Attention 加速器，和 FLAT（经过 Fusion 等优化，但是依然使用普通 Attention 算法的加速器）。

WorkLoad 有 BERT，TrXL，T5，XLM。

3.2 Compute Utilization

在真实负载情况下，计算单元利用率的比值：

img

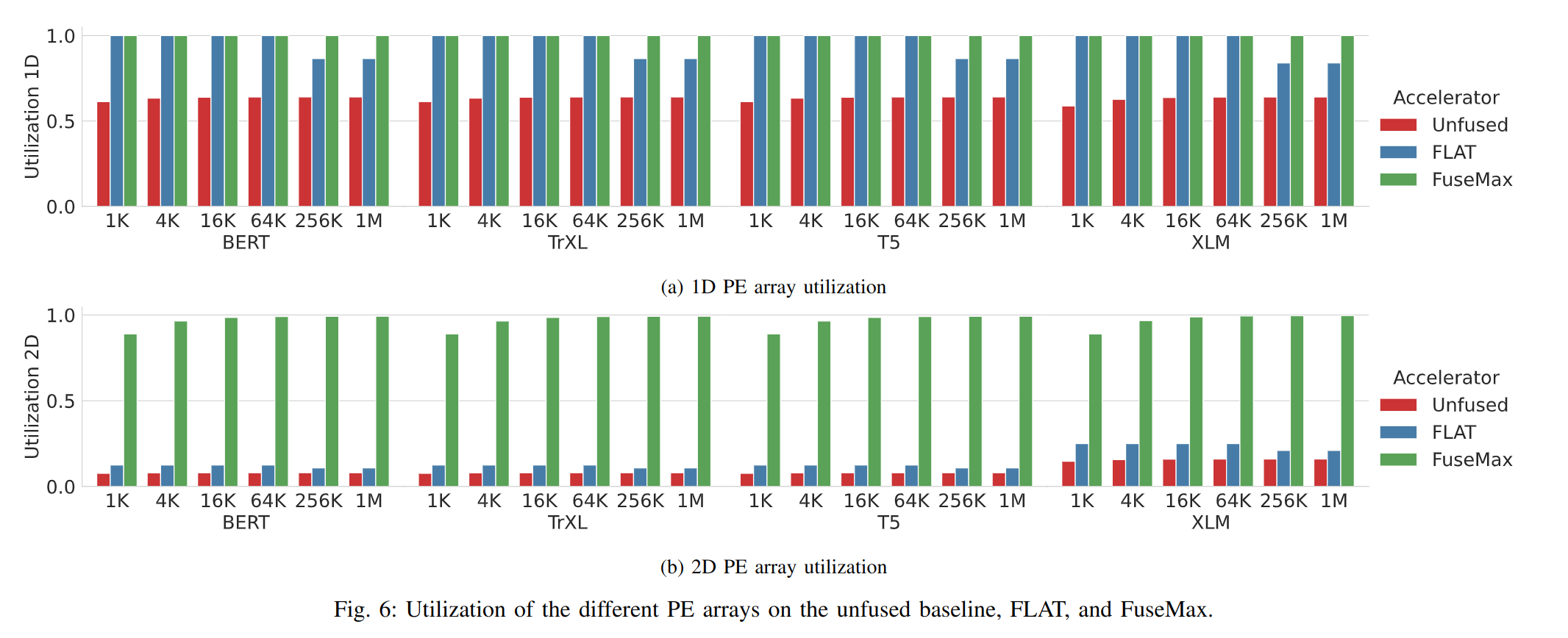
正如前文分析的，Baseline 的 2D Array 受到 1D Array 的拖累，导致利用率极低。

而在序列长度过长时，传统 Attention 算法会导致 global buffer 溢出，进而计算率下降，而 Flash-Attention 则没有这个问题。

3.3 SpeedUp

在 attention 时的加速比：

img

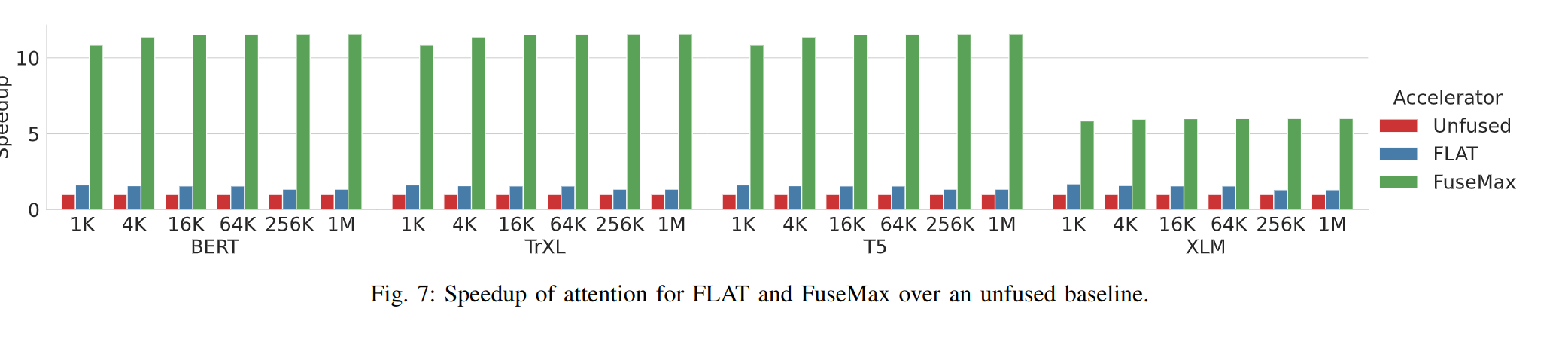
在 inference 时的加速比：

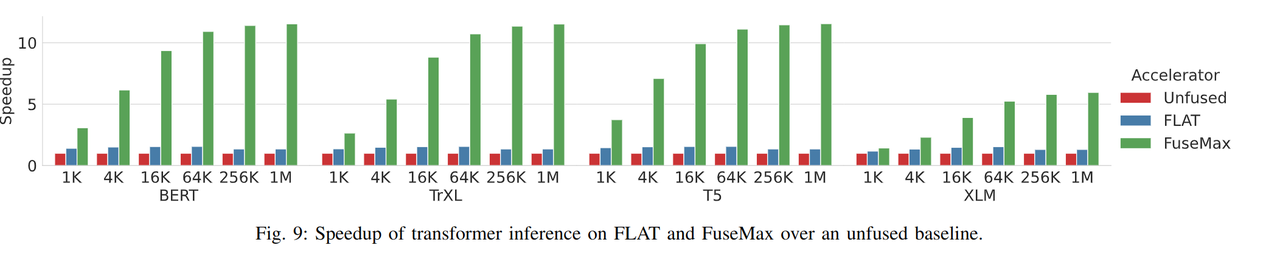
因为计算单元利用率提高，所以加速比也显著提高。

3.4 Energy

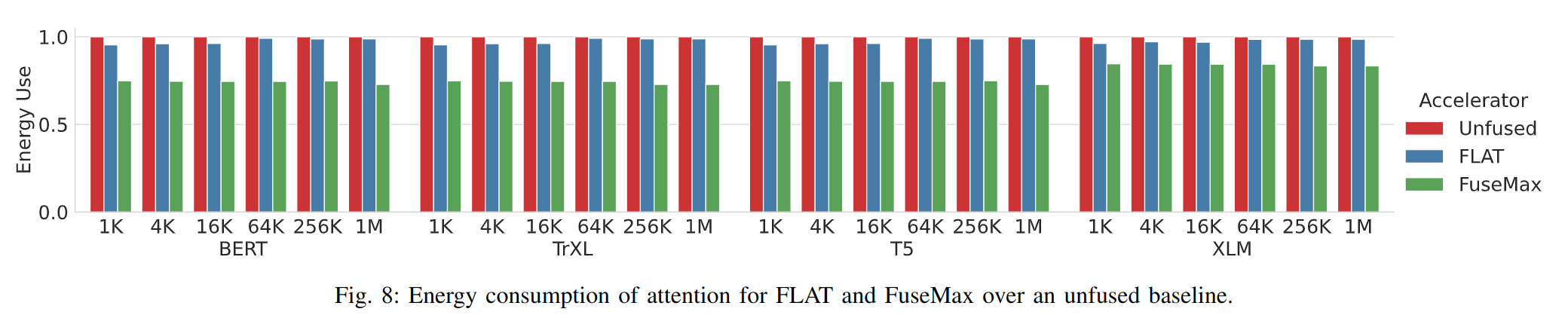
在 attention 时的能耗：

img

在 inference 时的能耗：

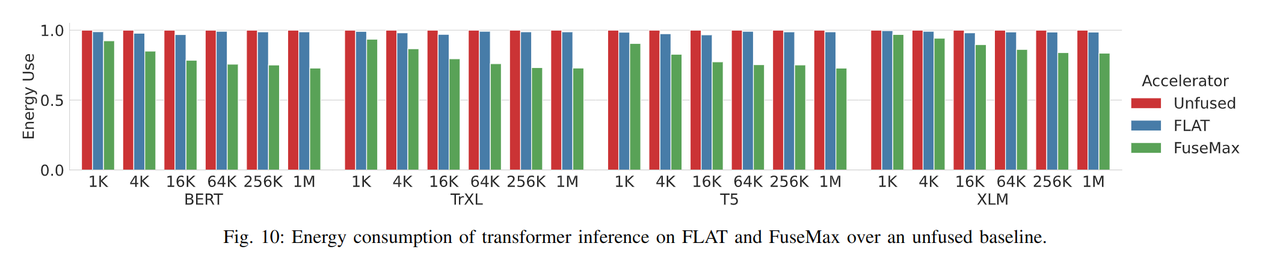
2861afa9-44ca-43ca-ba57-24cee9103951

Flash-Attention 节约了 DRAM 的访存开销。

四、计算密度

这篇工作主要结合了前人的工作，许多成果本质上是算法（Flash-Attention）或者开发框架（TeAAL，Timeloop）的成果，而非这篇工作自己的成果。

随着计算单元数目的增多，Roofline 模型中的硬件的 越来越往右移动，这就导致越来越多的算法成为 memory bound 的：

img

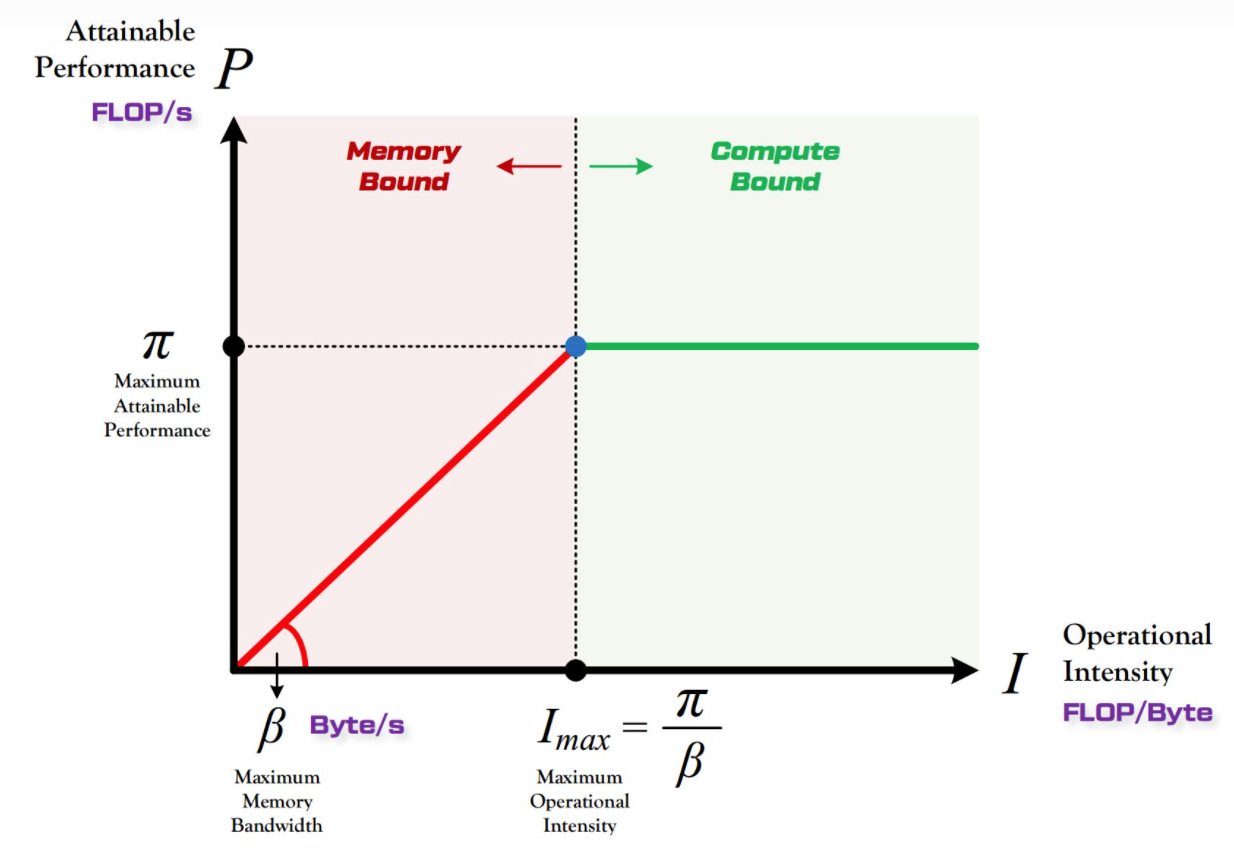
有一种解决问题的方式是减少内存读取的次数，比如说 Kernel Fusion：

img

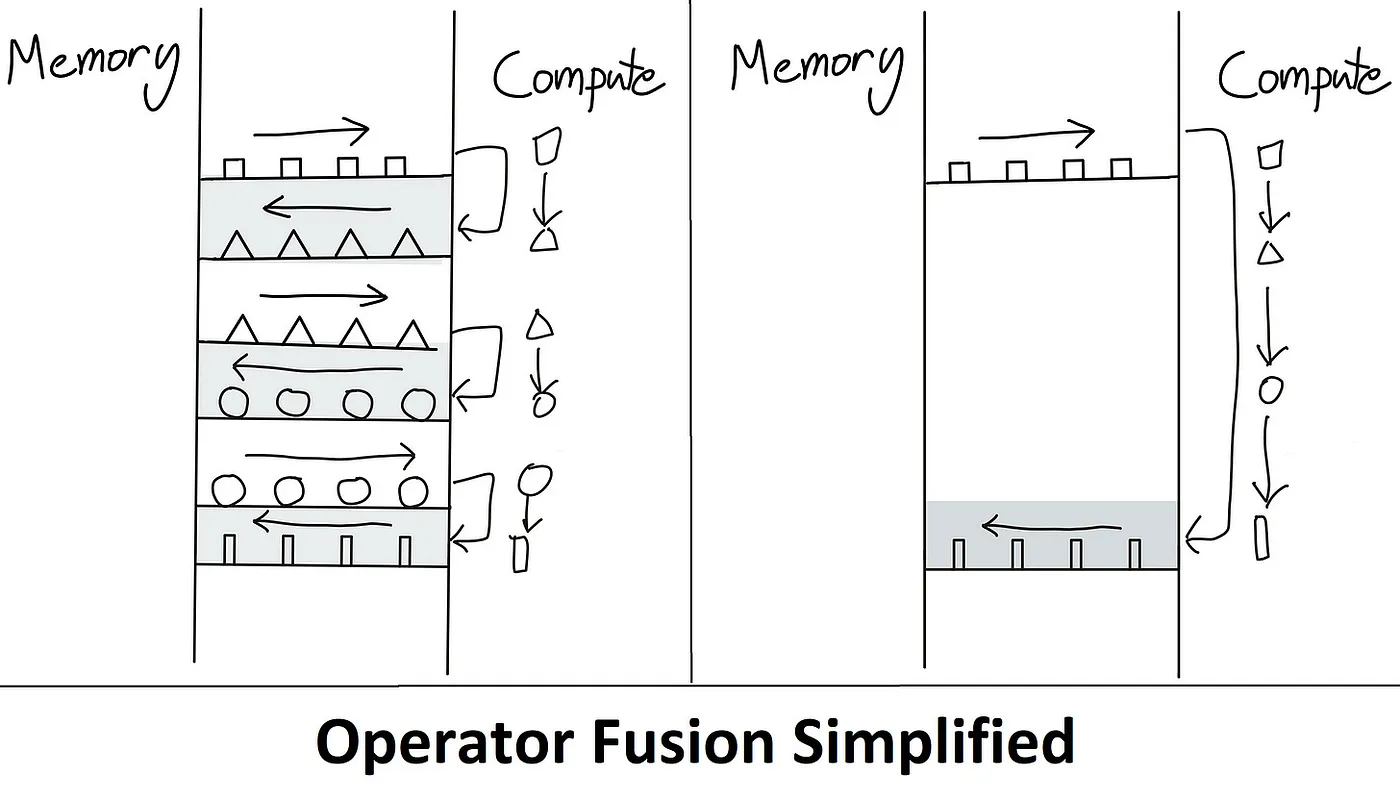
直白的 Fusion 并不会修改算子的实现，它只是将计算的中间结果存在了 On-chip Memory 中，但是 On-chip Memory 空间有限，这就导致一旦存不下来，依然会溢出到 Off-chip Memory 中，最终效果并不好（从上文的 Evaluation 中也可以看出）。

为了解决溢出问题（或者单纯为了减少访存次数），有一种思路是增加 On-chip Memory 的容量，比如说 IPU，相比于 CPU 和 GPU，就增加了更多的片上 SRAM：

img

但是这种方式存在问题，就是片上 SRAM 的面积过大，IPU 很少去和 GPU 对比单位芯片面积（iso-area）下的性能。

Flash-Attention 和 FuseMax 我认为是另一种思路的代表，就是“以算代存”，计算的中间结果并存储后供后续使用，而是当需要使用的时候，再次计算一遍，是一种更加“数据流”的方法。通过构造额外的计算，来避免存储（Flash Attention 引入了更多的冗余的计算，但是减少了冗余的存储）：

imgimg

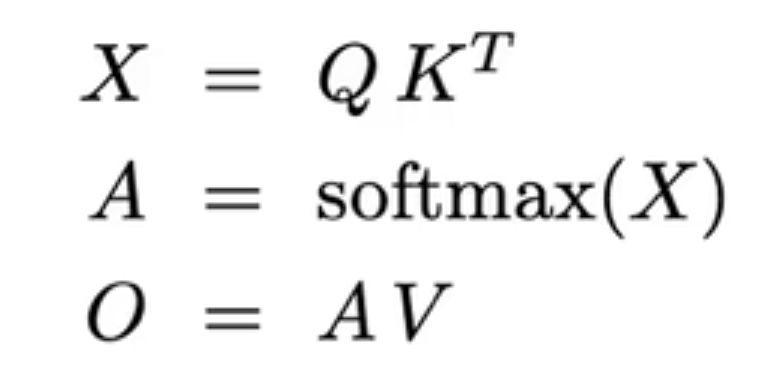
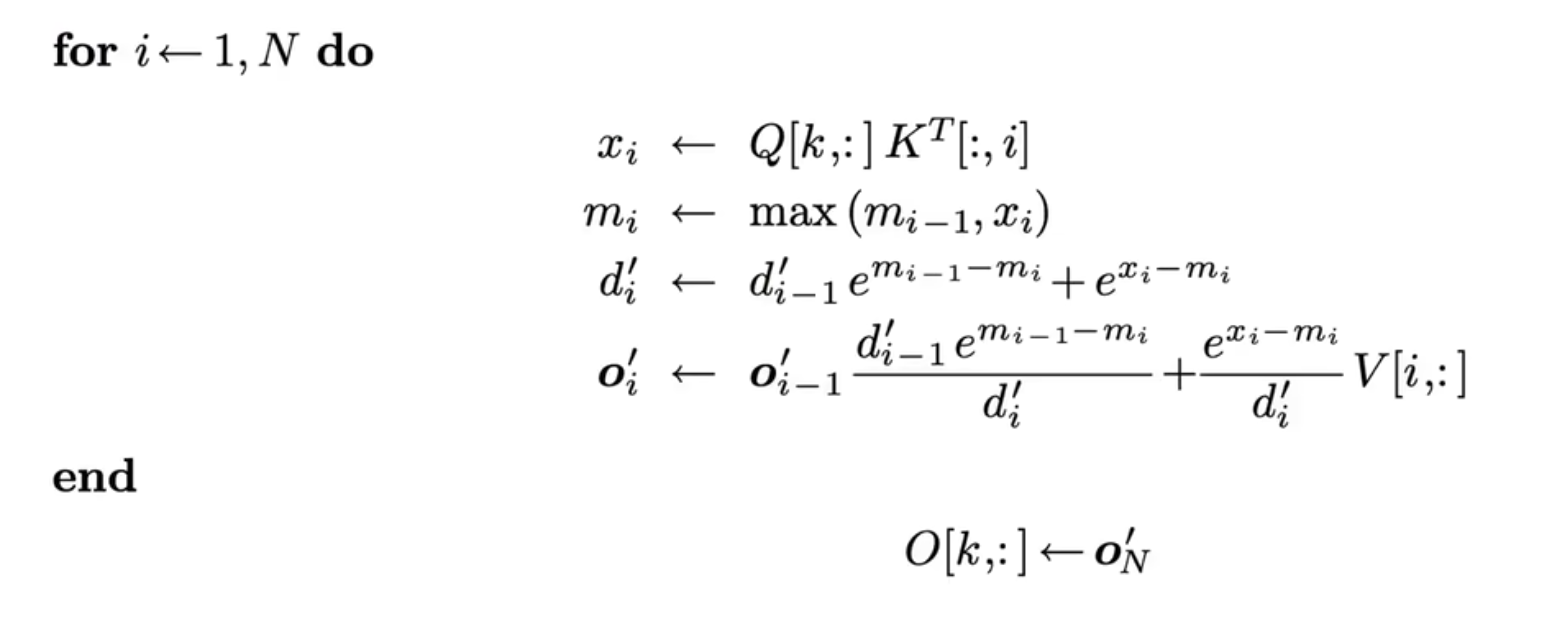
我个人隐隐约约感觉，计算单元和存储单元有某种统一性，如果能把握它并提出一种更好的抽象，或许可以做出一个更本质的 tradeoff。