大学物理-气体动理论

气体动理论是统计物理学的部分内容，那么是怎么体现统计的呢？

每个运动着的分子都有大小、质量、速度、能量等，这些用来表征个别分子性质的物理量的叫做微观量。一般在实验中测得是表征大量分子集体特征的量，叫做宏观量，气体的温度、压强、热容等就是宏观量。气体动理论就是运用统计方法，求出大量分子的某些微观量的统计平均值，并用以解释在实验中直接观测到的物体的宏观性质。

一、理想气体状态方程

$pV = \frac{m}{M}RT$

在这个公式里，需要三点需要强调：

$\frac{m}{M}$ 不可以简写为 $n$ ，这是因为在这本教材里，$n$ 是分子数密度，不是分子的物质的量
$M$ 是以 Kg 为单位的，所以需要比常见的化学单位制小三个数量级，不要在计算的时候出错
$R$ 是普适气体常量，$R = 8.31J/(mol\cdot K)$

理想气体状态方程还有另一个形式，这个形式好像更加强调气体的微观特征。

其中：
- $n$ 是分子数密度
- $k$ 是玻尔兹曼常量，有 $k\cdot N_A = R$，$k = 1.38 *10^{-23}J/K$
- 有 $k$ 出现的地方好像都很微观。

二、压强，平动动能与温度的关系

我们可以用统计规律推导出压强与分子动能的关系，有

$p = \frac{2}{3}n\bar{\varepsilon_k}$

这是一个统计规律，而不是一个力学规律。对于这个式子要多说几句，这个式子看似很简洁本质，但是你会发现，能够影响压强 $p$ 的因素是多个，有分子数密度和分子平均动能，而且，分子数密度还是跟物质的量和体积两个变量有关，也就是说，这个式子很不本质，起码不简洁（这是一个新的概念）。我们能从这个式子能得出的最有效结论只有压强跟分子密度和分子动能（或者温度）成一定的正相关。只是一个直观认识。

当然再结合我们的理想气体状态方程，就会导出动能和温度的关系

$\bar{\varepsilon_k} = \frac{3}{2}kT$

这个公式好就好在，是一个单元的函数，这说明气体的温度是气体分子平均平动动能的量度。

上面这两个式子的推导，都用到了统计学的技巧。

三、自由度与内能

理想气体的内能不只包括平动动能还包括转动动能和振动动能。所谓的平动动能能，就是指我们之前算的 $v_x,v_y,v_z$ 算出的能量，一共是三份。所谓的转动动能是分子转动的能量。这个是因不同分子而异的，比如说单原子分子，就没有转动动能（一个球体现不出转动），对于双原子分子，就有两份转动动能（定轴转动），对于多原子分子，就有三份转动动能（定点转动）。所谓振动动能，就是同一个分子原子间的距离在原子间的相互作用下，会发生变化，分子内部会出现振动。

一般在低温的时候，只有平动起作用，在室温的时候，可能有平动和转动起作用，在高温的时候，可能有平动，转动，振动起作用。但是也要结合具体的分子种类进行考量。

为了更好的概括我们得到的统计规律，我们提出了自由度的概念，即确定物体运动状态所需要的参量数，平动因为是在三维空间中，所以是3个自由度，转动如果是定轴转动，那么是2个自由度，如果是定点转动，那么就是3个自由度。振动自由度也要考虑进去。自由度的符号为 $i $。

能量按自由度均分定理告诉我们：在温度为 T 的平衡态下，气体分子任一自由度的平均动能都等于 $\frac{1}{2} k T$ ，但是需要注意的是，对于每个振动自由度，每个分子除了一份平均振动动能，还有一份平均弹性势能。

按照这个理论，我们有公式

$E_0 = N_A(\frac i 2 kT)=\frac i 2 RT$

这是 1 mol 理想气体内能的表达式。

需要注意的是，理想气体是没有分子间势能的。所以动能就是内能。这句话的意思就是，理想气体的内能是温度的单值函数，这个甚至可以作为理想气体的定义。

四、麦克斯韦速率分布律

最重要的一点，本节讨论的都是速率，也就是速度的模长，这是因为速度的均值一定是0。

$f(v) = 4\pi (\frac{m_0}{2\pi kT})^{\frac{3}{2}}\cdot e^{-\frac{m_0 v^2}{2kT}}\cdot v^2$

这是最基础的形式，其实只需要意识到这是一个 v 的一元函数就好了 $f(v) = a\cdot e^{-bv^2}\cdot v^2$ 。这个式子虽然形式复杂，但是其实他很简洁，因为是一个单变量函数。这个形式有点像黑体辐射的公式，都是有一个极大值点的凸包函数。

其本质是速度分量都是服从正态分布，而且彼此独立。

$v_x \sim N(0,\frac{kT}{m_0}),\quad v_y \sim N(0,\frac{kT}{m_0}),\quad v_z \sim N(0,\frac{kT}{m_0})$

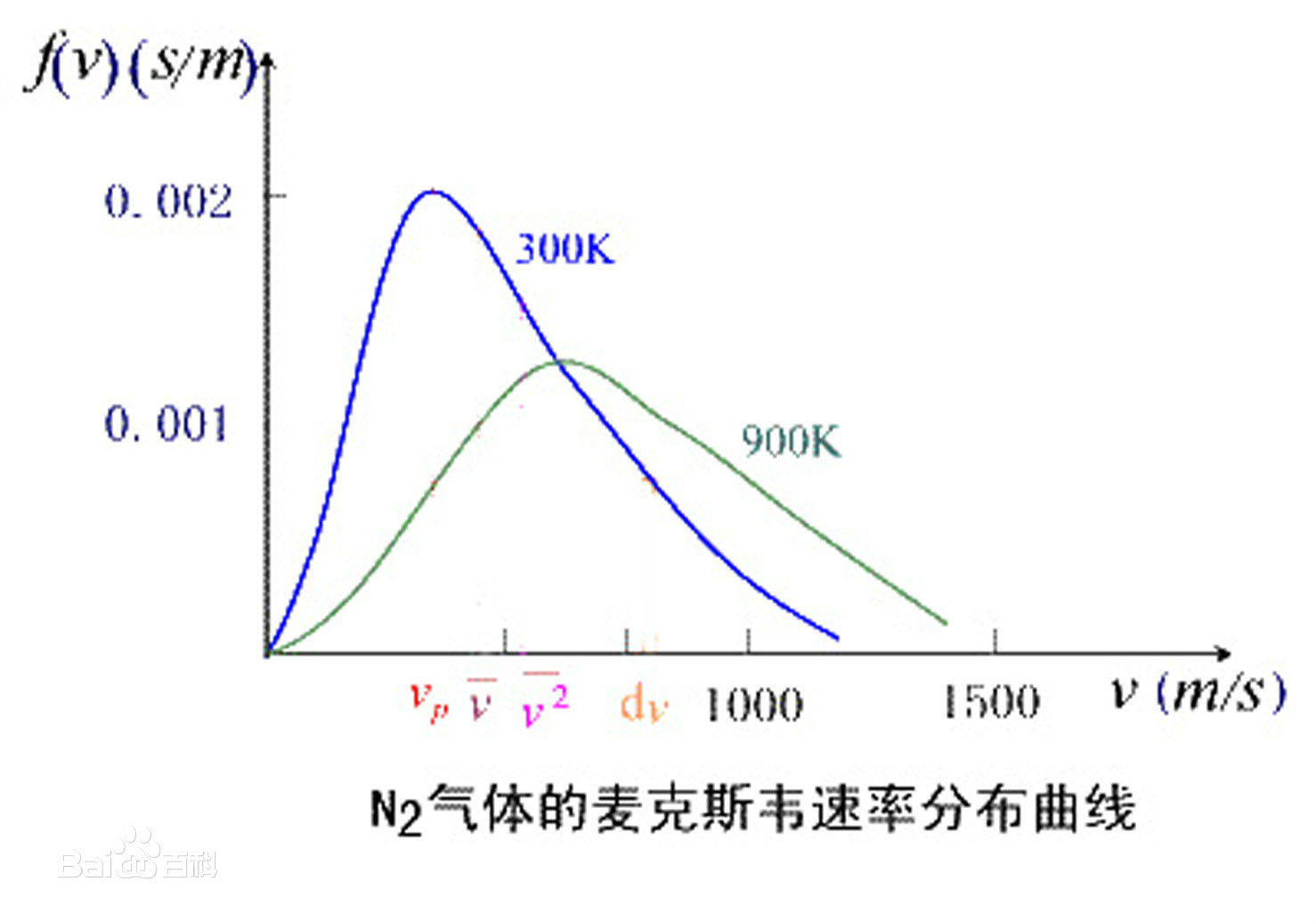
这个分布律其实严格的说，应该是概率密度分布函数。也就是说，这是一个概率论的应用，可以看到下面求平均速率，就是在求期望，而求方均根速率，就是在二阶矩的平方根，方法都是相同的。

由这个式子，我们可以得出一些特殊的值

$\bar v = \int^\infty_0 vf(v)dv=\sqrt\frac{8RT}{\pi M} = 1.60\sqrt{\frac{RT}{M}}$ $\bar{v^2} = \int^\infty_0 v^2f(v)dv = \frac{3RT}{M}$ $v_{rms} = \sqrt{\bar {v^2}} = \sqrt\frac{3RT}{M} = 1.73\sqrt{\frac{RT}{M}}$ $v_p = \sqrt\frac{2RT}{M} = 1.41\sqrt{\frac{RT}{M}}$

其中，$v_p$ 是最概然速率，是用求导获得的，另外两个都可以用分部积分获得。

最概然速率的物理意义是，在一定的温度下，速度大小与 $v_p$ 相近的气体分子的百分率最大，也就是说，以相同的速率间隔来说，气体分子中的速率在 $v_p$ 附近的概率最大。它的物理意义是，在一定温度下，速度大小与 $v_p$ 相近的气体分子的百分率为最大。

为了估算一个狭窄区间的分子数百分比，可以将上式转换成另一种形式，即

$\frac{\Delta N}{N} = f(W)\Delta W = \frac{4}{\sqrt{\pi}}\cdot W^2 e^{-W^2}\Delta W$

其中 $W=\frac{v}{v_p}$，其实就是以直代曲的思想。

其实上面的公式还不是最本质的公式，最本质的公式是

$\Delta N = n_0(\frac{m_0}{2\pi kT})^\frac 3 2 e^{-\frac{\varepsilon}{kT}}\Delta v_x \Delta v_y\Delta v_z\Delta x\Delta y\Delta z$

其中 $n_0$ 是某个基准点的气体分子密度。$\Delta N$ 是分子数。

在麦克斯韦能量分布律中，将 $\varepsilon$ 视为 $\varepsilon_k$ ，并且只对位置分量进行积分，就可以得到最上面的式子。

五、玻尔兹曼能量分布律

玻尔兹曼是将速度量进行积分，就可以得到玻尔兹曼分布律

$\Delta N = n_0 e^{-\frac{\varepsilon_p}{kT}}\Delta x\Delta y\Delta z$

注意这里的 $\varepsilon_p$ 是分子的势能，但是不是分子间势能，所以这依然是相对于理想气体而言的。将其转换为更常见的形式（结合重力势能表达式）

$n = n_0e^{-\frac{m_0gz}{kT}}$

如果再结合 $p = nkT$ 就可以得到

$p = p_0e^{-\frac{Mgz}{RT}}$

这个用宏观量压强 $p$ 代替分子数密度 $n_0$ 的操作之后还有，这可能是一种思想吧。

六、分子碰撞和自由程

自由程的意思就是分子没发生与其他分子碰撞的路程，也就是每两次连续碰撞间分子自由运动的平均距离（注意这里也是用到了统计的思想）。当自由程变大的时候，说明要么是碰撞频率减少了，要么是分子运动速度快了。平均自由程的符号用 $\bar{\lambda}$ 表示。

为了计算平均自由程，我们首先要计算平均碰撞频率，计算它的思想就是假设除一个分子外的其他分子都静止不动，只有那一个分子一平均相对速度 $\bar{v_r}$ ，那么每秒这个运动的分子扫过的体积就可以求出来，然后在这个体积内的其他分子数目也可以求出来，这些其他分子都是会被碰撞到的，所以其数目就是平均碰撞频率。我们有公式

$\bar{Z} = \pi d^2 \bar{v_r} n$

我们又有平均相对速率与平均速率的关系：

$\bar{v_r} = \sqrt2 \bar{v}$

于是就可以推导出来了，我们之所以再次进行变换，引入压强 $p$ ，可能是因为压强是一个宏观量

$\bar Z = \sqrt2 \pi d^2 \bar v n =\sqrt2 \pi d^2 \bar v \frac{p}{kT}$ $\bar\lambda = \frac{\bar{v}}{\bar{Z}}=\frac{kT}{\sqrt{2}\pi d^2 p}$

可以看出，当温度一定的时候，$\bar{\lambda}$ 与 $p$ 成反比，压强越小，则平均自由程越长。

当分子相距极近的时候，他们之间的相互作用力是斥力，分子间的相互斥力开始起显著作用的时候，两分子质心间的最小距离的平均值就是 $d$ 。所以 $d$ 叫做分子的有效直径。