一、总论
乱序指的是指令并不按照顺序执行,所以这个概念比较接近软件编程中的“异步”概念(强调对于顺序时序的破坏)。而我之前似乎一直把它和“并行”挂钩(强调对于共享资源的争用)。这种认识倒也不算是错误,目前学了一圈下来,感觉其实和两个概念都有关系。
在顺序模型下,指令是一条条阻塞执行的,必须前一条指令执行完,才能执行后一条指令。那么如果前一条指令非常花时间,那么后一条指令就只能阻塞等待。这个问题是用流水线解决不了的。流水线中的指令也需要顺序执行。而乱序执行就打破了这种顺序执行的阻塞性,使得前序和后序指令可以并行执行。
二、冒险(hazard)
我们希望 CPU 按照理想情况运行,那么什么是理想情况?对于单个处理器核心,当:
时就是理想情况了。而在现实生活中,常常因为多种现实因素使得指令的执行速度减慢,这些现实因素被称为“冲突(hazard)”。具体有 3 种:
- 结构冲突(structure):指的是对于功能单元的竞争情况,比如两个指令都需要 ALU,而只有一个 ALU,那么这两条指令就只能串行。
- 分支冲突(branch):指的是因为分支而导致的指令流中断,比如突然发现正在执行的指令属于不会被执行的分支,那么这些指令都需要撤销。
- 数据冲突(data):指令需要的数据还没有被前一条指令计算出来,那么就会导致阻塞。
CPU 种有很多功能单元(也可以看作计算资源),我们希望让他们都运转起来,不要闲置或者做无用功。但是每条指令并不会“同时”使用这些资源,比如对于一条指令的执行,只要取出指令后,就不需要再从 I-Cache 中读值了,当这条指令让 ALU 进行运算的时候,Fetch,Decode,Write Back 这些单元是闲置的。所以我们发明了流水线技术,将功能单元划分到不同的流水级,每个流水级都运行一条指令,这样就可以并行利用不同的资源。但是这样还不够,因为可能一个阶段里还有很多个功能单元,比如说 Execute Stage 里就有整数计算单元,浮点数计算单元,访存单元等,这些单元想要满载运转,就不能再采用流水线技术了,因为这些资源并不是每条指令都会用到,如果我们将 Execute Stage 拆分成 Calculate Stage 和 Memory Stage ,那么 Memory Stage 的资源就会在执行计算指令时被闲置,而 Calculate Stage 的资源则会在执行访存指令时被闲置,所以我们可以采用乱序的方式,让一个流水级中包含多条指令,比如 Execute Stage 就可以同时包含一条计算指令和一条访存指令,这样资源就可以得到更充分的利用。
总得来说,我们可以利用流水线技术和乱序技术对 CPU 内的资源进行不同维度的并行操作:
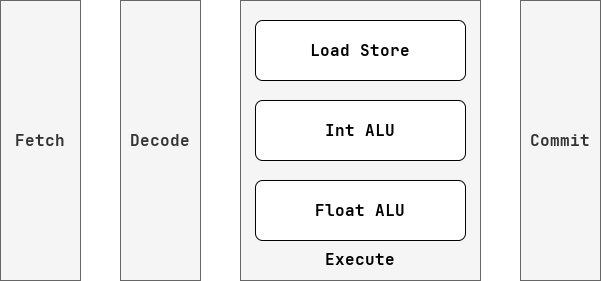
从这个角度看,流水线深度并不是越深越好,因为被时序分割的资源,并不会在每条指令上得到充分利用,反而是乱序的方式,更能充分利用资源。
总得来说,我们对于明显有依赖关系的资源,会采用流水线的方式来并行,比如说取指单元和译码单元的流水线处理;而对于没有依赖关系的资源,我们会采用乱序的方式并行,比如访存单元和计算单元的乱序。更进一步辩证地看,在同一级流水线中,一定存在没有依赖关系的资源,那么就是可以乱序的;在
三、算法
我觉得我自己之所以谈到更加高级的 CPU 特性,比如说乱序、分支预测谈虎色变,是因为我在心里认为在硬件上是没有办法实现过于复杂的算法的。但是这种观点是很不精确的,硬件和算法的复杂程度没有必然联系,不过确实在硬件上实现的算法会有一些硬件特征。
首先是在 CPU 中是没有内存的,所以也就没有地址。这里很容易产生一个误导,就是同样没有指针。这是不对的,算法需要的并不是一个具体的指针,它只需要一个“指向某个数据的变量”即可,所以没有指针,也可以用整型索引代替。这有点像算法竞赛在实现链表,树之类的数据结构的时候,都不会使用指针,而是提前开一个大数组,然后用索引来指向其中的元素的思想。
然后是在 CPU 中没有像高级语言的“无限”概念的,任何资源都是有数量限制的。不仅是资源的数量有限制,资源的规模也有限制,比如说一个整数寄存器,就是 32 位,如果希望表达一个更大的数,那么就没有办法了。不过这种限制其实很好解决,只需要阻塞 CPU 直到相关资源富裕就可以了,常见的问题有空闲物理寄存器数目不够,指令编号溢出,队列溢出等。
还有一种解决资源有限的方法,是将资源的状态都保存到内存中,不过这种方法在微体系结构中用得不多(时间开销太大),但是在编译器开发中很常见。
最后是 CPU 上的算法的局部性很强,而且是只有一遍的,我们只能看到 CPU 上运行的这几条指令,或者还有一些 buffer 指令,而且只能看见一次。这就导致很多全局算法我们是没有办法直观实现的,但是我们可以采用一种像“流”或者是“滑动窗口”的思想去从局部推断全局。
总得来说,CPU 的性质使得它在描述算法或者数据结构的时候,会呈现一种朴素的,有限的、狭隘的特征,但是基本上没有算法是用 CPU 无法表示的(复杂的森林和图都是可以的),所以当我们去看 CPU 上的特征时,应当从它笨拙的表达中,看出其背后的精妙算法。
四、假冒险
这里讨论的真假冒险都是数据冒险的一种,其实就是对于数据依赖关系的讨论。出现数据冒险问题,是优于前序指令(一个装逼的说法,就是在汇编中位置靠前的指令)晚于后序指令提交造成。
所谓的真冒险,就是“写后读”(Read After Write,RAW),吐槽一句,可以发现在中文这个词是先写后读,而在英文中变成了下先 R 后 W,刚好是反过来的,后面我只用英文。至于为什么它是真冒险,是因为只有前序指令写入了这个数据,后序指令才能读入新的值。
write r0
read r0 # commit first, error与之相对的,有 WAR 和 WAW 两种假冒险。对于 WAR 而言,先序指令读,后序指令写,我们担心的是,后序指令先提交的情况,但是如果后序指令没有提交到原本的寄存器中呢,那么就不存在问题了,换句话说,如果有无限个寄存器(类似于无限个变量),那么谁还为了省一些寄存器,而去覆盖一个可能还会被读的寄存器。
read r0
write r0 # commit first, error
### good ###
read r0
write r1 # commit first, correct至于如何让寄存器变成无限个,那其实就又很多种办法了,大不了阻塞 CPU 嘛。当然在实际应用中,我们会通过重命名的手段,在内存中维护一个从逻辑寄存器到实际寄存器的映射关系,来使得不会发生依赖现象,这就是寄存器重命名。
而寄存器重命名算法,在原理上和编译器的寄存器分配算法的需求是一样的,唯一的区别在于编译器的逻辑寄存器不够了,那么就会往栈上存,而 CPU 的物理寄存器不够了,就会阻塞 CPU。当然了,像图着色或者线性扫描这种方法是没法用到 CPU 上,CPU 一般就是维护一个空闲寄存器队列就够了。
五、计分板
从任何意义上说,寄存器就是内存的一个过客。
如果我们拨开 ISA 的复杂性的迷雾,就会发现 CPU 的核心在于“读入内存,计算,写入内存”的图灵机模式,其中的计算步骤,其实就是构建一个计算的 DAG 图(有向无环图),其结构如下:
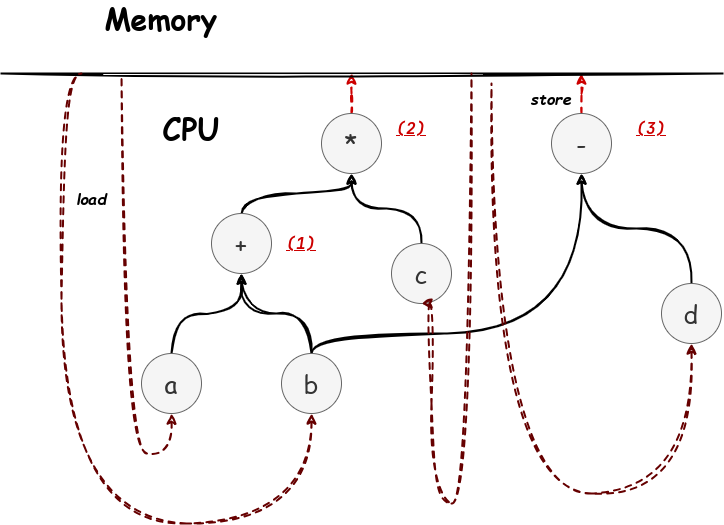
寄存器的作用就是存储这些 DAG 图的中间节点。这里面的 (1), (2), (3) 可能就分别对应某个寄存器。
所谓的计分板,就是描述这幅图的数据结构,他的每个条目就是图上的一个点
| ID | ready | child |
|---|---|---|
| (1) | false | a, b |
| (2) | false | (1), a |
| (3) | true | b, d |
那么为什么要保留这样的一个结构,因为这个结构非常方便查看是否允许并行并处理相关的数据依赖。
比如在计分板上,我们就知道 (2) 这条指令还没有办法进行计算,因为 (1) 还没有算完,但是 (3) 已经可以算了,也就是 (1), (3) 可以并行计算,而 (2) 不可以。我们还可以看出 (1), (3) 都依赖 b 这个节点。而且这里的 ID 可以理解成一种逻辑寄存器,我们可以将其分配给物理寄存器。
总之计分板就是这样的一个全局看板结构,基于 DAG 图的方式来协调乱序并行。