一、BFS 模板
如下所示
set<Node> visited;
bool check(Node son);
int bfs(Node start)
{
// init
queue<Node> q;
q.push(start);
visited.insert(start);
while (!q.empty())
{
Node front = q.front();
q.pop();
for (son : q.neigbour)
{
// prune
if (check(son))
{
q.push(son);
visited.insert(son);
// son is the correct answer
if (ac(son))
{
return son.info();
}
}
}
}
return -1;
}
int main()
{
//...
int ans = bfs();
//...
return 0;
}其中有几部分需要一一强调,第一个是 check() 函数用于进行减枝,只有经过 check 的子节点会被加入队列。
bool check(Node son);check 的基础内容就是有没有被 visited 过,其写法如下
visited.count(son) == 0
visited.find(son) == visited.end()这两种写法都表明 visited 中没有 son 。
另外就是有的时候 BFS 的遍历会伴随着诸多与 Node 对应的数据的记录,比如说每个 Node 对应的 level 这样的信息,建议使用一个(或者多个)全局的 map 去这样存储
map<Node, Info> levels;而一旦存在这样的 map,那么就可以省略 visited 了,因为没有必要了。判断是否存在,可以用
levels.count(son) == 0;
levels.find(son) == visited.end();同时当我们使用 BFS 的时候,我们一般是希望获得最优解(对应最小的 level),所以我们一般就遍历到合适的 Node ,就需要返回了,所以我们应当将 BFS 写成一个函数,然后方便 return 跑路。但是这就要求 BFS 需要的变量尽量是全局变量,方便访问。
二、双向 BFS
其思想是,如果 BFS 的起点和终点是可以确定的,那么就分别从起点和终点进行 BFS,最终的判断条件是两棵树是否相交(本质是两个 visited 相交),这样做的好处是可以去掉大量的无用的遍历,同时保有了 BFS 的特性
单向搜索:
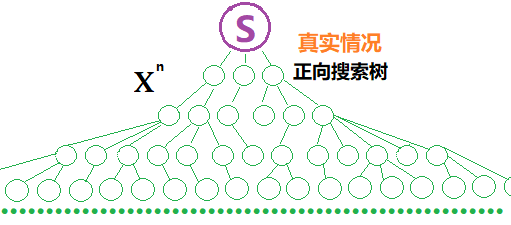
双向搜索:
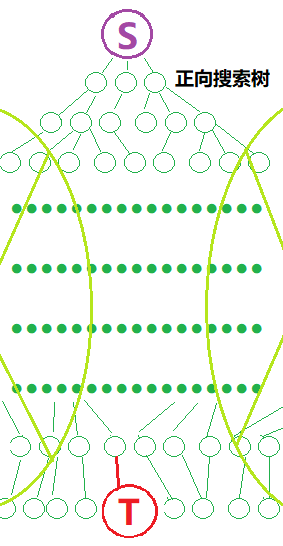
其在实现上基本上就是普通 BFS 复制一遍,唯一需要注意的就是利用 visit 相交的判断,板子题如下
[NOIP2002 提高组] 字串变换
题目描述
已知有两个字串 $A,B$ 及一组字串变换的规则(至多 $6$ 个规则),形如:
- $A_1\to B_1$。
- $A_2\to B_2$。
规则的含义为:在 $A$ 中的子串 $A_1$ 可以变换为 $ B_1$,$A_2$ 可以变换为 $B_2\cdots$。
例如:$A=\texttt{abcd}$,$B=\texttt{xyz}$,
变换规则为:
- $\texttt{abc}\rightarrow\texttt{xu}$,$\texttt{ud}\rightarrow\texttt{y}$,$\texttt{y}\rightarrow\texttt{yz}$。
则此时,$A$ 可以经过一系列的变换变为 $B$,其变换的过程为:
- $\texttt{abcd}\rightarrow\texttt{xud}\rightarrow\texttt{xy}\rightarrow\texttt{xyz}$。
共进行了 $3$ 次变换,使得 $A$ 变换为 $B$。
输入格式
第一行有两个字符串 $A,B$。
接下来若干行,每行有两个字符串 $A_i,B_i$,表示一条变换规则。
输出格式
若在 $10$ 步(包含 $10$ 步)以内能将 $A$ 变换为 $B$,则输出最少的变换步数;否则输出
NO ANSWER!。样例 #1
样例输入 #1
abcd xyz abc xu ud y y yz样例输出 #1
3提示
对于 $100\%$ 数据,保证所有字符串长度的上限为 $20$。
【题目来源】
NOIP 2002 提高组第二题
此时的题解如下
#include <bits/stdc++.h>
using namespace std;
string a[10], b[10];
int main()
{
string origin, target;
cin >> origin >> target;
// 不定长输入
int n = 0;
while (cin >> a[n] >> b[n])
{
n++;
}
// 分别代表两个队列,分别从 up 和 down 两个方向搜索
queue<string> up, down;
// 记录字符串和步数的关系,同时兼具 visit 的功能
map<string, int> upStep, downStep;
// 入队起始节点,并登记
up.push(origin);
upStep[origin] = 0;
down.push(target);
downStep[target] = 0;
// 搜索的次数最多是 10 次,所以双向 5 次
for (int step = 1; step <= 5; step++)
{
// 先进行 up 向下搜索
// 限制当前处理的都是 step - 1 层
while (upStep[up.front()] == step - 1)
{
string front = up.front();
up.pop();
// 遍历所有的转换规则
for (int i = 0; i < n; i++)
{
// 寻找所有位置的 a[i] 进行替换,pos 是可替换字符串子串出现的位置
for (int pos = front.find(a[i]); pos != -1; pos = front.find(a[i], pos + 1))
{
// tmp 是利用 a[i] -> b[i] 规则的字符串
string tmp = front;
// replace(pos, len, str) 从 pos 开始替换 len 长度的 str
tmp.replace(pos, a[i].length(), b[i]);
// 当 find 找不到的时候,会返回 end() 迭代器,此时说明没有 visitUp
if (upStep.find(tmp) == upStep.end())
{
// 入队
up.push(tmp);
// 登记
upStep[tmp] = step;
}
// 在对面找到了,所以一共花了 step * 2 - 1 步
if (downStep.find(tmp) != downStep.end())
{
// 搜出答案就可以结束了,从这里可以看,最好把 bfs 写成一个单独的函数,否则会非常丑陋
cout << step * 2 - 1;
return 0;
}
}
}
}
// down 向上搜索
while (downStep[down.front()] == step - 1)
{
string front = down.front();
down.pop();
// 遍历所有的转换规则
for (int i = 0; i < n; i++)
{
// 寻找所有位置的 b[i] 进行替换,pos 是可替换字符串子串出现的位置
for (int pos = front.find(b[i]); pos != -1; pos = front.find(b[i], pos + 1))
{
// tmp 是利用 b[i] -> a[i] 规则的字符串
string tmp = front;
// b[i] -> a[i]
tmp.replace(pos, b[i].length(), a[i]);
// 当 find 找不到的时候,会返回 end() 迭代器,此时说明没有 visitUp
if (downStep.find(tmp) == downStep.end())
{
down.push(tmp);
downStep[tmp] = step;
}
if (upStep.find(tmp) != upStep.end())
{
cout << step * 2;
return 0;
}
}
}
}
}
cout << "NO ANSWER!";
return 0;
}需要注意的是,这里用了固定迭代次数来进一步减枝,但是这并不是 BFS 的必要特征。