有些东西可能是离散数学这门学科的通病。相比于高数或者线代,有一定在物理上的应用场景,而且其精神,比如说无穷,比如说代数系统,很容易被理解,而且很容易为我所用。离散这门学科没有一个中心,没有一个明确的思想(也可能是我没有发现),没有具体的应用场景(可能在算法里有用吧),学科的体系感也不强(可能是我接触的比较浅的缘故)。正因为如此,图论才如此难学,而且我参考了三本书,有的时候三本书对于同一个定义都具有不同的诠释,这更使我觉得,我没有搞清楚离散到底在研究什么?这个核心问题,许多困难与辨析,都是因为诸多“表象”,而通过表象洞彻本质,才能从万变中发现永恒。而这些都是我没有做到的,所以我写下了这篇文章,希望可以边写,边领悟其中的真意。
图的最本质内容是一种二元关系。
为了直观形象地理解图的结构和性质,总是用图形来表示一个图。
这句话是否说明,“图并不本质”,我们去对一个客观事物建模的时候,不应该先用他是不是一个图来考量,而是应该用他是不是一个二元关系来考量。这或许是一个很好的点。
图作为一个数学概念,其可以用来描述的客观事物一定是不胜枚举的。但是仅仅用图去描述现实中的地图、人际关系网,是不是有点形而下学了。如果用图俩描述流程图,或者解题图,会不会别有一番天地。突然想到,马尔可夫链也可以看做是图的一个应用,每一个随机过程,对应一个路径。
王兵山三元组图一生黑!!!
一、描述图
1.1 图的组成
这里存在两种说法,一种是认为图是一个由节点和边组成的二元组 $(V,E)$,对于无向图来说,边是一个含有两个顶点的集合,而对于有向图来说,边是一个含有两个节点的序偶。这种说法比较符合我们的直观认知,但是有一个缺陷,就是对于平行边,也就是起点和终点相同的边,这种描述就很难区分这种情况。所以有了王兵山三元组定义,也就是 $(V,E,\Psi)$ ,包括节点,边,和映射关系,这种映射关系并不要求双射,所以可以把不同的边映射到相同的起点和终点的集合或者序偶中。
1.2 关系的描述
关联:描述的是顶点和边的关系,顶点是边的终点或者起点,那么这个边和这个点就是关联的。
邻接:描述的是顶点和顶点,边和边之间的关系。如果点与点之间通过边连接,那么这两个点就是邻接的。如果边与边通过顶点连接,那么这两个边就是邻接的。
度:用来衡量顶点的关系的多少的一个量,在有向图中,又分为出度和入度。为什么要引入这么一个度量呢,是因为这个度量比较弱,我们知道度,但是还不知道这个图具体什么样子,但是同时又比较强,因为图就那么几种,知道了度的信息,就可以发现一些规律了。宽松的说,各个节点度越高的图,边数越多。如果反应到图的矩阵表示法,度其实是对矩阵的行或者列的元素的求和。
1.3 特殊的节点、边、图
1.3.1 特殊的点
孤立点:度为0的节点被称为孤立点。
端点:度为1的节点被称为端点。
1.3.2 特殊的边
自圈:如果边的起点和终点都相同,那么就称这条边为自圈。
平行边:如果两条边的起点相同,而且终点相同,那么就称这两条边为平行边。
1.3.3 特殊的图
简单图:如果一个图既无自圈,又无平行边,那么就称这个图为简单图。简单图其实是一个很好的条件,他使得鸽巢原理,反证法等一系列证明方法得以应用。可以说,我们后面大部分的篇幅,都讨论的是简单图的性质。这也使得三元组的定义形式,显得那么的冗余。
零图:节点都是孤立点的图称为零图。零图可以有很多个节点,但是每个节点之间都没有边(即“零边图”)。
平凡图:只有一个节点的图被称为平凡图,这个具体应用的时候常以非平凡图的形式在题目描述中出现,主要是为了排除这种特殊的情况。
d 度正则图:所有节点的度均为 d 的图被称为 d 度正则图。
完全图:如果有 n 个节点的图是 n - 1 度的正则图,那么就称这个图为完全图,记为 $K_n$ ,如果是完全有向图,那么就是出度和入度均为 n - 1。
1.4 图同构
具有 n 个节点的图称为 n 阶图。
图同构的概念就很好理解,所以就不说了,关键是有一个直观认识,就是其实当 n 较小的时候,同构图的种类挺少的。
此外,如果是同构的图,那么其矩阵表示经过行列变化,是可以化成一个相同的矩阵的。
1.5 子图
1.5.1 子图和真子图
我们引入子图的概念乍一看上去是为了研究局部图,可是局部图是很有讲究的,因为图里面既包括点,有包括边,那么到底谁是局部,我认为,我们研究的对象其实是边,或者说,是以边为主体开展研究的。这种感觉很玄妙,我难以说明白。
真子图的要求是只限制边的,边必须是母图的真子集。而并没有对点做出任何要求。
1.5.2 生成子图
生成子图要求顶点集必须与母图的顶点集相等,然后其他并无要求。也就是说,我们将母图删去任意条边,或者不删除边,都可以得到生成子图。可以看出,生成子图描述的是去掉一些联系后,之后的个体的状况。生成子图的连通性会变差或者不变。
1.5.3 导出子图
导出子图更像是一种基于原图构造新图的方式。一共有两种构造方式,一个是基于点集。我们选择母图的点集的一个子集,所以与这个子集相关联的边都会被放到这个新图中。另一个是基于边集,我们选择边集的一个真子集,然后所有与这个边集相关联的点,都会被放到这个新图中。
我虽然觉得生成子图和导出子图很有用处,但是实际是,在后面的证明题中,他们并没有发挥任何作用,可能再以后的应用中他们会比较起作用吧。
1.6 图的运算
这其实对应另一种构造图的方式。
1.6.1 图的可运算性
这个的定义挺有意思的:
满足上面这个条件就称为可运算,这个条件看着唬人,如果是二元组,那么所有的图都是具有可运算性的,但是因为三元组每个边都是由标号的,所以必须要保证映射关系的相等才可以。
1.6.2 不相交
如果有 $E\cap E^\prime = V\cap V^\prime = \emptyset$。那么就说这两个图是不相交的,但是需要强调的是,即使是不相交的,依然是可以运算的。
如果有 $E\cap E^\prime = \emptyset$。那么就说这两个图是边不相交的,从后面的补图的概念我们就可以看出,图和他的补图就是边不相交的,而不是不相交的。
1.6.3 运算
我觉得重要的只有环和和补图,具体的可以参照教材上的定义。
1.7 图的矩阵表示
1.7.1 邻接矩阵
邻接这个词就是说的是点与点的关系,所以如果两个点之间有 n 条边,那么对应的矩阵元素就是 n 。后面还有一个用矩阵的 n 次幂表示路径长度为 n 的路径有几条的公式,都挺好理解的,就不赘述了。
1.7.2 路径矩阵
这个名字就很不直观,他还有另一个名字叫做可达性矩阵,其实就是一个bool值矩阵,如果两个节点之间是可达的,那么对应矩阵元素就置 1,否则就置 0。都是很直观的。唯一一个需要留意的,就是我们可以用邻接矩阵来计算路径矩阵,公式如下
这个利用了阶为 n 的图中,基本路径的长度最大为 n - 1的性质。
1.7.3 关联矩阵
关联说的就是点与边的关系,关联矩阵的行对应着顶点,列对应着边。当其为有向图的时候,元素可以取1,-1, 0。当其为无向图的时候,元素可以取0,1。
还有一点就是关联矩阵可以包括图的全部信息,而另外两个矩阵并没有这种能力。
二、连通性
图的最基本性质之一就是它是否连通。
2.1 路径
这个部分写的很糟糕,各个教材并没有一个统一的概念名词,导致出现了各种混淆的情况,我学的很不好。
2.1.1 简单路径和基本路径
简单路径是指边不重复的路径,而基本路径是指点不重复的路径,基本路径是更强的条件,可以推导出简单路径。我一直怀疑简单路径这个定义存在的必要,它并没有任何应用。
基本回路是有长度限制的,他的最大值是 n - 1。
2.1.2 回路
如果一条路径的起点和终点相同,那么他就是一条回路,也叫做闭路径。让人生气的是,王兵山的书上,对于回路的定义居然是连通的2度正则图,十分的不直观。
2.1.3 完备性
如果一条路径,其中包含了所有的顶点,那么就称它具有完备性。需要注意的是,一个完备的回路,并不一定是一个欧拉回路,因为它不一定遍历了所有的边,也不一定是一个哈密顿回路,因为他可能遍历了一个点很多遍,比如那种花朵一样的图。但是一个欧拉回路或者是一个哈密顿回路一定是一个完备回路。
2.1.4 半路径
如果在一个边的序列中,每个边和序列中下一个边相邻,但是方向不一定一致,那么就称这样的序列为半路径(严格的定义我不想说了,三元组定义太恶心了)。
2.2 无向图分支
分支就是极大连通子图。这里的极大容易让人产生歧义,尤其是王兵山的书,过分强调了唯一性。但是其实任何一个不连通的图中最少有两个分支。
2.3 有向图分支
2.3.1 强连通分支
如果对于每一对顶点 $u,v$ ,都可以由 $u$ 到 $v$ ,并且由 $v$ 到 $u$ 。那么,就称这个图是强连通的。
有向图有一条完备回路,当且仅当它是强联通的。
2.3.2 有向连通分支
如果对于每一对顶点 $u,v$ ,都可以由 $u$ 到 $v$ ,或者由 $v$ 到 $u$ 。那么,就称这个图是有向连通的。
有向图有一条完备通路,当且仅当它是有向连通的。
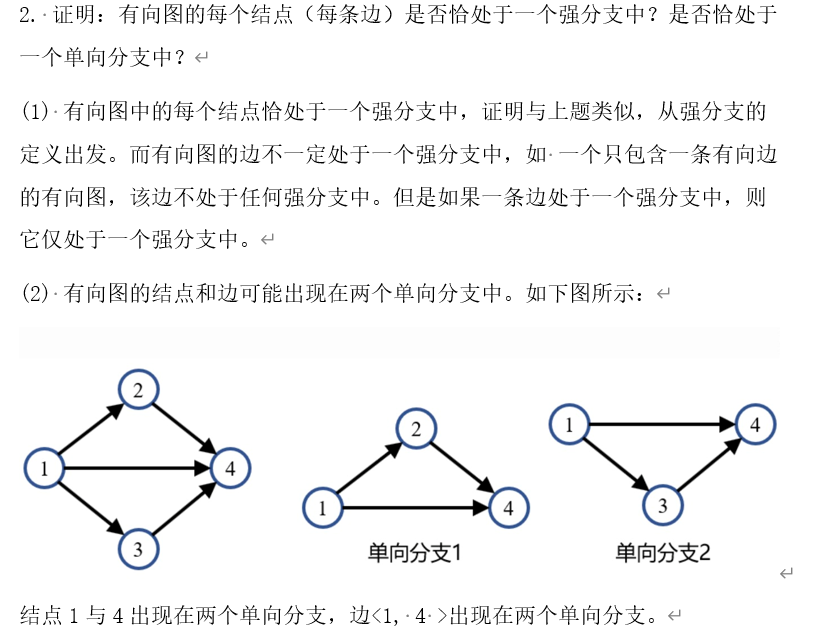
2.3.3 弱连通分支
当有向图的基础图是连通的,那么这个图就是弱连通的。
有向图有一条完备的半通路,当且仅当它是弱联通的。

结合出度用到了鸽笼原理

三、穿程问题
连通性不关注是怎样连通的,只关注是否连通,这是其与穿程问题最明显的区别,穿程问题对于过程的要求较高。如果以解题来举例,那么连通性回答的是可不可解的问题,而穿程问题回答的是怎样求解的问题。
3.1 欧拉图
如果每个节点都是偶节点,那么这个图就是欧拉图。注意,这里并没有强调连通性的问题,所以有可能一个欧拉图没有欧拉回路。
如果一个连通图图只有两个奇节点,那么这个图存在一个欧拉路径。
设G是非平凡的连通无向图,G是欧拉图当且仅当G是若干个边不相交的回路之并
G是非平凡的弱连通有向图,G是欧拉有向图,当且仅当G是若干个边不相交的有向回路之并。
3.2 哈密顿图
3.2.1 充分条件
3.2.1.1 基础图为完全图的有向图
基础图为完全图的有向图必有哈密顿回路

3.2.1.2 欧尔定理
如果 $G$ 是一个有 $n$ 个顶点的简单图,其中 $n\geq3$ ,并且对 $G$ 中每一对不相邻的顶点 $u,v$ 来说,都有 $d(u)+d(v) \geq n$ 。那么 $G$ 有哈密顿回路。

3.2.1.3 狄拉克定理
如果 $G$ 是一个有 $n$ 个顶点的简单图,其中 $n\geq3$ ,并且每个顶点的度都至少为 $n/2$ 。那么 $G$ 有哈密顿回路。狄拉克定理可以用欧尔定理推导。
3.2.2 必要条件
3.2.2.1 黑白点着色法
黑白两种颜色给图中的点着色,使相邻点的色不同。只有当图中黑白点的个数相等或者相差为1的时候,才说明可能存在哈密顿回路。
3.2.2.2 去边法
考虑哈密顿回路 $C$, 图中每个结点都恰有两条和它关联的边在 $C$ 上。 因此,可以通过对每个结点去掉“多余的边” 得到。如果不能用这种方法得到,说明一定不存在哈密顿回路。
3.2.3 旅行商问题
其实就是求解完全图中总权值最小的哈密顿回路。而完全图中的哈密顿回路有 $(n-1)!$ 条,所以时间复杂度过高,所以是一个NP问题。
中国邮递员问题说的应该是在一个连通图中,寻找一个权值最小的欧拉回路,这道题被中国数学家解决了。
四、树
树之所以重要,是因为它具有非常简单的结构,又具有许多重要的性质。而且大量的图论问题和实际问题最后都可以归结为对树的研究。
4.1 生成树
4.1.1 最小生成树
4.1.2 圈
圈的概念是紧密与生成树联系在一起的。
4.2 有向树与有序树
4.2.1 有向树
4.2.2 有序树
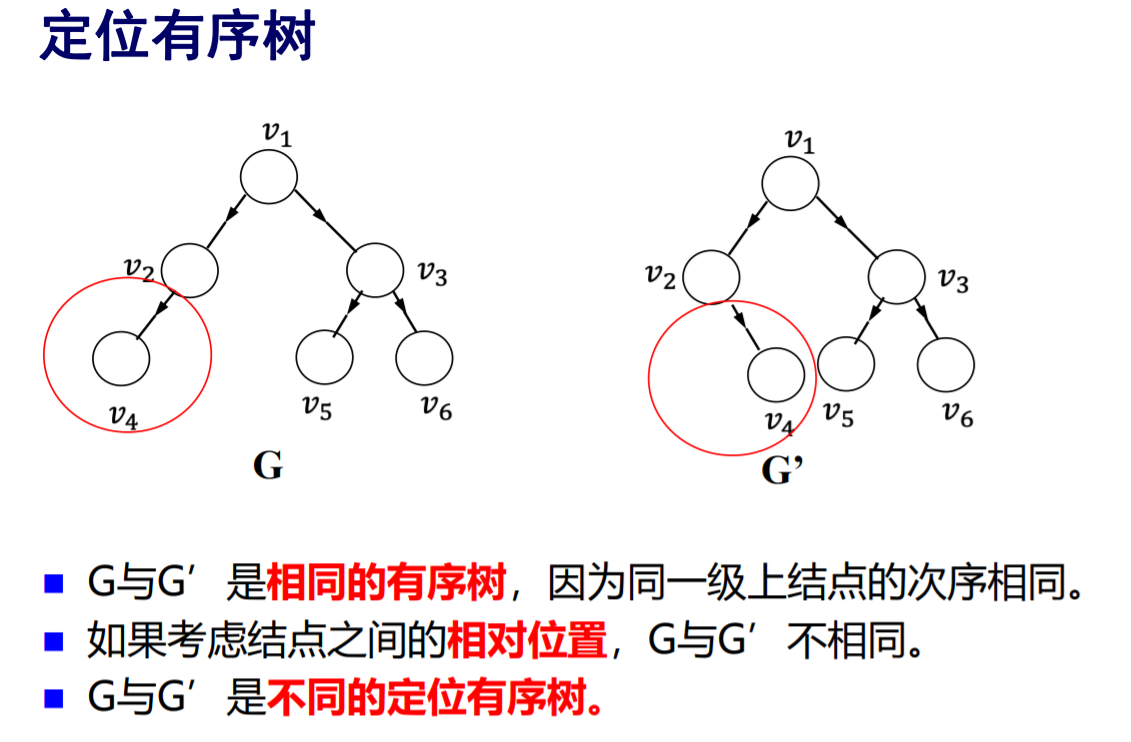
关于有序树和定位有序树的区别,这张图片给出了很好的解释
4.3 二叉树
4.3.1 n 元有向树
出度最大为n。
4.3.2 完全 n 元有向树
出度要么是n,要么是0。完全 n 元有向树又称二叉树。
4.3.3 最优二叉树
Huffman编码。
4.3.4 前缀编码
左0右1.