一、特征方程的求解
这里首先给出一个方程
这个方程描述的是,一个非零向量 $x$ ,经过特定的矩阵 $A$ 进行线性变换,最终的结果是,将 $x$ 拉伸或者压缩自己的实数倍(也就是值改变了向量的长度,没有改变向量的方向)。
这个方程本质上是为了每个特定的 $A$,去寻找一些符合这个条件的 $x$,而 $\mu$ 只是求解的参数,最后求出的解中应该带 $\mu$,但是为了让满足一些非零的条件,我们可以先将 $\mu$ 求出,进而求解每个 $\mu$ 对应的 $x$。
上面的方程可以变形成方程组的形式
因为这个方程组(将上面的式子理解成一个线性方程组)一定有零解,所以如果想要非零解,就说明系数矩阵 $A - \mu I$ 一定是不满秩的,那么就可以用行列式描述这种“不满秩”特性,也就是
这个行列式对应的多项式被称为特征多项式,求出来的值就是特征值 $\lambda$。
然后根据求解出来的 $\lambda$ ,带入原特征方程,就可以求解出特征向量了。
二、特征向量与相似性
2.1 相似定义
设 $A, B$ 是 $n$ 阶方阵,如果存在 $n$ 阶可逆方阵 $P$ ,使得
则称 $A$ 与 $B$ 相似。
如果想要直观理解,可以这样理解同一个线性变化,在不同基下的矩阵,称为相似矩阵。也就是下面的图
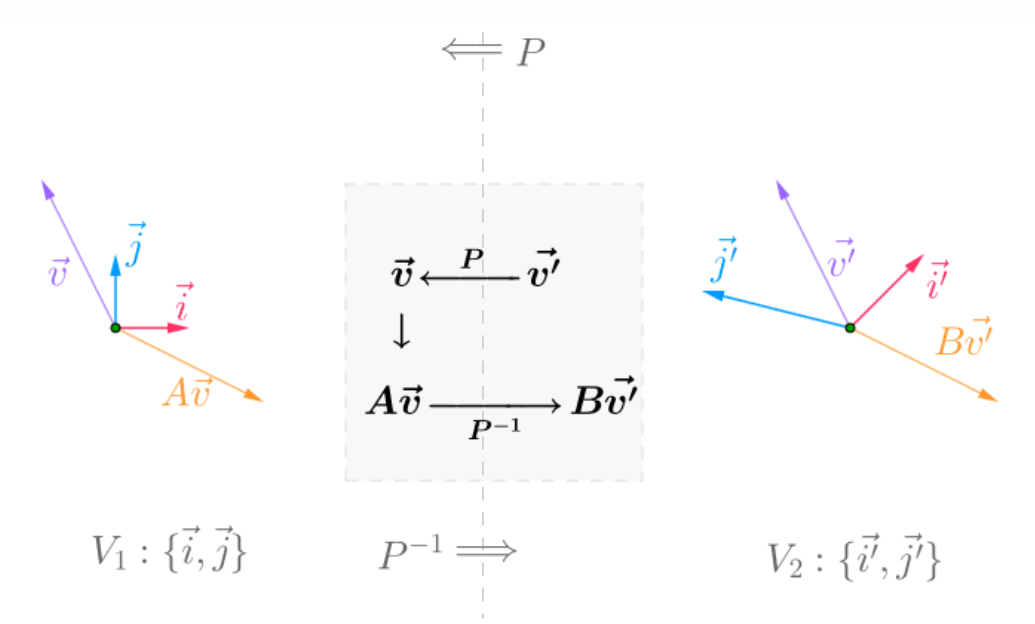
发生的都是线性变换都是将紫色的向量变成黄色的向量,但是因为基的不同,所以线性变换的内容也由 $A$ 变成 $B$。在推导中,有

其中 $P$ 就是由 $V2$ 到 $V1$ 的过渡矩阵(也可能反过来,我没时间探究了)。
2.2 特征向量与对角矩阵相似
我们进行基变换的目的一般都是为了让线性变换的形式更加简单(就好像我们喜欢沿着椭圆的长短轴建系一样),那么线性变换比较简单的一个形式就是对角矩阵,因为在这个形式下,变化变得十分显然。
我们举一个例子来联系特征向量和对角矩阵相似推导。
这个方程的三个特征向量分别是 $X_1 = (1, 0, 0)^T, X_2 = (0, 1, -2)^T, X_3 = (1, -2, 0)^T$ ,分别满足 $AX_1 = 3X_1, AX_2 = 3X_2, AX_3 = -X_3$ ,如果令
那么由特征方程有
如果再令
这个 $D$ 就是由特征值构成的对角矩阵,那么就有
三、矩阵的运动
到底特征值和特征向量怎样用运动去理解,我们知道,当一个方阵A满秩时候,就有
其中
$\alpha_i$ 是特征值 $\lambda_i$ 对应的特征向量。
我们知道,在运动的观点下看,矩阵乘法的意义是把原来的一个向量x通过矩阵A变换成一个新的向量,发生了一次运动,原来我理解特征值和特征向量就是,只有特征向量会在A的作用下方向不发生改变,只有大小发生改变,改变的倍数就是对应特征值,但是这样分析好像不够本质,我们用多次运动来将其更加直观一些。即A次幂,有
其中,$\lambda_1$是最大的特征值,当k趋于无穷的时候,中间的矩阵会变成一个左上角为1,其他所有地方都是0的矩阵,然后先运算 $P^{-1}x$ 将其第一个分量记为c,有
也就是说,无论输入什么向量,在多次运动后,其方向都会趋于最大特征值对应的特征向量的方向,也就是说,这个矩阵有一个很本质的运动趋势可以用特征向量来概括,就好像推动帆船的风一样,虽然船的方向不一定与风相同,但是只要吹得久,最终都会相同。