一、有序和单调
二分本质上是一种更加智能的搜索状态空间的方式,他需要状态空间的状态呈现一种“有序的一维数组”的形式,然后再进行搜索。所以一开始的排序是无法避免的。
因为二分的写法问题,所以应当怎样排序也是有一定讲究的,所以排序的时候就可以定义一定的比较方式。
如果更加细致的讨论的话,其实有序只是一个“小条件”,比如说很多枚举、搜索类的题目的状态空间也是有序的,但是我们却没有用二分法,这是因为其核心是,适用于二分法的题目,它的状态和解之间的关系是单调的,如下所示
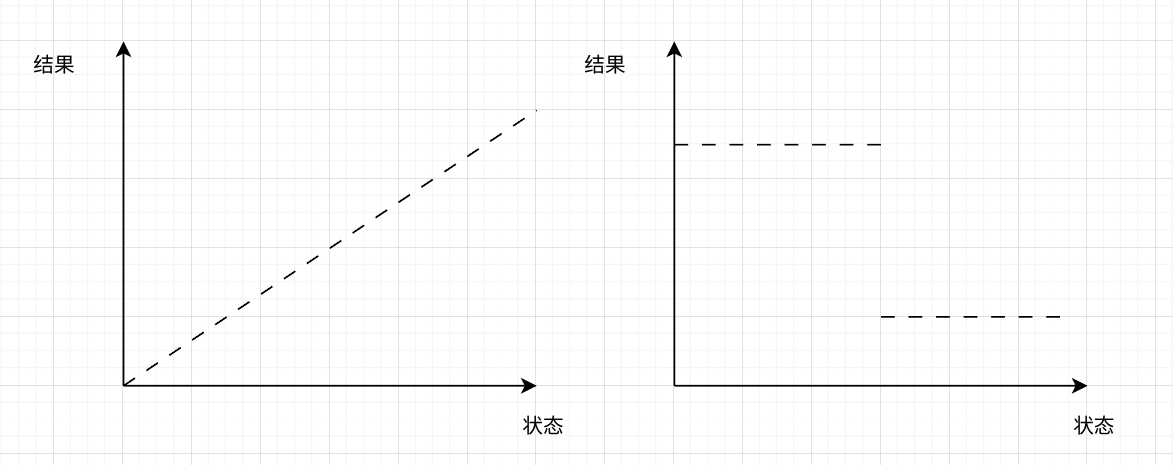
如左图所示,如果我们对于 mid 有了一个讨论,我们就可以根据需求去选择往左或者往右,右图也是同理,我们知道只要小一点就可以将结果置高,那么最终的结果就会变成“到底小多少”,就是一个很容易解决的问题了。
但是如果状态和结果之间的关系并不单调,那么就无法使用二分法了,如下所示
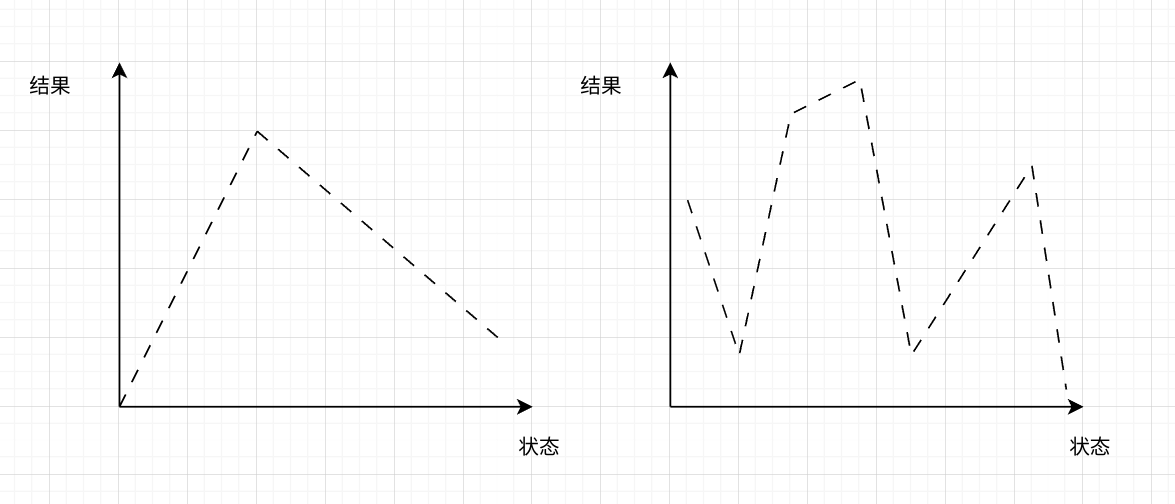
左图还可以使用“三分法”,但是对于右侧,完全没有办法使用“分法”了,但是不可否认,右图的状态空间也是有序的,没准可以用动态规划求解。
二、二分模板
二分一共有两个模板,这是因为二分的本质不是通过二分找到“唯一适合“的点,二分一般呈现一种“最优化”的特点,它要找到是“符合条件”的最大的或者最小的。我们下面的讨论,都默认状态空间是增序排列的。
这就导致当 mid 符合条件的时候,我们需要判定该往哪一边走了,通常情况下,我们希望找到约束条件下的最大值,那么就应当向 mid 右侧去寻找,而当我们希望找到约束条件下的最小值,那么就应当向 mid 的左侧去寻找。
在寻找更小的区间的时候,有两个原则需要遵守,一个是缩小后的区间一定是包括 mid 的,是不可以跳过 mid 的,这是因为 mid 可能是唯一的“最优值”,所以是不能跳过的;另一个是一定要在 mid 的基础上进行移动,比如说 mid + 1, mid - 1 这样的移动,这是因为在整数中,如果 right - left = 1 而不进行移动,也就是 left = mid, right = mid ,这就会导致死循环的出现。综上所述,我们一般在 mid 符合约束条件的时候,利用的是 left = mid, right = mid 来确保对于 mid 的保留,而当 mid 不符合条件的时候,进行 left = mid + 1, right = mid - 1 的操作来避免死循环。
同时,需要注意二分法的边界条件,这个其实有多种写法,我选择了 left < right 作为循环的条件,那么退出的时候就有 left == mid == right,可以选择任何一个索引作为最终结果。
最后,还需要注意当搜索不到的情况,最后会返回什么,这取决于区间缩小时的移动条件,如果是 left = mid + 1,那么就会导致在 right 暂停,相反,则在 left 暂停。
所以模板如下,对于选择“最小值”,其中 check(int) 函数用于检测是否满足条件:
// 求符合约束的最小值
while (left < right)
{
// 向下取整
int mid = (left + right) >> 1;
// mid 是满足条件的,那么向左侧搜索,包括 mid
if (check(mid))
{
right = mid;
}
// mid 不满足条件,向右侧搜索,那么最可能满足条件的是 mid + 1
else
{
left = mid + 1;
}
}对于选择“最大值”
// 求符合约束的最大值
while (left < right)
{
// 向上取整
int mid = (left + right + 1) >> 1;
// 如果 mid 满足条件,那么向右侧搜索,包括 mid
if (check(mid))
{
left = mid;
}
// mid 不满足条件,向左侧搜索,最有可能满足条件的是 mid - 1
else
{
right = mid - 1;
}
}对比如下
| 条目 | 模板 1 | 模板 2 |
|---|---|---|
| 目标 | 求出满足约束的最小值 | 求出满足约束的最大值 |
mid 取整方式 |
向 left 取整 |
向 right 取整 |
| 搜索为空的返回值 | 状态空间 right |
状态空间 left |
| 跳过方向 | 向右 left = mid + 1 |
向左 right = mid - 1 |
三、STL 算法
与上面提出的模板类似的 stl 算法是 lower_bound() ,它可以返回第一个大于等于某个值的迭代器,也就是这个值的下界位置
// 在 [first, last) 区域内查找不小于 val 的元素
ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last,
const T& val);
// 在 [first, last) 区域内查找第一个不符合 comp 规则的元素
ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last,
const T& val, Compare comp);还有一个类似的函数是 upper_bound() ,它可以返回第一个大于某个值的迭代器,也就是这个值的上界位置
// 查找[first, last)区域中第一个大于 val 的元素。
ForwardIterator upper_bound (ForwardIterator first, ForwardIterator last,
const T& val);
// 查找[first, last)区域中第一个不符合 comp 规则的元素
ForwardIterator upper_bound (ForwardIterator first, ForwardIterator last,
const T& val, Compare comp);然后还有一个 equal_range() ,返回的是两个迭代器的 pair,指明了范围
// 找到 [first, last) 范围中所有等于 val 的元素
pair<ForwardIterator,ForwardIterator> equal_range (ForwardIterator first, ForwardIterator last,
const T& val);
// 找到 [first, last) 范围内所有等于 val 的元素
pair<ForwardIterator,ForwardIterator> equal_range (ForwardIterator first, ForwardIterator last,
const T& val, Compare comp);最后还有一个 bin_search() ,返回一个布尔值来确定在有序状态空间中是否有特定值
//查找 [first, last) 区域内是否包含 val
bool binary_search (ForwardIterator first, ForwardIterator last,
const T& val);
//根据 comp 指定的规则,查找 [first, last) 区域内是否包含 val
bool binary_search (ForwardIterator first, ForwardIterator last,
const T& val, Compare comp);示意图如下
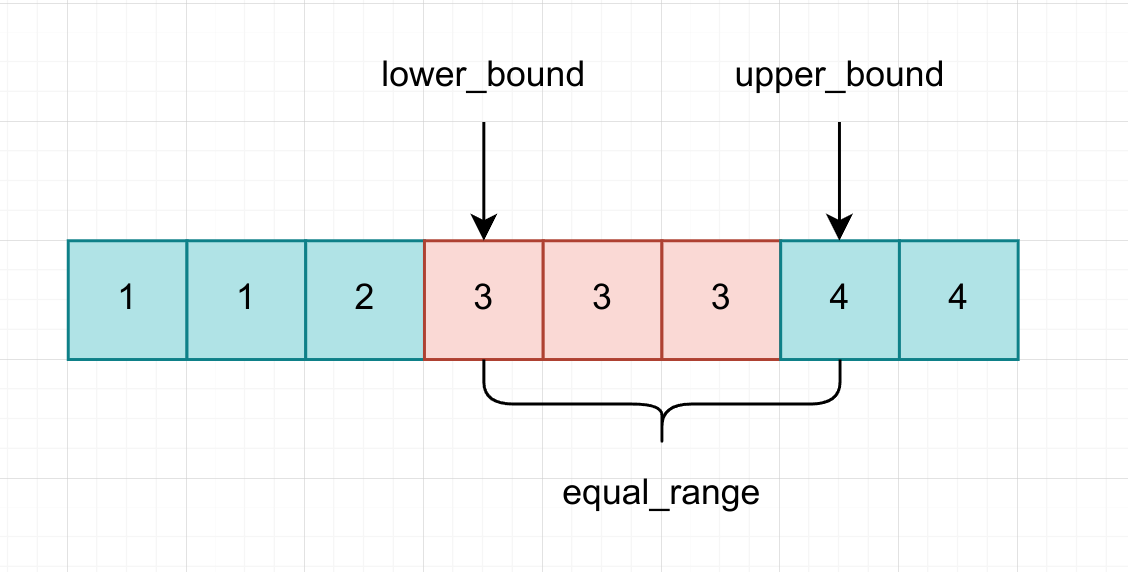
对于 lower_bound() ,其实本质是模板 1 的设计模式,找到的是符合条件的最小值,其代码如下
template <class ForwardIterator, class T> // ForwardIterator 前向迭代器
ForwardIterator lower_bound(ForwardIterator first, ForwardIterator last, const T &val)
{
// it 对应 mid
ForwardIterator it;
// traits 是萃取机的意思,也就是萃取 iterator 里的信息,并给到算法
// count 是搜索区间步长,step 是下一步的步长
iterator_traits<ForwardIterator>::difference_type count, step;
// count 的初始值就是 first 和 last 的距离(first 对应 left,last 对应 right)
count = distance(first, last);
// 步长大于 0,与 left < right 相同
while (count > 0)
{
it = first;
// 二分
step = count / 2;
// 等价于 mid = left + (right - left) / 2
advance(it, step);
// 判断 mid 是否满足条件
// mid 此时不满足条件
if (*it < val) // 或者 if (comp(*it,val)),对应第 2 种语法格式
{
// first = mid + 1
first = ++it;
// count 约缩小一半
count -= step + 1;
}
// mid 满足条件,缩小步长(与使用 last 类似)
else
{
count = step;
}
}
return first;
}因为与模式 1 相似,所以当不存在相似的值的时候,返回的迭代器等于 last 。
upper_bound() 的本质依然是模板 1,因为它寻找的是满足大于搜索值的最小值,所以代码结构与 lower_bound() 相同。
template <class ForwardIterator, class T>
ForwardIterator upper_bound(ForwardIterator first, ForwardIterator last, const T &val)
{
ForwardIterator it;
iterator_traits<ForwardIterator>::difference_type count, step;
count = std::distance(first, last);
while (count > 0)
{
it = first;
step = count / 2;
std::advance(it, step);
// 与 lower_bound() 只有这里不同,此时表示 mid 不满足大于的条件
if (!(val < *it)) // 或者 if (!comp(val,*it)), 对应第二种语法格式
{
first = ++it;
count -= step + 1;
}
else
{
count = step;
}
}
return first;
}同样的,当不存在相似的值的时候,返回的迭代器等于 last 。
equal_range() 本质就是调用了 lower_bound() 和 upper_bound() ,如下所示
template <class ForwardIterator, class T>
pair<ForwardIterator, ForwardIterator> equal_range(ForwardIterator first, ForwardIterator last, const T &val)
{
ForwardIterator it = std::lower_bound(first, last, val);
return std::make_pair(it, std::upper_bound(it, last, val));
}binary_search() 调用了 lower_bound() ,将返回值与 last 比较,并且确定搜索值比最小值(first)小(这是搜索不到的情况)
template <class ForwardIterator, class T>
bool binary_search(ForwardIterator first, ForwardIterator last, const T &val)
{
first = std::lower_bound(first, last, val);
return (first != last && !(val < *first));
}四、二分验证法
这是一类固定的题型,一般呈现“最小最大值”这样的特点(并不绝对),其本质是其答案的状态空间呈现很好的线性有序性(说不定就是个 $[0, max)$ 的区间),我们可以通过二分答案的方法,获得 mid 值,然后利用这个 mid 值去进行模拟验证,如果可以的话,那么就二分继续搜索。
比如说下面的这题
[NOIP2015 提高组] 跳石头
题目描述
这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有 $N$ 块岩石(不含起点和终点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达终点。
为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走 $M$ 块岩石(不能移走起点和终点的岩石)。
输入格式
第一行包含三个整数 $L,N,M$,分别表示起点到终点的距离,起点和终点之间的岩石数,以及组委会至多移走的岩石数。保证 $L \geq 1$ 且 $N \geq M \geq 0$。
接下来 $N$ 行,每行一个整数,第 $i$ 行的整数 $D_i( 0 < D_i < L)$, 表示第 $i$ 块岩石与起点的距离。这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同一个位置。
输出格式
一个整数,即最短跳跃距离的最大值。
样例 #1
样例输入 #1
>25 5 2 >2 >11 >14 >17 >21样例输出 #1
>4提示
输入输出样例 1 说明
将与起点距离为 $2$和 $14$ 的两个岩石移走后,最短的跳跃距离为 $4$(从与起点距离 $17$ 的岩石跳到距离 $21$ 的岩石,或者从距离 $21$ 的岩石跳到终点)。
数据规模与约定
对于 $20\%$的数据,$0 \le M \le N \le 10$。
对于 $50\%$ 的数据,$0 \le M \le N \le 100$。
对于 $100\%$的数据,$0 \le M \le N \le 50000,1 \le L
\le 10^9$。
可以看到这个题目的答案空间是在 $[0, L)$ 之间的,虽然题目看着很复杂,但是如果考虑用二分的方法去做,对于每一个 mid 值的检验,是很容易进行模拟的,如下所示
#include <bits/stdc++.h>
using namespace std;
int l, m, n;
int d[50005];
// 对于传入的 mid,进行模拟检验
bool check(int step)
{
int cnt = 0;
int pre = 0;
for (int i = 0; i <= n; i++)
{
// 如果距离小于 step,说明需要将这个石头移除
if (d[i] - pre < step)
{
cnt++;
}
// 否则就更新前一个木桩
else
{
pre = d[i];
}
}
// 最终的结果是移除的石头不能多余 m
return cnt <= m;
}
int main()
{
cin >> l >> n >> m;
for (int i = 0; i < n; i++)
{
cin >> d[i];
}
d[n] = l;
int left = 0, right = l + 1;
// 因为是求解最大值,所以采用的是模板 2
while (left < right)
{
int mid = (left + right + 1) >> 1;
if (check(mid))
{
left = mid;
}
else
{
right = mid - 1;
}
}
cout << left;
return 0;
}需要注意的是,在 check() 中,因为采用的是模拟方法,所以可能会导致复杂度比较高,所以当模拟到失败的时候,需要进行减枝优化。比如说洛谷上的这道题目 https://www.luogu.com.cn/problem/P3853 ,它的格式基本上与前面的题目相同,但是在 check() 上进行减枝
bool check(int step)
{
int cnt = 0, pre = 0;
for (int i = 0; i < n;)
{
if (d[i] - pre > step)
{
cnt++;
pre += step;
}
else
{
pre = d[i];
i++;
}
// 减枝
if (cnt > m)
{
return false;
}
}
return true;
}五、实数二分
实数二分的模板要更加容易记忆,唯一需要注意的就是精度问题,因为控制不好精度,很容易导致死循环(似乎到了 1e-7 左右就容易 tle,这可能是由于双精度浮点数的精度相比较大导致的,所以一般采用 1e-6),一定要注意题目中的描述,模板如下
double left = 0, right = 1e10;
while (left + 1e-6 < right)
{
double mid = (left + right) / 2;
if (check(mid))
{
left = mid;
}
else
{
right = mid;
}
}