这一章最让我困惑的原因是因为我的几何光学的知识存在欠缺,这个部分是不在授课中出现的,但是确实后面波动光学用到了凸透镜的知识,但是我缺少,就造成了很多的疑问。
另一个比较让人分不清的点,是其实衍射现象的观察实际上利用的是波的叠加原理,也就是光的干涉。这个才是在光栅衍射的时候衍射对干涉调制的原因,如果意识不到这件事情,那么就会有很多理解偏差。
波动光学
一、几何光学的前置知识
几何光学的前置知识主要有两点,第一个一个是一个平面上的平行光透过透镜以后,会汇聚到焦平面上的一点(如果是一个面光源,那么就是一条线)。示意图如下
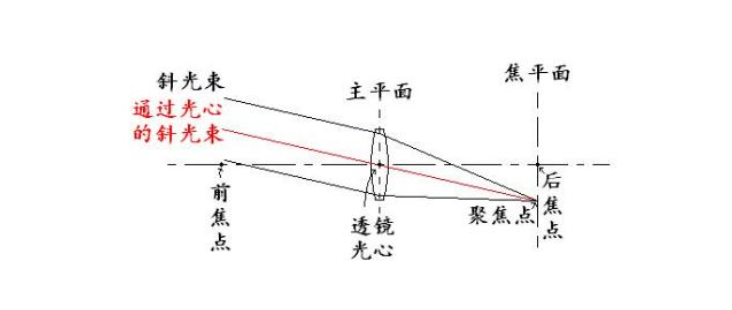
这个知识的作用是在我们进行等倾干涉的时候,本来角度相同的相干光线是没有办法发生干涉的,因为是平行的,我们利用凸透镜,可以将他们汇聚到一点,这样就可以发生干涉了。如果再往深了讲,会发现,当角度固定时,汇聚点的位置是可以确定的,就是
其中,x是汇聚点到后焦点到距离,d是透镜光心到焦平面的距离,$\theta$ 是光束与x轴的夹角。所以说,只要 $\theta$ 是确定的,那么x就是确定的。这也是等倾干涉条纹是环形的原因,因为倾角相同,半径就相同,组成的就是环形条纹。
此外,这个知识在观察衍射的时候也有用到。衍射的光是向各个方向都有的,在各个位置都有,所以透镜可以把在各个位置相同方向的光汇聚到一个点上,这也是衍射条纹的来历,同样,衍射的条纹的位置也与倾角呈函数关系。
另一个知识就是当光透过凸透镜的时候,光程差是不会发生改变的。这个为在实验中添加透镜,而不用考虑透镜的影响提供了理论依据。
二、薄膜干涉
2.1 相干光的产生方法
在薄膜干涉中,利用的是当一束光投射到两种介质的分界面的时候,一部分反射,一部分投射,但是无论怎样,分出的光束的相位都是相同的(或者要考虑半波损失,但是总是是可控的)这样就形成了相干光。随着光能被分成两部分,光的振幅也被分成了两分,所以这个方法称为分振幅法。
还有一种方法叫做分波振面法。这是因为在一个波振面上的相位都相同,所以产生的都是相干光。这个方法在杨氏双缝干涉中用到。
2.2 等倾干涉
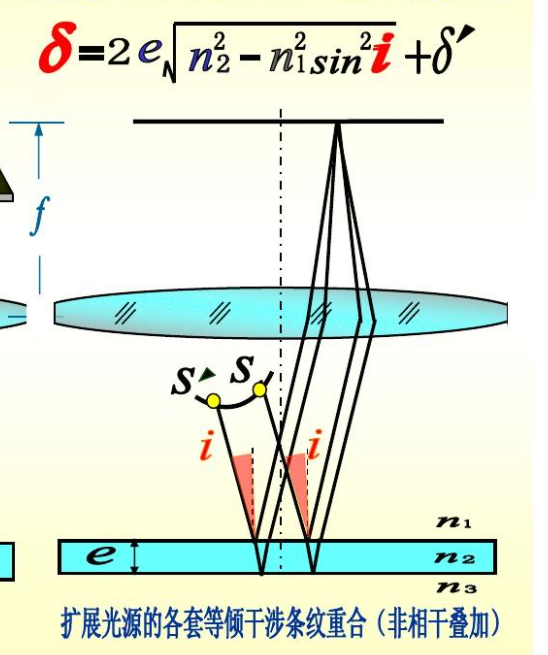
可以看到,等倾干涉产生的原因是其中一束光在薄膜的上表面就发生了反射,而另一束光是原光通过折射进入薄膜,然后折射光再在下表面发生反射,然后再在上表面折射出薄膜,形成的。这两束光的角度是相同的,所以本来是不会汇聚的,但是我们加入了一个凸透镜,所以就可以汇聚平行光了,所有这个角度的光(无论原光是不是同一个),都会被汇聚到焦平面的一点。我们需要计算光程差,有图片中的上式,之所以要多加一个半波长,是因为发生了半波损失(因为在第一束光的反射是光疏到光密,但是第二束光的反射是光密到光疏)。
上面讨论的是反射光发生的干涉,其实透射光也会发生干涉
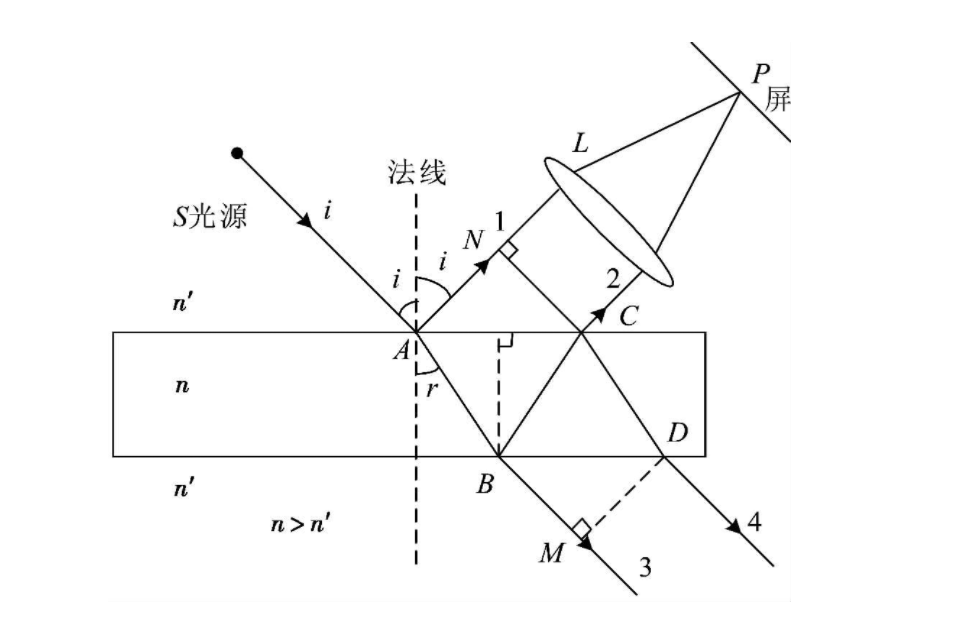
12是反射光,34是透射光,但是透射光是没有半波损失的。所以透射光明纹的条件刚好是反射光暗纹的条件,反之也成立。这说明干涉现象引起了光能的重新分布。
我们在实际应用的时候,会发现 i 这个角度是很小的(即垂直入射)。所以计算反射光暗纹式子就退化成了这样。当反射光为暗纹的时候,就说明反射光相消了(这个不需要透镜也能做到,这是因为是一个面光源,透镜没有造成干涉,他只是让干涉现象可以为人观测,他改变了干涉的状态)
所以我们的增透膜,就是让膜的厚度d取 $\frac{\lambda}{4n} $ 这样就可以达到增透的效果(也可以换个角度理解,就是透射光在这个厚度下会相互叠加(类似明纹),这样透射光就强了)
2.3 等厚干涉
等倾干涉的名字是说,只要倾角相同,那么光程差就是相同的,等厚干涉说的是,只要厚度相同,那么光程差就是相同的
空气劈尖等厚在说的时候强调了光线要垂直于倾面,但是实际是做不到的,因为倾面倾角是未知的,要是能垂直,那还用这个方法测啥倾角。所以肯定不是垂直的,所以一定会发生等倾干涉,但是只要不加透镜,等倾干涉就是没有办法被观测到的(会出现相干光,但是不会汇聚到一点),所以就不考虑了。示意图如下:
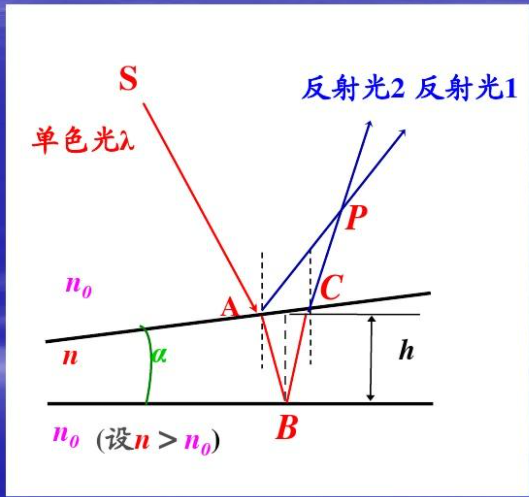
这也是会发生半波损失的。所以相应的公式计算光程差
2.4 迈克尔逊干涉仪
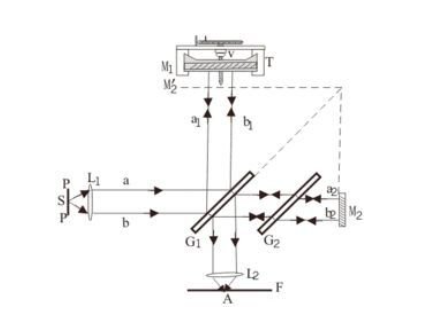
其中G1被称为分光板,是因为平行光经过G1,有的被反射,那么就向上走,有的发生透射,那么就向右走,这两种光经过反射,最终发生了干涉。G2被称为补偿板,是因为反射光会穿过玻璃板三次,而透射光只会穿过玻璃板一次(要是没有G2),所以为了弥补光程差,所以增加了G2。
之所以选择这个图,不是因为这个图直观,实际上这个图非常的不直观,之所以选择这个图,是因为在目镜侧,他画了一个凸透镜,这正是其他图没有的。
我们知道,迈克尔逊干涉仪不仅可以用来观测等倾干涉,还可以用来观测等厚干涉。据说只需要把M2调成不水平的就好了,但是我觉得,就像在等厚干涉这一章中说的,必须把凸透镜去掉,才可以观察得到,不然没办法想象条纹是怎样由等倾的环形变成等厚的条形。
三、衍射
3.1 单缝的夫琅禾费衍射
首先要明确的是,衍射说的是啥事情
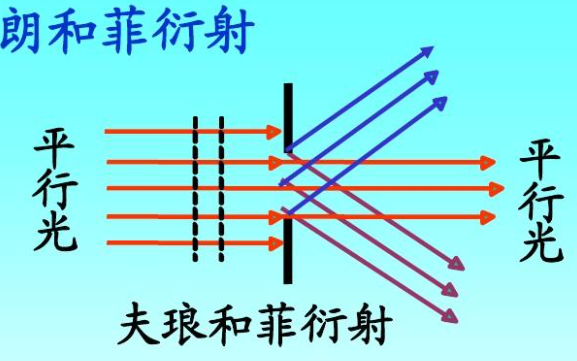
就是说本来平行于x轴的光,经过一个小孔以后,方向变得五花八门的了,往哪里走的都有。但是需要注意的是,尽管往哪个方向走的都有,但是不是每个方向都均分光的能量,我们在后面的计算中可以看到,中央明纹(也被称为主极大)的光强远远超过了其他方向。
但是仅仅是这种现象,我们是观测不到的,所以还是用处理等倾干涉的方法,加一个透镜,这样向一个方向发射的光,就会被汇聚到一个点,也就是这样
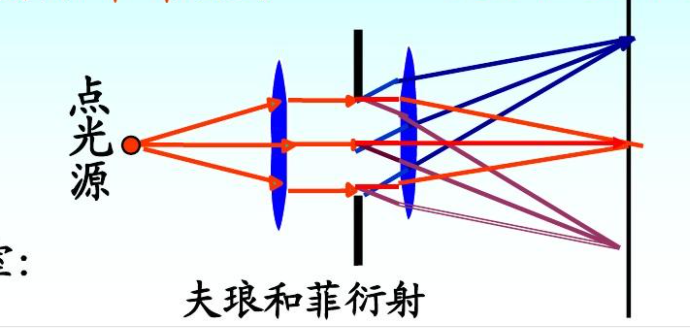
也跟在第一章论证的一样,条纹的距离与角度之间呈现了函数关系,我们就可以对此进行研究了。
另外还是需要强调,这里虽然是衍射,但是这种把相同的光汇聚到一起,然后发生光的叠加的设计思想,利用的其实是光的干涉。也就是说,我们虽然研究的是衍射,但是是利用干涉在研究衍射(衍射就是那个原本沿直线传播的光突然哪个方向传播都有了这件事)。
3.2 单缝衍射的一些公式
我们计算单缝衍射的时候,其实最本质的是用惠更斯-菲涅尔原理,但是因为数学计算比较麻烦,所以我们想了两种替代的方法,一个是菲涅尔半波带法,一个是矢量振幅法。
对于菲涅尔半波带法,我们有这样的原理图
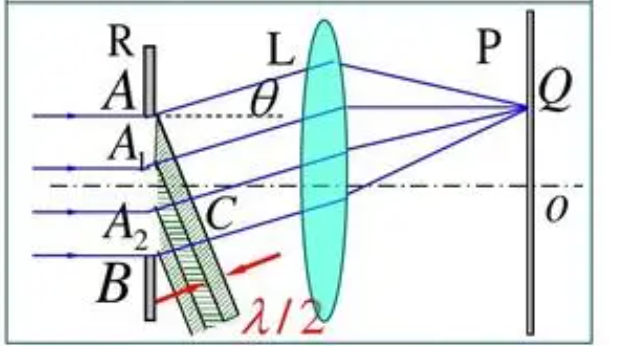
大致意思就是说,按照半波长的方法(被分割的宽度乘上角度正弦等于半波长)对狭缝进行分割,相邻的光会抵消(相差半波长),最后只剩下来一个分剩下没抵消的(那么就会出现明纹),或者一个都没剩(就会出现暗纹)。
所以最后会有式子,其中d是单缝的宽度
这个是暗纹出现的条件,用于求解 $\theta$ ,有了 $\theta$ 就可以求解暗纹位置了,在暗纹之间的就是明纹(好像只对中央明纹成立),所以中央明纹的范围是
其他明纹的位置
也是很好理解的。
此外,当 $\theta$ 增大的时候,会发现被分割的宽度减小了,那么最后剩下的那一个分割的宽度也就减小了,宽度小了,强度就弱了(惠更斯-菲涅尔原理),所以也可以从这个角度理解远离中心的亮纹很弱这件事情。
关于衍射的图样,应该有如下称呼,中央明纹,也就是最亮的那个,同时也叫做零级明纹,它两侧的,叫做一级暗纹,零级明纹和一级暗纹共同组成了第一级光谱线。在两个一级暗纹外的两纹,才是一级亮纹。依次类推。
3.3 圆孔衍射
之前提到的衍射准确的来说的是单缝衍射,所以还有一种衍射叫做圆孔衍射,但是可以看出两者的形式还是一致的。第一级暗环的衍射角,这个角对应形成暗纹围住的亮斑,被称为艾里斑。
对比单缝衍射的第一暗纹公式
可以看到,相差的只是一个常数,形式保持一致。
如果一个点光源的衍射图样的中央最亮处刚好与另一个点光源的衍射图样的第一个最暗处重合,人眼就能够判断出这是两个光点的像。我们说这两个点光源恰好为这一光学仪器所分辨,这一条件称为瑞利判据。简单说,两点光源在透镜处张成的角的大于艾里斑的角的时候,就是可以分辨的
最小分辨角当然越小越好,所以要么增加光学仪器的孔径,要么减少波长(电子显微镜)。
3.4 双缝干涉
为什么双缝干涉要在这里讲呢?是因为产生双缝干涉,其实是衍射现象,我们看原理图
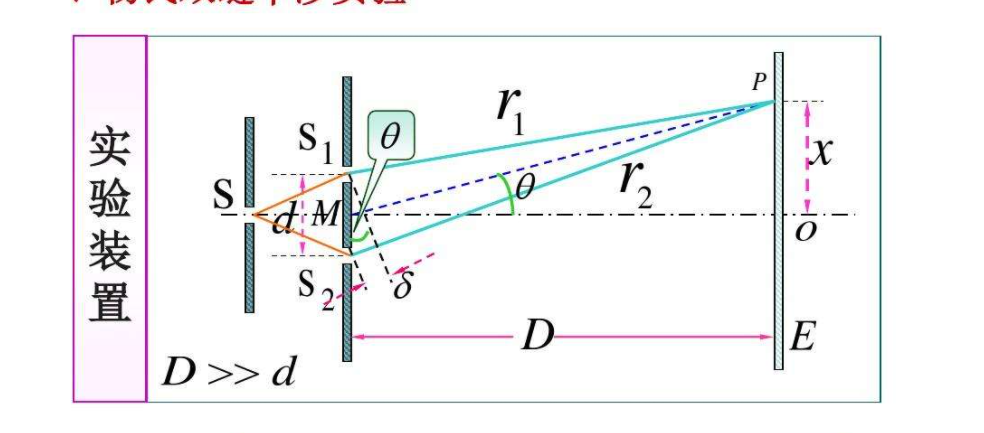
其光程差是
这个式子出现很多遍了,可以说是一个很经典的造成光程差的因素了。
会发现原来沿x轴正方向传播的平行光,经过双缝以后变得往哪个方向的都有了,所以这其实是一种衍射现象,当然光的叠加部分肯定是干涉。有公式计算各级明纹中心离P0的距离。有一点有意思的事:中间的明纹叫做零级明纹,而不是一级明纹。
其中d是双缝的间距。可以看到,角度是个很重要的光学物理量。
在讲光栅衍射的时候,会讲到衍射对干涉条纹的调制(也就是说,射向不同方向的光的光强是不同的,所以),但是因为双缝干涉中缝宽很小,所以中央亮区的衍展范围很大(简单的公式计算),所以干涉条纹近等于等强度分布。
3.5 光栅衍射
3.5.1 光栅衍射原理
光栅的衍射条纹是单缝衍射和多缝干涉的综合效果。
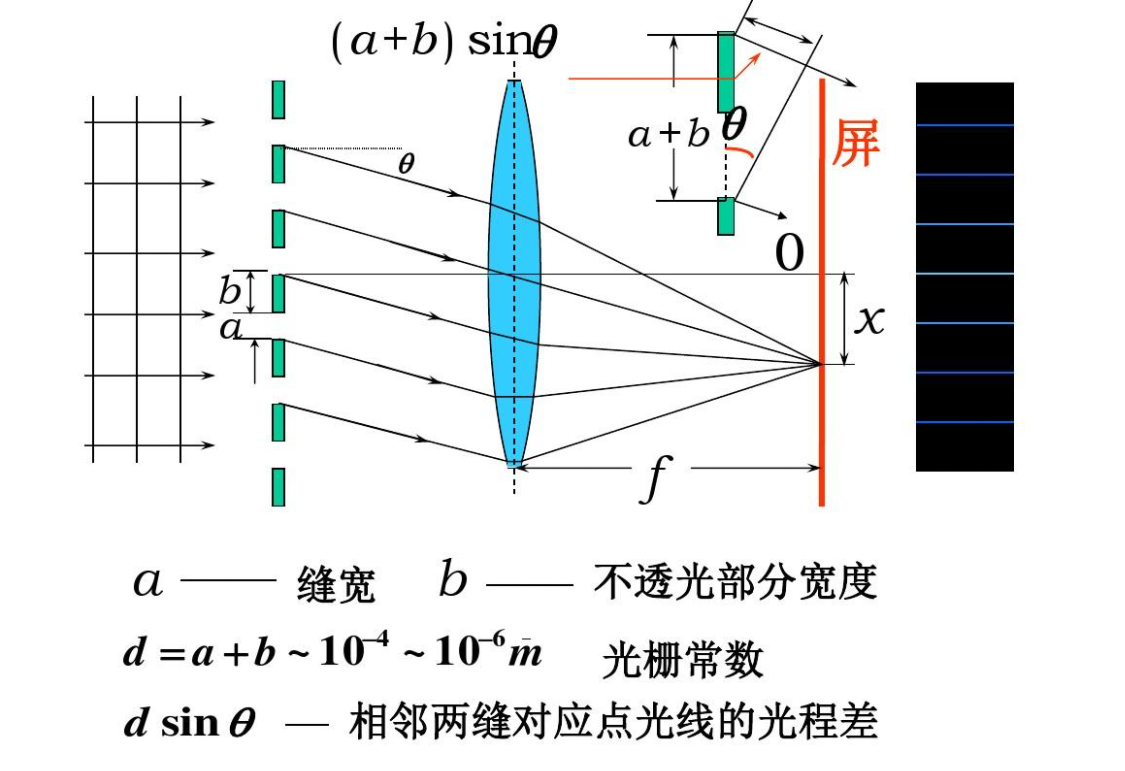
3.5.2 缺级现象
首先分析干涉情况,光栅任意相邻的两缝发出的光到达汇聚点时的光程差都是相等的,所以只要其光程差是入射光波长 $\lambda$ 的整数倍,就会叠加形成亮纹,也就是满足方程(光栅方程)
再考虑衍射情况,不是所有的角度汇聚到一起都有光,可能会出现衍射汇聚时的暗纹,也就是满足
考虑到衍射对干涉的调制,就会出现缺级的现象,也就是同时满足上面两个方程,可以解得
那么当主极大在 $n,2n,3n,\cdots$ 级均不出现的时候,就有
注意,上面这种方法假定 $n$ 是一个正整数,而实际上可能不是,所以这只是一个必要条件,而不是充分条件,也就顶多在选填中使用一下,到了大题,还是需要老老实实的写步骤的。
3.5.3 光栅的分辨率
具体的推导不会,最后记一个公式
其中 $N$ 是光栅的缝数,$k$ 是光谱的级数,$\Delta \lambda$ 是两条谱线的波长差,$R$ 是定义出来的光栅的色分辨本领。
四、偏振
4.1 一些概念
线偏振光(平面偏振光):光矢量始终沿着某一方向振动
圆偏振光(椭圆偏振光):光矢量绕着传播方向旋转,其旋转角速度等于光的角频率,光矢量端点轨迹是圆/椭圆
部分偏振光:自然光相互垂直的独立振动分量不相等(线偏振光是只有一个)
起偏:从自然光中获得偏振光的过程
检偏:检验光是不是偏振光
4.2 马吕斯定律
$\alpha$ 是检偏器的偏振化方向和入射线偏振光的光矢量振动方向之间的夹角。
4.3 布儒斯特定理
自然光在两种介质的分界面是上反射和折射时,反射光和折射光都将成为部分偏振光,在特定情况下,反射光有可能成为完全偏振光。这种情况就是反射光和折射光相互垂直的时候
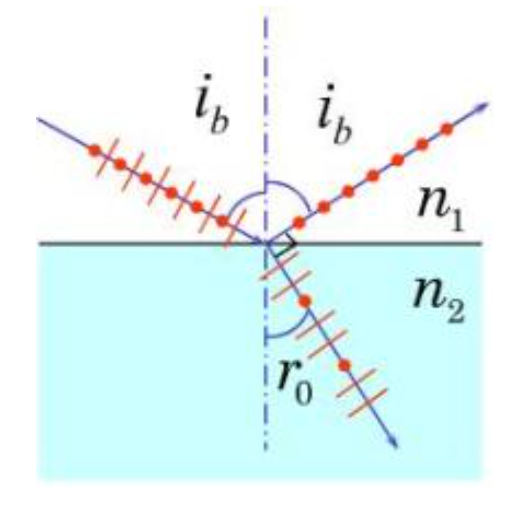
所以有公式(布儒斯特定理)
$i_b$ 也被称为布儒斯特角。
但是依然存在一个问题,玻璃毕竟是一个透光性很强的物质,经过一次反射得到的光,其光强是很弱的,所以我们一般用多个玻璃叠在一起,这样反射光会变强。如图
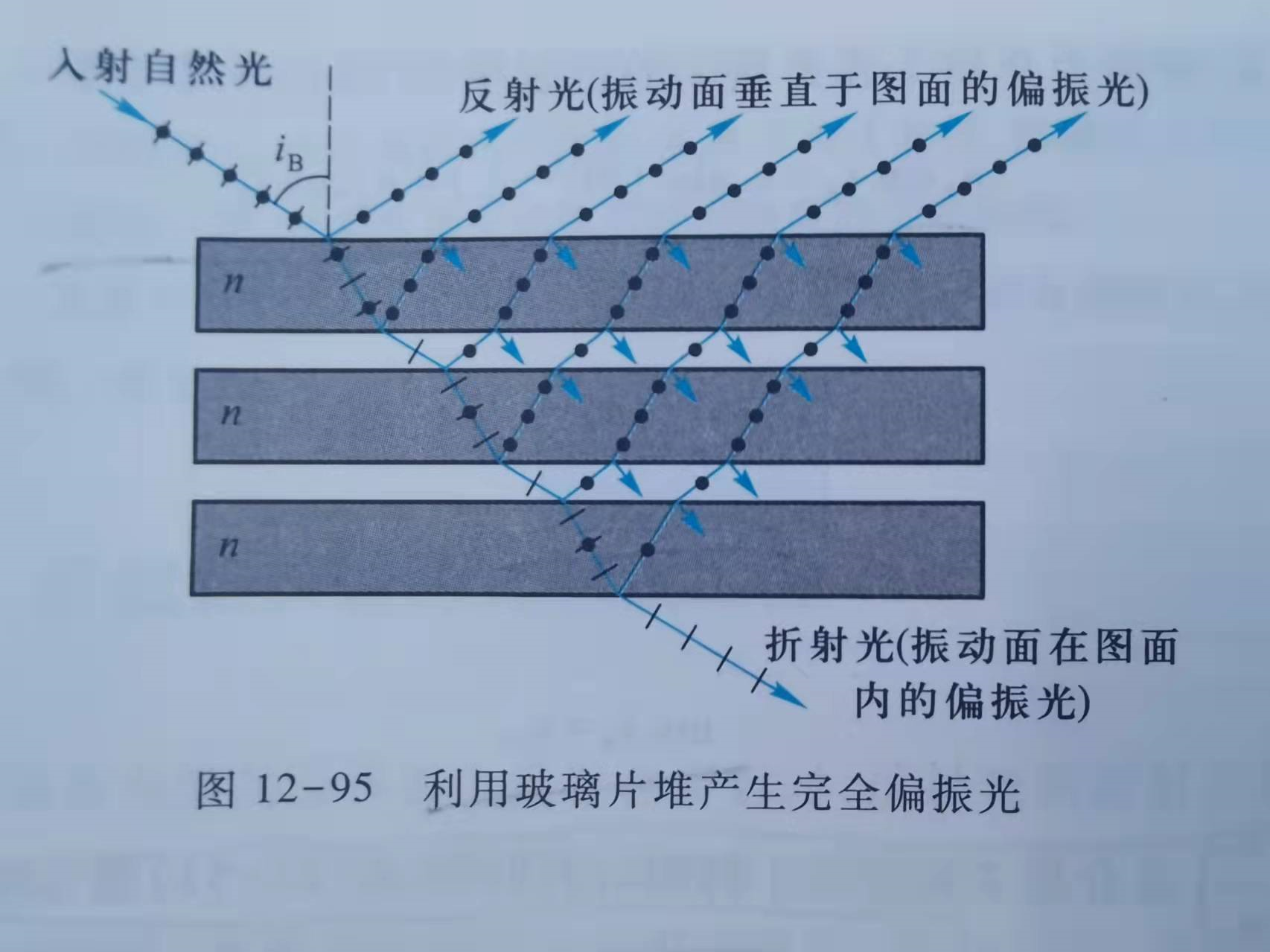
有意思的是,如果考虑由玻璃射向空气得到的发射光,也是偏振光,这是因为有入射角 $r$
满足布儒斯特定理。
五、光的双折射
晶体的各向异性有可能造成双折射。两束折射光之一恒遵守折射定理,称为寻常光(i),另一束光的入射角的正弦与折射角的正弦之比不是衡量,称为非常光(e)。
光沿某一方向传播时,寻常光和非常光不在分开,不产生双折射现象,这一方向称为晶体的光轴。