斯特林数感觉已经偏向于动态规划求解了,是一个很漂亮的组合数学,本来这一部分应该关于生成函数的介绍,但是因为没时间了,所以就鸽了。
在这个博文里,不仅介绍斯特林数,还介绍了对组合数学的一种普遍处理。所以还是有很好的参考意义的。
一、第二类斯特林数
第二类斯特林数记作 $S(n, m)$,意思是把含有n个元素的集合秩为m的划分的个数,如果更加形象一点,就是把n个球丢入m个不加区分的盒子里,并且每个盒子不能为空的方法数。
这个是可以用容斥原理求出通项的,容斥原理是为了计算一个并集中元素的多少,每个组成并集的集合有一条性质来描述,不同的性质之间可能会重合(也就是集合的交不为空集),但是容斥原理可以在重合的条件下很好的计算出元素的个数(也就是这些元素可以满足其中的至少一条性质)。当我们应用容斥原理的时候,有两种用法:一种是求并集性质,也就是所有性质都要满足,这个其实比较反人类,因为一般性质越复杂,计数越简单,所以通常不予考虑(但是这是公式的描述)。另一种是求交集的性质,那么就是在等式两端移项了。
对于这道题来说,我们用的是广义容斥原理(我其实也不知道是不是),我们写个公式
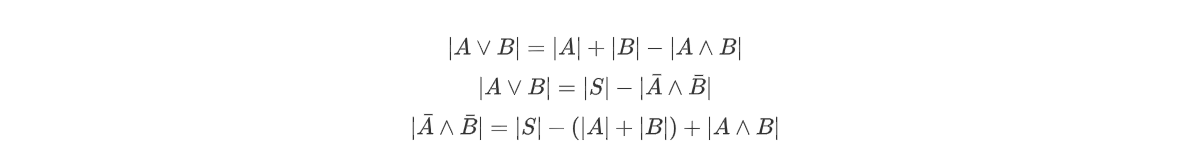
也就是说,我们思考的问题由0个盒子没有被放满,转换为求解至少一个盒子没被放满,至少两个盒子没被放满,至少三个盒子没被放满……
我们可以这样思考,这个数,就是n个球,扔进m个有区分的盒子里的数量(全集数量),减去“n个球,扔进m-1个有区分的盒子里(至少1个盒子中没有球)”的数量,加上“n个球,扔进m-2个有区分的盒子里(至少2个盒子没有球)”的数量,写成通项,就是
然后对他们进行累加,得到
但是因为这样是有标志的盒子,所以要除以组合数,最后得到通项
二、递推与Pascal三角形
除了通项,我们还可以求递推式,这个很好思考,对于 $S(n+1,m)$而言,新加入的球,要么放进原来没有球的盒子(就是新开一个盒子),那么有 $S(n,m-1)$种方法,要么就是放到原来已经有球的盒子中,那么共有m个盒子供其挑选,就是 $m*S(n,m)$ 种方法,所以有状态转移方程
有了状态转移方程,还需要确定一下边界条件,有 $S(n,0) = n^0,S(n,n) = 1$(我不知道当n是0的时候为啥这样),然后就可以递推了。
对于Pascal三角形,也就是杨辉三角,我们熟悉组合数的三角形,这是因为组合数有递推性质
其实Pascal三角形就是适用于所有在(n+1, m)(底),(n, m - 1)(左肩), (n, m)(右肩)间建立关系的递推式。
故其三角形为

三、贝尔数
贝尔数是元素为n的集合的能形成划分的总数目,不难想,贝尔数就是对第二类斯特林数的求和,有
贝尔数也是有自己的递推公式的,考虑 $B(n+1)$ 第n+1个元素如果自己单独形成一个划分,那么就有 $B(n)$ 种,如果第n+1个元素去加入之前含有1个元素的类,那么就有 $C_n^{1}B(n-1)$ 种分法,那么如果加入之前含有2个元素的类,那么就有 $C_n^2B(n-2)$种方法,故有递推式