大学物理-热力学

热力学仅从能量观念出发，研究热力学系统状态变化中热功转换（两种过程能量）的关系与条件。

热力学定律的意义

• 第零定律：热平衡定律，定义了温度的概念。
• 第一定律：包括热现象在内的能量守恒与转化（转化的思想容易被忽视）定律，指明了热力学过程中热功转化之间的数量关系。
• 第二定律：熵增定律，指明了热力学过程进行的方向与条件。
• 第三定律：指明绝对零度不可到达。

一、热力学第一定律

1.1 定律内容

热力学第一定律写作：

$$Q = \Delta E + \int^{V_2}_{V1}pdV$$

这里需要有以下几点解释：第一，Q如果是正的，那么就是系统吸热，反之，则是系统放热。第二、做功A如果是正的，那么是系统对外做功，反之，则是系统被做功，与Q是相反的，之所以写成这样，是因为这是一个由1到2的过程。第三，只有E是一个状态函数（$Q，\Delta E$ 都是与过程息息相关），他是一个状态函数的原因是他是温度的单值函数，而温度是一个状态量，有以下关系：

$$E_0 =\frac i 2 RT$$

但是需要注意的时，在这一节中，还有一个公式写成

$$E_0 =C_{V,m}T$$

上面两个式子其实是一个式子，因为有 $C_{V,,m} = \frac{i}{2}R$ 。正因为如此，下面这个本来由等体过程推导出来的式子，可以用来计算任何过程的 $\Delta E$ 。这本质是因为这是一个状态函数，才有了这种神奇的性质。

1.2 公式计算

在热力学第一定律的公式中，可以看出 $\Delta E$ 的计算相对固定（也就是利用温度进行计算），而Q是没有其他公式可以与之关联的，所以要计算Q，就要算 $\Delta E$ 和做功A，那么A又是积分，所以总的来说，就是在处理A的积分，同时，A的积分还对应了p-v图的面积，正负由起始与终止描述。对于A的描述，我们一般会获得一个过程方程，这个过程方程在p-v图上对应一条线，气体状态就沿这条线变化，这个方程一般作为解题的重要条件。

我们在具体处理的时候，因为有理想气体状态方程，所以我们经常进行换元积分。

1.3 热功转换

我平时很喜欢从右往左看这个公式，就是说将内能和功视为因，吸放热视为果，这其实是不对的，这个公式写成这个样子（我说的其他样子是通过移项得到的），是因为它描述的是热机。左侧是因，右侧是果。

热机的意思是将热量转化成功的机器。热机吸收热量，但是却不能完全转化为对外作功，这是因为有一部分热量被用来使热机自身的温度升高了，这就是这个公式的意思，它指出了吸收的热量的两个去处。用这个角度理解，就可以明确的知道正负的含义了。

在系统状态变化的过程中，功与热的转化不可能是直接的，而是通过物质系统来完成的。向系统传递热量可使系统的内能增加，再由系统内能减少对外做功；或者外界对系统做功，使系统内能增加，再由内能减少，系统对外界传递能量。

所谓的第一类永动机说的就是如果 $Q = 0$ 的情况下，依然可以对外做功，这显然是不可能的。

---

二、准静态过程

2.1 等体过程

等体过程的意思就是吸收的热量全部转化为内能，而不对外做功，有

$$\delta Q = \frac{m}{M}C_{V,m}dT$$ $$C_{V,m} = \frac{i}{2}R$$

其中 $C_{V,m}$ 是定容热容，角标的 $V$ 表示是等体过程，而 $m$ 表示是 1 $molor$ .

2.2 等压过程

等压过程的意思是吸收的热量不仅转化为热能，而且还有一部分转化为对外做功，不仅转化为对外做功，而且还是以等压的形式对外做功。这就表示做功的积分求法很容易。

有迈耶公式

$$C_{p,m} = C_{V,m} + R = \frac{i+2}{2}R$$

再引入绝热系数的概念：

$$\gamma = \frac{i+2}{i}$$

2.3 等温过程

有做功

$$A = \frac{m}{M}RTln\frac{V_2}{V_1}=\frac{m}{M}RTln\frac{p_1}{p_2}$$

这里回顾一下，对于一个指定气体的状态，有三个状态变量，只要知道了其中的两个，确定整个状态。

这其实就是个双曲线积分，过程函数与状态曲线重合了。

2.4 绝热过程

有重要过程方程

$$pV^\gamma =const$$

这个公式不太好推导，所以最好记住，这是一条比等温线更加陡峭的曲线。关于这个结论，有如下推导。首先推导等温线的斜率，有

$$pV = C_1,\quad \frac{dp}{dV} = -\frac{C_1}{V^2} = -\frac{pV}{V^2} = -\frac{p}{V}$$

然后推导绝热线的斜率

$$pV^{\gamma} = C_2,\quad \frac{dp}{dV} = -\gamma\frac{C_2}{V^{\gamma+1}} = -\gamma\frac{p}{V}$$

可以看出，绝热线的斜率更大。

当我们有了这个式子以后，在结合理想气体状态方程，可以推导出其他的等式

$$pV = \frac{m}{M}RT$$

上下两式直接做比，就可以得到

$$TV^{\gamma-1} = const^\prime$$

其他等式推导类似。

2.5 多方过程

介绍多方过程主要是为了引出一个重要的二级结论：“绝热线是区分吸放热的界限，在足够短的一段过程中，在绝热线以下的简单过程（即没有圆之类的）是放热的，在绝热线以上的简单过程是吸热的。（图里写反了）”。如果用图像表示，即

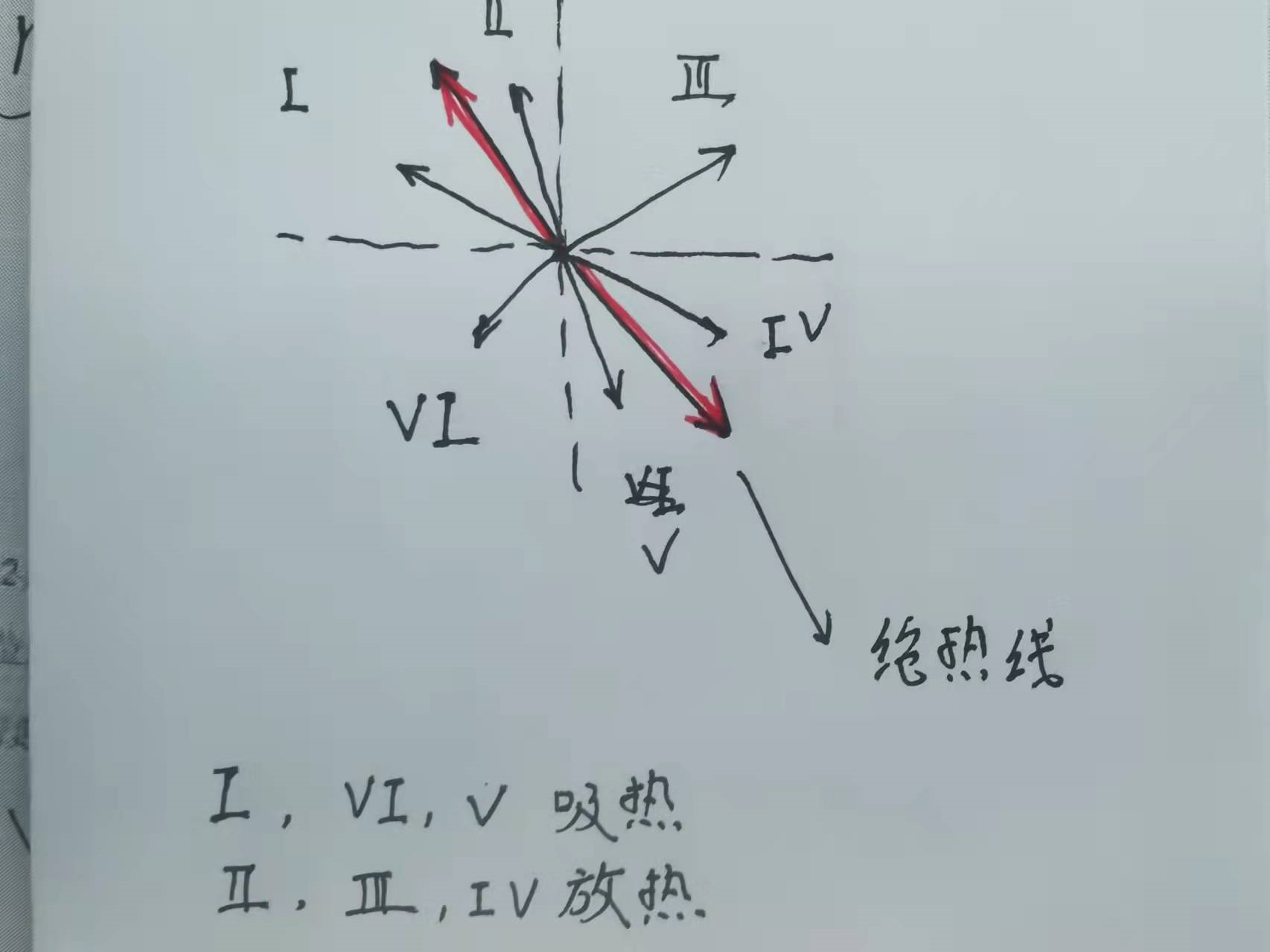
关于这个定理的证明，需要用到多方过程的结论。

多方过程描述的是一小段足够短的过程，他可以用方程来描述

$$pV^{n} = const$$

其在 $(p,V)$ 处的斜率是 $n\frac{p}{V}$。

其中 $n$ 被称为多方指数，然后我们有它的摩尔热容是（已知定理）

$$C_{n,m} = C_{V,m} + \frac{R}{1 - n}$$

显然，如果这个值是个正数，那么就是吸热，反之，则是放热，讨论 $V$ 区域，可以看到 $V$ 区域的斜率要大于绝热线，所以有 $n>\frac{i+2}{i}$ ，那么可以知道

$$C_{n,m} = C_{V,m} + \frac{R}{1 - n} > C_{V.m} - \frac{i}{2}R = 0$$

升高温度需要吸热，而 $V$ 区域变化是像下降温度去的，所以是放热。

---

三、循环过程

3.1 循化过程

一个热力学系统从某一个状态出发，经过一系列变化过程，最后又回到了初始状态。这样的一个过程称为循环过程。

系统沿闭合曲线顺时针方向的循化称为正循环，做正循环的设备叫做热机，它从高温热源吸收热量，对外做功并且对低温热源放热。系统沿闭合曲线逆时针方向的循环称为逆循环，做逆循环的设备叫做制冷机，他从低温热源吸收热量，外界对其做功，最终对高温热源放热。

循环过程的一个特征是系统经历一个循环后内能不变，也就是说，系统吸收的净热量等于系统对外所做的净功。有

$$\Delta E = 0,\quad Q = A$$

3.2 热机与制冷机

对于热机来说，要从高温热源吸收热量，这个热量会转化为向低温热源传递的热量和对外做的功。所以有等式

$$Q_1 = A + Q_2$$

那么热机效率应该看的是热能比值，即

$$\eta=\frac{A}{Q_1} = \frac{Q_1 - Q_2}{Q_1} = 1 - \frac{Q_2}{Q_1}$$

对于制冷剂而言，要对制冷剂做功，使其能够从低温热源吸收热量 $Q_2$ ，并将热量传导给高温热源 $Q_1$ ，所以有等式

$$Q_2 + A = Q_1$$

对于效率，人们一点也不关心垃圾桶（在热机中是低温热源，制冷机是高温热源）。人们只关心自己的投入和产出，所有的效率都是产出比投入。对于制冷系数，有

$$\omega=\frac{Q_2}{A} = \frac{Q_2}{Q_1 - Q_2}$$

3.3 卡诺循环

卡诺循环是一种具有最高效率的理想循环。他的循环如图

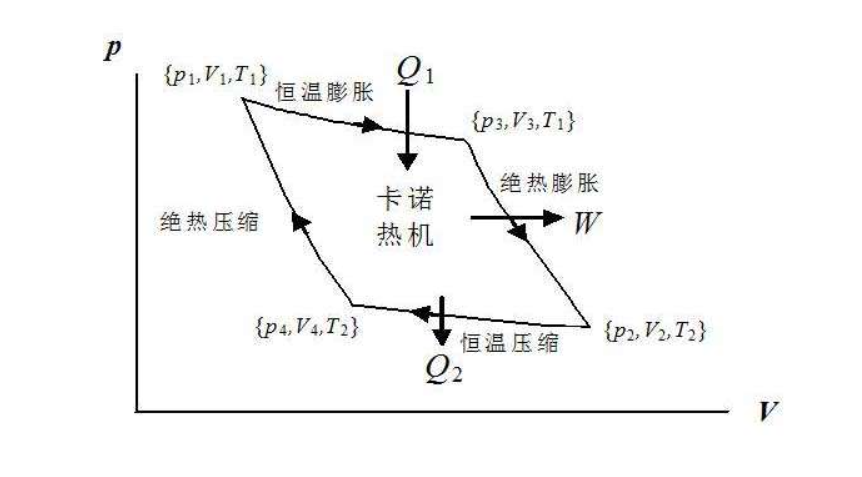
我们先来直观的感受一下他为啥是最高效的，我将热机分为两个功能，一个是工作：在高温热源处的吸热膨胀或者在低温热源处的放热收缩，这是热机的本职工作，另一个是衔接：也就是说，热质在工作的时候会有一个温度的变化，那么就需要一个过程来完成从高温到低温，再由一个过程完成由低温到高温。

对于工作的过程，肯定是等温过程最好，这是因为只有等温过程吸收的热量全部转换为了功，而不会使内能增加。对于衔接过程，肯定是绝热过程最好，因为绝热过程保证了热量不会逸散，也就是说，由于温度下降导致的内能减少，全部用作了对外做功。以奥托循环（现实热机循环）做比

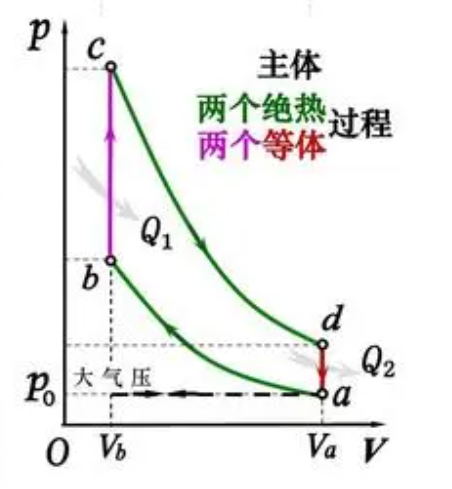
因为用的是等压过程，所以一部分的内能转换为热能，就有所损失。

在卡诺循环中，经过复杂的推导（所以就不列了）有恒等关系

$$\frac{Q_1}{T_1} = \frac{Q_2}{T_2}$$

这其实也是可逆过程的熵恒等。

---

四、热力学第二定律

4.1 热力学第二定律

一切与热现象有关的实际宏观过程都是不可逆的。

有一个有意思的表述：两条绝热线不能相交。因为这样就可以让两条绝热线，一条等温线构成一个循环，这样热机的效率就是 100% 了。

4.2 卡诺定理

• 在同样的高低温热源之间工作的一切可逆机，其效率都是 $1 - \frac{T_2}{T_2}$。
• 在同样的高低温热源之间工作的一切不可逆机，效率不可能高于可逆机。

4.3 可逆过程与熵

设存在一个过程，使物体从状态 A 变为状态 B，对它来说，如果存在另一个过程，它不仅使物体反向变化，从状态 B 变为状态 A，而且当物体回到状态 A 的时候，周围的一切各自恢复到原状，则从状态 A 进行到状态 B 的过程是一个可逆过程。

需要注意的是，可逆只是过程的一种性质，可逆过程不需要一定是一个循环过程。

只有非常缓慢的亦即准静态的膨胀/压缩过程，才是可逆的膨胀/压缩过程。所有的宏观热现象都是不可逆的。

对于熵，我们有这样的一种算法

$$S_2 - S_1 = \int^2_1(\frac{\delta Q}{T})_{可逆}$$

其中 $\delta Q$ 是在各无限短的过程中吸收的微小热量。有趣的是，尽管熵是一个状态量，但是其计算依赖于这个过程一定要是一个可逆过程。否则这个公式就不能应用。比如我们在计算气体自由膨胀的时候，这个式子就不能用了，需要我们将这个过程转换为一个等温膨胀才能够使用。

所以我们又提出了玻尔兹曼关系作为补充，有

$$S = k\ln W$$

其中 $W$ 是系统所包含的微观状态数，被称为热力学概率。