第一次:无理数
当时人们发现,有些数,比如 ,是没有办法表示成分数的。这一点用反证法可以得到很轻松的证明。
这次危机导致了,人们对于“数”和“形”的认知开始变得割裂了。因为 是可以用图形表示的(等腰直角三角形的底),但是没有办法用有理数来表示。也就是说,“数的集合”是小于“形的集合”的。所以人们开始研究几何,而对于代数的研究就放松了。
后来这个问题通过引入“无理数”解决了,无理数集就和形状可以对应了。但是“无理数”本身的定义,其实也很难。我个人觉得它依然借助了“形”。也就是说,无理数是将数轴分成两半的一个“划分”,这个划分满足一定的“无限特性”。
第二次:无穷小
在微积分中,出现了无穷小量,而这个无穷小量,有的时候是可以忽略的,而有的时候又是不可以忽略的,也就是“贝克莱悖论”:
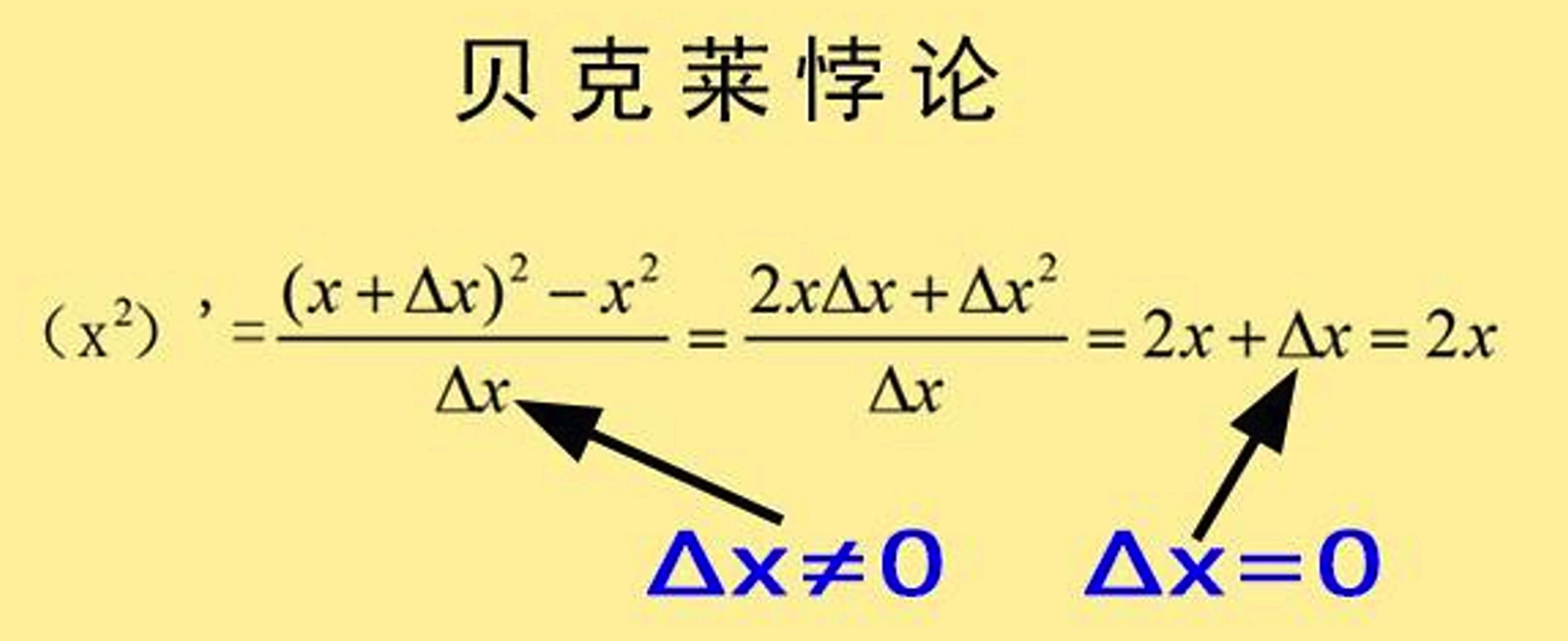
后来人们发明了 语言来规范化“极限”的表述。
第三次:集合论
在数学发展到一定阶段后,人们决定用集合论来作为“原初公理”,重新构建一遍数学体系。人们选择集合论,是因为它在数学上本质且优雅,表达能力强。
但是后来人们发现集合论本身存在问题,也就是“罗素悖论”,也可以理解为,集合是不能自指的,自指就会变成“递归死循环”。后来哥德尔彻底证明了集合论的问题并不可弥补(之前人们还打算把罗素悖论涉及到的这种集合剔除掉,然后再鸵鸟般的过日子呢),也就是哥德尔不完备定理。
直到现在,人们只能放弃用集合论来构建完整数学体系的尝试,而是转而去构建一些片面小巧,但是自洽的数学体系。
总结
我在知乎上看到一个说法,是说“三次危机”其实是中国特供故事,在西方并没有这种明确的划分。之所以是中国特供,是因为这种故事符合 Dialectics 中的“正反合”逻辑:先是有一个已经很完美的数学大厦了;然后人们突然发现了一个纰漏,使得这个大厦倒塌了;但是人们通过努力,修补了这个纰漏,建立起一个新的更好的数学大厦。